第六章 特殊平行四边形 综合练习(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 综合练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:44:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
综合练习
一、选择题
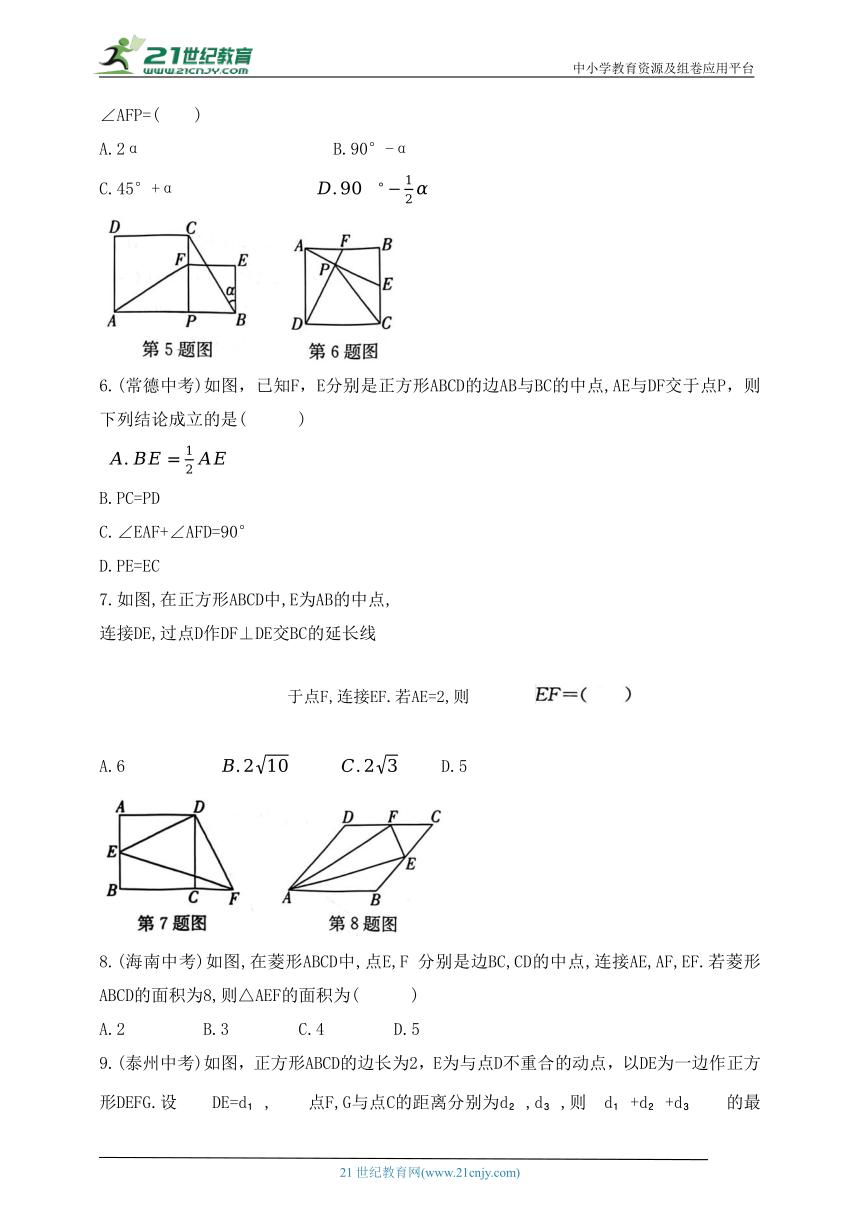
1.(自贡中考)如图,菱形ABCD的对角线交点与坐标原点O重合,点A(-2,5),则点C的坐标是( )
A.( 5,-2) B.( 2,-5)
C.( 2,5) D.( -2,-5)
2.(安徽中考)两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45°
C.180°-α D.270°-α
3.(淄博张店区模拟)如图,在菱形ABCD中,∠A=60°,AD=8,P是AB边上的一点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.8 C.4
4.(济南历城区模拟)如图,矩形ABCD中,点F 是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=15°,则∠ACF的度数是( )
A.15° B.20° C.30° D.45°
5.(泰州中考)如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则
∠AFP=( )
A.2α B.90°-α
C.45°+α
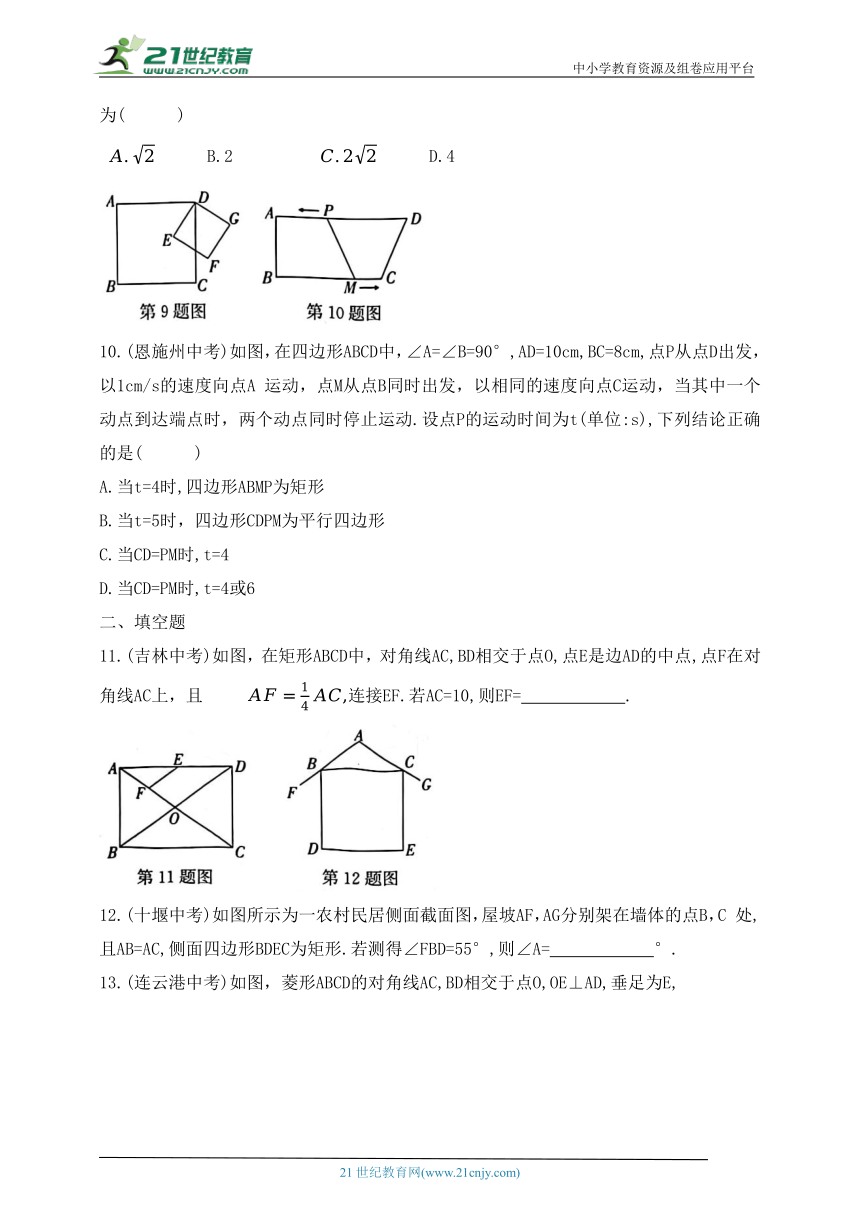
6.(常德中考)如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )
B.PC=PD
C.∠EAF+∠AFD=90°
D.PE=EC
7.如图,在正方形ABCD中,E为AB的中点,
连接DE,过点D作DF⊥DE交BC的延长线
A.6 D.5
8.(海南中考)如图,在菱形ABCD中,点E,F 分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2 B.3 C.4 D.5
9.(泰州中考)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设 DE=d , 点F,G与点C的距离分别为d ,d ,则 d +d +d 的最小值
为( )
B.2 D.4
10.(恩施州中考)如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A 运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当t=4时,四边形ABMP为矩形
B.当t=5时,四边形CDPM为平行四边形
C.当CD=PM时,t=4
D.当CD=PM时,t=4或6
二、填空题
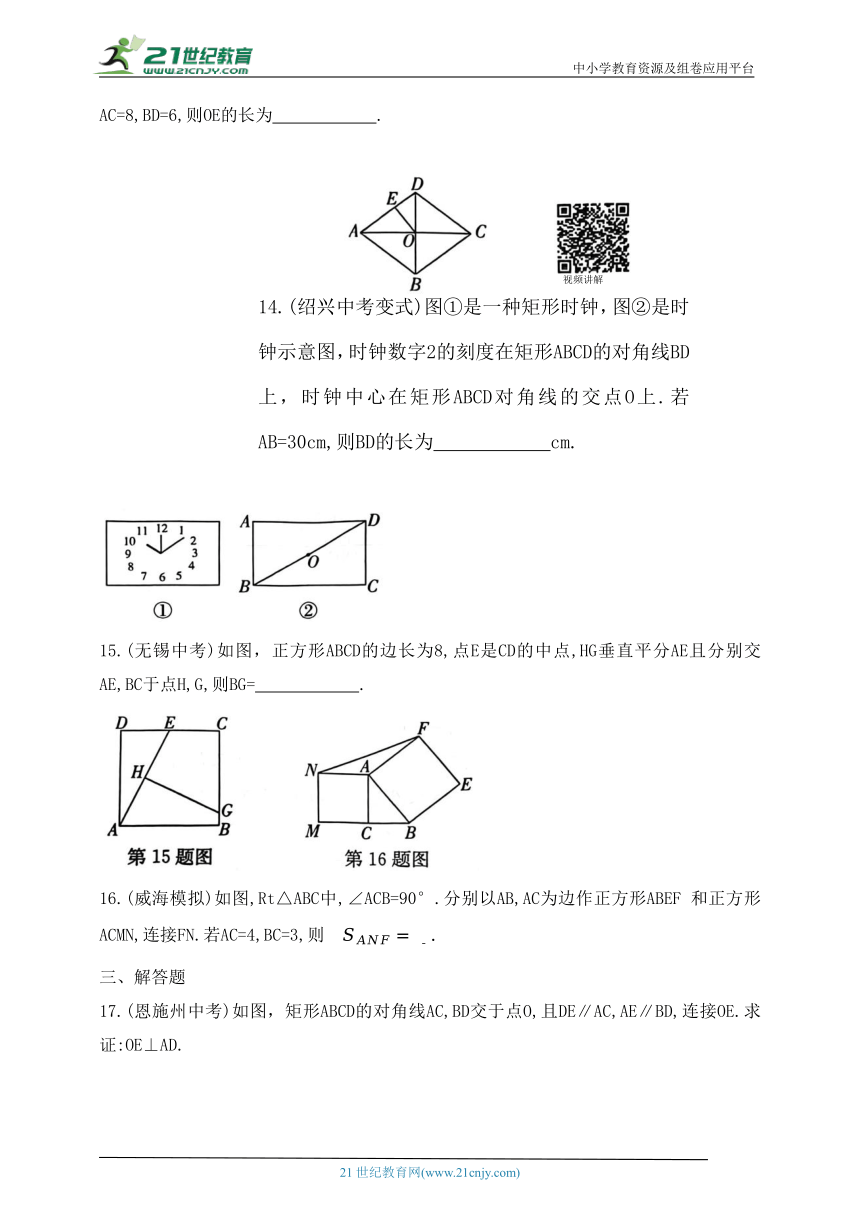
11.(吉林中考)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且 连接EF.若AC=10,则EF= .
12.(十堰中考)如图所示为一农村民居侧面截面图,屋坡AF,AG分别架在墙体的点B,C 处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FBD=55°,则∠A= °.
13.(连云港中考)如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为E,
AC=8,BD=6,则OE的长为 .
15.(无锡中考)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG= .
16.(威海模拟)如图,Rt△ABC中,∠ACB=90°.分别以AB,AC为边作正方形ABEF 和正方形ACMN,连接FN.若AC=4,BC=3,则
三、解答题
17.(恩施州中考)如图,矩形ABCD的对角线AC,BD交于点O,且DE∥AC,AE∥BD,连接OE.求证:OE⊥AD.
18.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
19.(南充中考)如图,在菱形ABCD中,点E,F 分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
(1)求证:△ADE≌△CDF.
(2)求证:ME=NF.
20.(泰州中考)如图,线段DE与AF分别为△ABC的中位线与中线.
(1)求证:AF与DE互相平分.
(2)当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形 请说明理由.
21.(丽水中考)如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF.
(2)若CD=4cm,EF=5cm,求BC的长.
22.(泰安中考)已知四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC,如图①,求证:四边形BECD为平行四边形.
(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图②,求证:△DGF 是等腰直角三角形.
23.(哈尔滨中考)已知矩形ABCD的对角线AC,BD相交于点O,点E是边AD上一点,连接BE,CE,OE,且BE=CE.
(1)如图①,求证:△BEO≌△CEO.
(2)如图②,设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图②中的四个三角形(△AEF除外),使写出的每个三角形的面积都与△AEF的面积相等.
1.B 2.C 3.C 4.C 5.B 6.C 7.B
8.B [解析]如图,连接AC,BD交于点O,AC交EF于点
G.∵四边形ABCD是菱形,∴AO=OC,菱形ABCD的面
积为 点E,F分别是边BC,CD的中点,
a,BD=b,则 即
9.C [解析]如图,连接AE.∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG.∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d +d +d =EF+CF+AE,∴点A,E,F,C在同一条直线上时,EF+CF+AE的值最小,即 d +d +d 的值最小.如图,连接AC,则 d +d +d 的最小值为AC.在Rt△ABC中,AC 的最小值为
10.D [解析]根据题意可得:DP=t,BM=t.∵AD=10cm,BC=8cm,∴AP=10-t,CM=8-t.当四边形ABMP为矩形时,AP=BM,即10-t=t,解得t=5,故A错误.当四边形CDPM为平行四边形时,DP=CM,即
t=8-t,解得t=4,故B错误,当CD=PM时,分两种情况.①四边形CDPM是平行四边形,此时CM=PD,即8-t=t,解得t=4.②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,则∠MGP=∠CHD=90°.∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD.∵AG=AP+ t.解得t=6.因此,当CD=PM时,t=4或6.故C错误,D正确.
12.110 14.60
15.1 [解析]如图,连接AG,EG.∵E是CD的中点,∴DE =CE=4.设CG=x,则BG=8-x.∵HG垂直平分AE,∴AG=EG.在Rt△ABG和Rt△GCE中,根据勾股定理得AB +BG =CE +CG , 即 8 +(8-x) =4 +x , 解得x=7,∴BG=BC-CG=8-7=1.
16.6 [解析]如图,过点F作FH⊥AH,交NA的延长线于
×4×3=6.
17.证明:∵DE∥AC,AE∥BD,∴四边形AODE为平行四边形.∵四边形ABCD为矩形,∴OA=OD,∴四边形AODE为菱形,∴OE⊥AD.
18.证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°.∵CE⊥BG,DF⊥CE,∴∠BEC=∠CFD=90°,∴∠BCE+∠CBE=90°=∠BCE+∠DCF,∴∠CBE=
∠DCF.在△CBE和△DCF中, ∴△CBE≌△DCF(AAS),∴CF=BE,CE=DF.∵CE =EF+CF,∴DF=BE+EF.
19.证明:(1)∵四边形ABCD是菱形,∴DA=DC,∠DAE
=∠DCF,AB=CB.∵BE=BF,∴AE=CF.在△ADE
20.(1)证明:∵点D是AB的中点, ∵点E 是AC的中点,点F是BC的中点,∴EF是△ABC的中位线, 四边形ADFE是平行四边形,∴AF与DE互相平分.
(2)解:当 时,四边形ADFE为矩形.理由:∵线段DE为△ABC的中位线. 由(1)得四边形ADFE是平行四边形,∴四边形ADFE为矩形.
21.(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=∠B=∠C=90°,AB=CD.由折叠得AB=PD,∠A=∠P=90°,∠B=∠PDF=90°,∴PD=CD.∵∠PDF=∠ADC,∴∠PDE=∠CDF.在△PDE和△CDF中,
(2)解:如图,过点E作EG⊥BC于点G,则∠EGF=90°,EG=CD=4.在Rt△EGF中,由勾股定理得FG= 设CF=x,则由(1)知PE=AE=BG=x.∵AD∥BC,∴∠DEF=∠BFE.由折叠得∠BFE=∠DFE,∴∠DEF=∠DFE,∴DE=DF=x+3.在Rt△CDF中,由勾股定理得DF =CD +CF , 即x +4 =
( x+ 3) ,解得
22.证明:(1)∵四边形ABCD为矩形,∴AB∥CD,AB=CD,CB⊥AE.又∵AC=EC,∴AB=BE,∴BE=CD,BE∥CD,∴四边形BECD为平行四边形.(2)∵AB=AD,∴矩形ABCD是正方形.∵EG⊥AC,∴∠E=∠GAE=∠GAD=45°,∴GE=GA.又∵AF=BE,∴AB=FE,
∴FE=AD.在△EGF和△AGD中,
∴△EGF≌△AGD(SAS),∴GF=GD,∠DGA =∠FGE,∴∠DGF=∠DGA+∠AGF=∠FGE+∠AGF =∠AGE=90°,∴△DGF是等腰直角三角形.
23.(1)证明:∵四边形ABCD是矩形, ∵BE=CE,OE=OE,∴△BEO≌△CEO(SSS).
(2)解:△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
综合练习
一、选择题
1.(自贡中考)如图,菱形ABCD的对角线交点与坐标原点O重合,点A(-2,5),则点C的坐标是( )
A.( 5,-2) B.( 2,-5)
C.( 2,5) D.( -2,-5)
2.(安徽中考)两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α-90° B.α-45°
C.180°-α D.270°-α
3.(淄博张店区模拟)如图,在菱形ABCD中,∠A=60°,AD=8,P是AB边上的一点,E,F分别是DP,BP的中点,则线段EF的长为( )
A.8 C.4
4.(济南历城区模拟)如图,矩形ABCD中,点F 是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=15°,则∠ACF的度数是( )
A.15° B.20° C.30° D.45°
5.(泰州中考)如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则
∠AFP=( )
A.2α B.90°-α
C.45°+α
6.(常德中考)如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )
B.PC=PD
C.∠EAF+∠AFD=90°
D.PE=EC
7.如图,在正方形ABCD中,E为AB的中点,
连接DE,过点D作DF⊥DE交BC的延长线
A.6 D.5
8.(海南中考)如图,在菱形ABCD中,点E,F 分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )
A.2 B.3 C.4 D.5
9.(泰州中考)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设 DE=d , 点F,G与点C的距离分别为d ,d ,则 d +d +d 的最小值
为( )
B.2 D.4
10.(恩施州中考)如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A 运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A.当t=4时,四边形ABMP为矩形
B.当t=5时,四边形CDPM为平行四边形
C.当CD=PM时,t=4
D.当CD=PM时,t=4或6
二、填空题
11.(吉林中考)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E是边AD的中点,点F在对角线AC上,且 连接EF.若AC=10,则EF= .
12.(十堰中考)如图所示为一农村民居侧面截面图,屋坡AF,AG分别架在墙体的点B,C 处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FBD=55°,则∠A= °.
13.(连云港中考)如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为E,
AC=8,BD=6,则OE的长为 .
15.(无锡中考)如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则BG= .
16.(威海模拟)如图,Rt△ABC中,∠ACB=90°.分别以AB,AC为边作正方形ABEF 和正方形ACMN,连接FN.若AC=4,BC=3,则
三、解答题
17.(恩施州中考)如图,矩形ABCD的对角线AC,BD交于点O,且DE∥AC,AE∥BD,连接OE.求证:OE⊥AD.
18.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
19.(南充中考)如图,在菱形ABCD中,点E,F 分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
(1)求证:△ADE≌△CDF.
(2)求证:ME=NF.
20.(泰州中考)如图,线段DE与AF分别为△ABC的中位线与中线.
(1)求证:AF与DE互相平分.
(2)当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形 请说明理由.
21.(丽水中考)如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF.
(2)若CD=4cm,EF=5cm,求BC的长.
22.(泰安中考)已知四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC,如图①,求证:四边形BECD为平行四边形.
(2)若AB=AD,点F是AB上的点,AF=BE,EG⊥AC于点G,如图②,求证:△DGF 是等腰直角三角形.
23.(哈尔滨中考)已知矩形ABCD的对角线AC,BD相交于点O,点E是边AD上一点,连接BE,CE,OE,且BE=CE.
(1)如图①,求证:△BEO≌△CEO.
(2)如图②,设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图②中的四个三角形(△AEF除外),使写出的每个三角形的面积都与△AEF的面积相等.
1.B 2.C 3.C 4.C 5.B 6.C 7.B
8.B [解析]如图,连接AC,BD交于点O,AC交EF于点
G.∵四边形ABCD是菱形,∴AO=OC,菱形ABCD的面
积为 点E,F分别是边BC,CD的中点,
a,BD=b,则 即
9.C [解析]如图,连接AE.∵四边形DEFG是正方形,∴∠EDG=90°,EF=DE=DG.∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴AE=CG,∴d +d +d =EF+CF+AE,∴点A,E,F,C在同一条直线上时,EF+CF+AE的值最小,即 d +d +d 的值最小.如图,连接AC,则 d +d +d 的最小值为AC.在Rt△ABC中,AC 的最小值为
10.D [解析]根据题意可得:DP=t,BM=t.∵AD=10cm,BC=8cm,∴AP=10-t,CM=8-t.当四边形ABMP为矩形时,AP=BM,即10-t=t,解得t=5,故A错误.当四边形CDPM为平行四边形时,DP=CM,即
t=8-t,解得t=4,故B错误,当CD=PM时,分两种情况.①四边形CDPM是平行四边形,此时CM=PD,即8-t=t,解得t=4.②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,则∠MGP=∠CHD=90°.∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD.∵AG=AP+ t.解得t=6.因此,当CD=PM时,t=4或6.故C错误,D正确.
12.110 14.60
15.1 [解析]如图,连接AG,EG.∵E是CD的中点,∴DE =CE=4.设CG=x,则BG=8-x.∵HG垂直平分AE,∴AG=EG.在Rt△ABG和Rt△GCE中,根据勾股定理得AB +BG =CE +CG , 即 8 +(8-x) =4 +x , 解得x=7,∴BG=BC-CG=8-7=1.
16.6 [解析]如图,过点F作FH⊥AH,交NA的延长线于
×4×3=6.
17.证明:∵DE∥AC,AE∥BD,∴四边形AODE为平行四边形.∵四边形ABCD为矩形,∴OA=OD,∴四边形AODE为菱形,∴OE⊥AD.
18.证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°.∵CE⊥BG,DF⊥CE,∴∠BEC=∠CFD=90°,∴∠BCE+∠CBE=90°=∠BCE+∠DCF,∴∠CBE=
∠DCF.在△CBE和△DCF中, ∴△CBE≌△DCF(AAS),∴CF=BE,CE=DF.∵CE =EF+CF,∴DF=BE+EF.
19.证明:(1)∵四边形ABCD是菱形,∴DA=DC,∠DAE
=∠DCF,AB=CB.∵BE=BF,∴AE=CF.在△ADE
20.(1)证明:∵点D是AB的中点, ∵点E 是AC的中点,点F是BC的中点,∴EF是△ABC的中位线, 四边形ADFE是平行四边形,∴AF与DE互相平分.
(2)解:当 时,四边形ADFE为矩形.理由:∵线段DE为△ABC的中位线. 由(1)得四边形ADFE是平行四边形,∴四边形ADFE为矩形.
21.(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=∠B=∠C=90°,AB=CD.由折叠得AB=PD,∠A=∠P=90°,∠B=∠PDF=90°,∴PD=CD.∵∠PDF=∠ADC,∴∠PDE=∠CDF.在△PDE和△CDF中,
(2)解:如图,过点E作EG⊥BC于点G,则∠EGF=90°,EG=CD=4.在Rt△EGF中,由勾股定理得FG= 设CF=x,则由(1)知PE=AE=BG=x.∵AD∥BC,∴∠DEF=∠BFE.由折叠得∠BFE=∠DFE,∴∠DEF=∠DFE,∴DE=DF=x+3.在Rt△CDF中,由勾股定理得DF =CD +CF , 即x +4 =
( x+ 3) ,解得
22.证明:(1)∵四边形ABCD为矩形,∴AB∥CD,AB=CD,CB⊥AE.又∵AC=EC,∴AB=BE,∴BE=CD,BE∥CD,∴四边形BECD为平行四边形.(2)∵AB=AD,∴矩形ABCD是正方形.∵EG⊥AC,∴∠E=∠GAE=∠GAD=45°,∴GE=GA.又∵AF=BE,∴AB=FE,
∴FE=AD.在△EGF和△AGD中,
∴△EGF≌△AGD(SAS),∴GF=GD,∠DGA =∠FGE,∴∠DGF=∠DGA+∠AGF=∠FGE+∠AGF =∠AGE=90°,∴△DGF是等腰直角三角形.
23.(1)证明:∵四边形ABCD是矩形, ∵BE=CE,OE=OE,∴△BEO≌△CEO(SSS).
(2)解:△DHE,△CHO,△DEG,△BFO都与△AEF的面积相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
