第六章《特殊平行四边形》检测题(含答案)
文档属性
| 名称 | 第六章《特殊平行四边形》检测题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
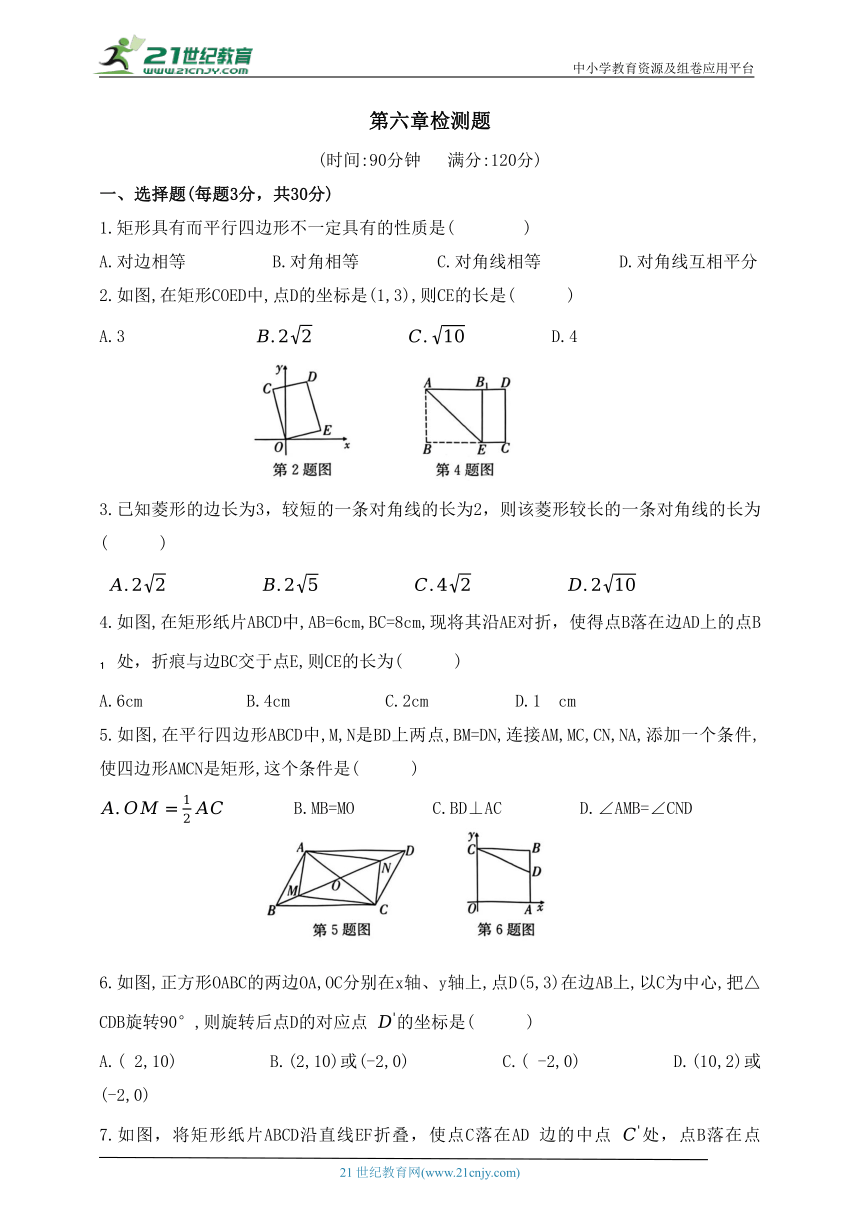
2.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A.3 D.4
3.已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
4.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B 处,折痕与边BC交于点E,则CE的长为( )
A.6cm B.4cm C.2cm D.1 cm
5.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
B.MB=MO C.BD⊥AC D.∠AMB=∠CND
6.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点 的坐标是( )
A.( 2,10) B.(2,10)或(-2,0) C.( -2,0) D.(10,2)或(-2,0)
7.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD 边的中点 处,点B落在点 处,其中AB=9,BC=6,则 的长为( )
B.4 C.4.5 D.5
8.如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到 当点 与点C重合时,点A与点 之间的距离为( )
A.6 B.8 C.10 D.12
9.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
10.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且EO=2DE,则AD的长为( )
C.10
二、填空题(每题3分,共30分)
11.木工师傅在做门窗时,不仅要用直尺测量两组对边的长度是否相等,还要测量它们的_________________是否也相等,以确保图形是矩形,其中包含的数学道理是 .
12.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
13.如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边的中点,若OH的长为2,则菱形ABCD的周长等于 .
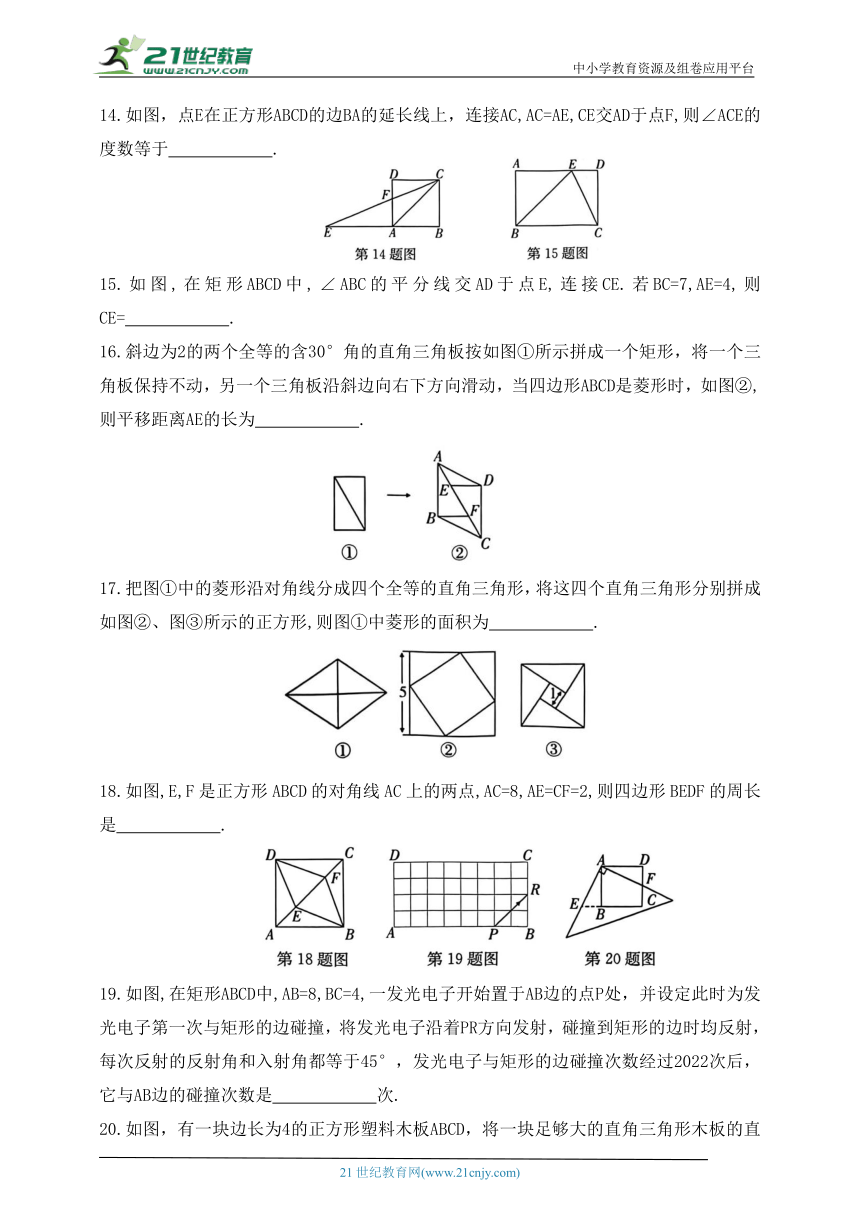
14.如图,点E在正方形ABCD的边BA的延长线上,连接AC,AC=AE,CE交AD于点F,则∠ACE的度数等于 .
15.如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE= .
16.斜边为2的两个全等的含30°角的直角三角板按如图①所示拼成一个矩形,将一个三角板保持不动,另一个三角板沿斜边向右下方向滑动,当四边形ABCD是菱形时,如图②,则平移距离AE的长为 .
17.把图①中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图②、图③所示的正方形,则图①中菱形的面积为 .
18.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
19.如图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,发光电子与矩形的边碰撞次数经过2022次后,它与AB边的碰撞次数是 次.
20.如图,有一块边长为4的正方形塑料木板ABCD,将一块足够大的直角三角形木板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
三、解答题(共60分)
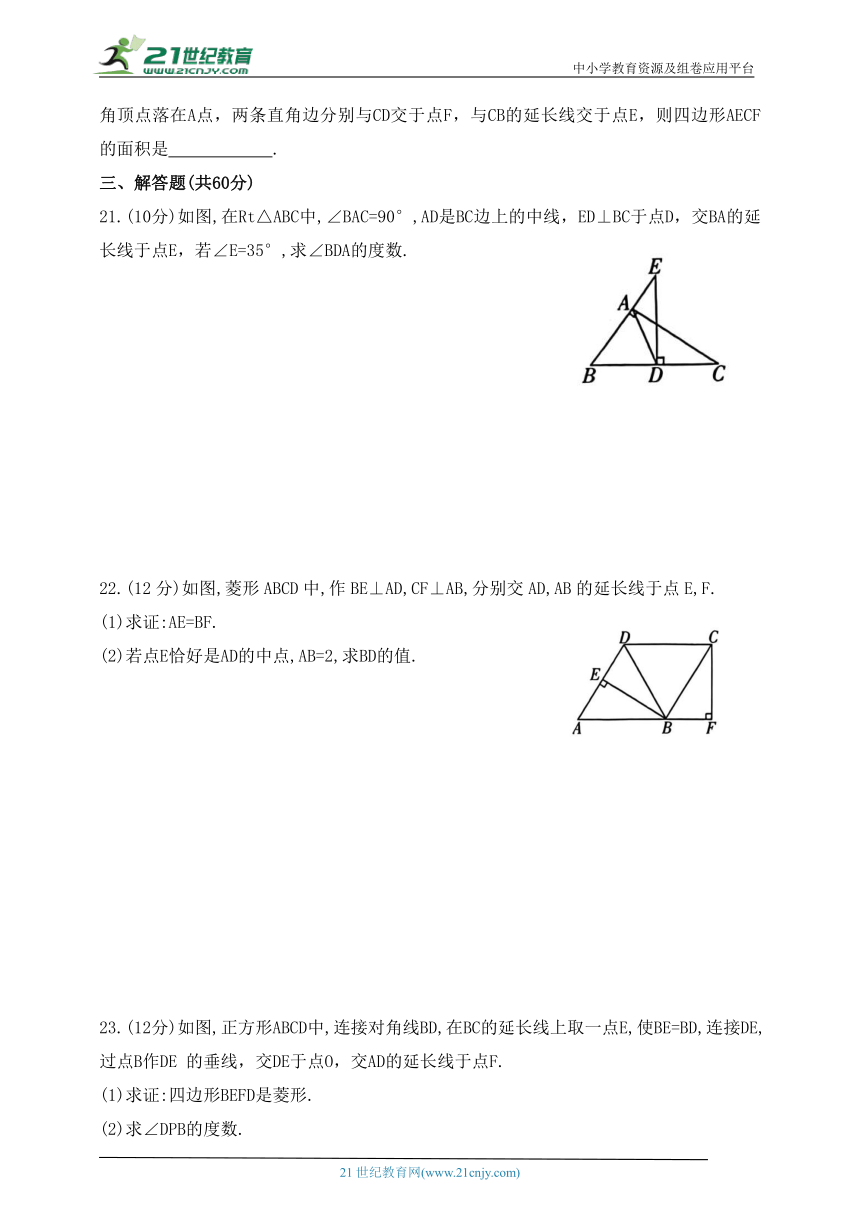
21.(10分)如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E,若∠E=35°,求∠BDA的度数.
22.(12分)如图,菱形ABCD中,作BE⊥AD,CF⊥AB,分别交AD,AB的延长线于点E,F.
(1)求证:AE=BF.
(2)若点E恰好是AD的中点,AB=2,求BD的值.
23.(12分)如图,正方形ABCD中,连接对角线BD,在BC的延长线上取一点E,使BE=BD,连接DE,过点B作DE 的垂线,交DE于点O,交AD的延长线于点F.
(1)求证:四边形BEFD是菱形.
(2)求∠DPB的度数.
24.(12分)如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰△ADE,且∠ADE=∠ABC,连接CE,过点E作EF∥BC,交CA的延长线于点F,连接BF.
(1)求证:∠ECA=∠ABC.
(2)若AF=AB,求证:四边形FBDE是矩形.
25.(14分)如图,正方形ABCD中,AB=8,点M为线段DC 上的动点,射线AM交BD于点E,交射线BC于点F,过点C作CQ⊥CE,交AF于点Q,
(1)求证:∠QCF=∠QFC.
(2)求证:△CMQ是等腰三角形.
(3)取DM的中点H,连接HQ,若HQ=5,求出BF 的长.
参考答案
1.C 2.C 3.C 4.C 5.A 6.B 7.D
8.C [解析]∵四边形ABCD是菱形,∴AC⊥BD,AO=OC
沿点A到点C的方向平移,得到点与点C重合,
9.D [解析]连接DE
∴矩形ECFG与正方形ABCD的面积相等.
10.A [解析]∵四边形ABCD是矩形,∴∠ADC=90°,BD
2DE,∴设DE=x,OE=2x,∴OD=OC=3x,AC=6x.
∵CE⊥BD,∴∠DEC=∠OEC=90°.
在Rt△OCE中,∵OE +CE =OC ,∴(2x) +5 =(3x) , 解得
∴∴
11.对角线 对角线相等的平行四边形是矩形
12.(4,4) 13.16 14.22.5° 15.5 16.1
17.12 [解析]如图所示,∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.
设OA=x,OB=y.由题意得 解得
∴菱形ABCD的面积
[解析]连接BD交AC于点O.
∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC.
∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF,∴四边形BEDF 为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,∴DE=DF=BE=BF.
∵AC=BD=8,∴OB=OD=
由勾股定理得DE=
∴四边形BEDF的周长
19.674 20.16
21.解:∵ED⊥BC,∠E=35°,∴∠B=55°.
∵在Rt△ABC 中,∠BAC=90°,AD是BC边上的中线,∴AD=BD,∴∠BAD=∠B=55°,
∴∠BDA=180°-∠B-∠BAD =70°.
22.(1)证明:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∴∠A=∠CBF.
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,∴△AEB≌△BFC(AAS),∴AE=BF.
(2)解:∵E是AD中点,且BE⊥AD,∴直线BE为AD的垂直平分线,∴BD=AB=2.
23.(1)证明:∵四边形ABCD是正方形,∴AD∥BC,∴∠FDO=∠DEB.
∵BD=BE,∴∠BDO=∠DEB,∴∠FDO=∠BDO.
∵BF⊥DE,∴∠BOD=90°=∠FOD.
又∵DO=DO,∴△BOD≌△FOD(ASA),∴DF=BD.
∵BD=BE,∴DF=BE.∵AD∥BC,即DF ∥BE,∴四边形BEFD是平行四边形,而BD=BE,
∴四边形BEFD是菱形.
(2)解:∵四边形ABCD是正方形,∴∠DBC=45°=∠BDC.
由(1)知四边形BEFD是菱形,
180°-∠DBO-∠BDC=112.5°.
24.证明:(1)∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°-2∠ABC.
同理,∠DAE=180°-2∠ADE.
∵∠ABC=∠ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE (SAS),∴∠ECA=∠ABC.
(2)∵∠ECA=∠ABC,∠ABC=∠ACB,∴∠ECF=∠ACB.
∵EF∥BC,∴∠EFC=∠ACB,∴∠EFC=∠ECF,∴EF=EC.
∵△ABD≌△ACE,∴BD=EC,∴BD=EF,∴四边形FBDE是平行四边形.
∵AF=AB=AC,∴∠AFB=∠ABF,∠ABC=∠ACB.
∵∠AFB+∠ABF+∠ABC +∠ACB=180°,∴∠ABF+∠ABC=90°,即∠CBF=90°,
∴四边形FBDE是矩形.
25.(1)证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE =∠CBE=45°.
∵BE=BE,∴△ABE≌△CBE(SAS),∴∠BAE=∠BCE.
∵∠ABC=90°,CQ⊥CE,∴∠QFC +BAE=90° ,∠QCF+∠BCE=90°,∴∠QCF =∠QFC.
(2)证明:∵四边形ABCD是正方形,∴∠DCB=∠DCF=90°,
∴∠MCQ+∠QCF=∠CMQ +∠QFC=90°,∴∠MCQ=∠CMQ,即QM=QC,
∴△CMQ是等腰三角形.
(3)解:如图,连接DF.
∵∠QCF=∠QFC,∴QC=QF.∵QM=QC,∴QF=QM.
∵H是DM的中点,∴QH是△MDF的中位线,∴DF=2HQ.
∵HQ=5,∴DF=10.
∵DC=BC=AB=
CF=8+6=14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
2.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A.3 D.4
3.已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
4.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B 处,折痕与边BC交于点E,则CE的长为( )
A.6cm B.4cm C.2cm D.1 cm
5.如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )
B.MB=MO C.BD⊥AC D.∠AMB=∠CND
6.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点 的坐标是( )
A.( 2,10) B.(2,10)或(-2,0) C.( -2,0) D.(10,2)或(-2,0)
7.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD 边的中点 处,点B落在点 处,其中AB=9,BC=6,则 的长为( )
B.4 C.4.5 D.5
8.如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到 当点 与点C重合时,点A与点 之间的距离为( )
A.6 B.8 C.10 D.12
9.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
10.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5,且EO=2DE,则AD的长为( )
C.10
二、填空题(每题3分,共30分)
11.木工师傅在做门窗时,不仅要用直尺测量两组对边的长度是否相等,还要测量它们的_________________是否也相等,以确保图形是矩形,其中包含的数学道理是 .
12.如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为 .
13.如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边的中点,若OH的长为2,则菱形ABCD的周长等于 .
14.如图,点E在正方形ABCD的边BA的延长线上,连接AC,AC=AE,CE交AD于点F,则∠ACE的度数等于 .
15.如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE= .
16.斜边为2的两个全等的含30°角的直角三角板按如图①所示拼成一个矩形,将一个三角板保持不动,另一个三角板沿斜边向右下方向滑动,当四边形ABCD是菱形时,如图②,则平移距离AE的长为 .
17.把图①中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图②、图③所示的正方形,则图①中菱形的面积为 .
18.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
19.如图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,发光电子与矩形的边碰撞次数经过2022次后,它与AB边的碰撞次数是 次.
20.如图,有一块边长为4的正方形塑料木板ABCD,将一块足够大的直角三角形木板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
三、解答题(共60分)
21.(10分)如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E,若∠E=35°,求∠BDA的度数.
22.(12分)如图,菱形ABCD中,作BE⊥AD,CF⊥AB,分别交AD,AB的延长线于点E,F.
(1)求证:AE=BF.
(2)若点E恰好是AD的中点,AB=2,求BD的值.
23.(12分)如图,正方形ABCD中,连接对角线BD,在BC的延长线上取一点E,使BE=BD,连接DE,过点B作DE 的垂线,交DE于点O,交AD的延长线于点F.
(1)求证:四边形BEFD是菱形.
(2)求∠DPB的度数.
24.(12分)如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰△ADE,且∠ADE=∠ABC,连接CE,过点E作EF∥BC,交CA的延长线于点F,连接BF.
(1)求证:∠ECA=∠ABC.
(2)若AF=AB,求证:四边形FBDE是矩形.
25.(14分)如图,正方形ABCD中,AB=8,点M为线段DC 上的动点,射线AM交BD于点E,交射线BC于点F,过点C作CQ⊥CE,交AF于点Q,
(1)求证:∠QCF=∠QFC.
(2)求证:△CMQ是等腰三角形.
(3)取DM的中点H,连接HQ,若HQ=5,求出BF 的长.
参考答案
1.C 2.C 3.C 4.C 5.A 6.B 7.D
8.C [解析]∵四边形ABCD是菱形,∴AC⊥BD,AO=OC
沿点A到点C的方向平移,得到点与点C重合,
9.D [解析]连接DE
∴矩形ECFG与正方形ABCD的面积相等.
10.A [解析]∵四边形ABCD是矩形,∴∠ADC=90°,BD
2DE,∴设DE=x,OE=2x,∴OD=OC=3x,AC=6x.
∵CE⊥BD,∴∠DEC=∠OEC=90°.
在Rt△OCE中,∵OE +CE =OC ,∴(2x) +5 =(3x) , 解得
∴∴
11.对角线 对角线相等的平行四边形是矩形
12.(4,4) 13.16 14.22.5° 15.5 16.1
17.12 [解析]如图所示,∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.
设OA=x,OB=y.由题意得 解得
∴菱形ABCD的面积
[解析]连接BD交AC于点O.
∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC.
∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF,∴四边形BEDF 为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,∴DE=DF=BE=BF.
∵AC=BD=8,∴OB=OD=
由勾股定理得DE=
∴四边形BEDF的周长
19.674 20.16
21.解:∵ED⊥BC,∠E=35°,∴∠B=55°.
∵在Rt△ABC 中,∠BAC=90°,AD是BC边上的中线,∴AD=BD,∴∠BAD=∠B=55°,
∴∠BDA=180°-∠B-∠BAD =70°.
22.(1)证明:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∴∠A=∠CBF.
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,∴△AEB≌△BFC(AAS),∴AE=BF.
(2)解:∵E是AD中点,且BE⊥AD,∴直线BE为AD的垂直平分线,∴BD=AB=2.
23.(1)证明:∵四边形ABCD是正方形,∴AD∥BC,∴∠FDO=∠DEB.
∵BD=BE,∴∠BDO=∠DEB,∴∠FDO=∠BDO.
∵BF⊥DE,∴∠BOD=90°=∠FOD.
又∵DO=DO,∴△BOD≌△FOD(ASA),∴DF=BD.
∵BD=BE,∴DF=BE.∵AD∥BC,即DF ∥BE,∴四边形BEFD是平行四边形,而BD=BE,
∴四边形BEFD是菱形.
(2)解:∵四边形ABCD是正方形,∴∠DBC=45°=∠BDC.
由(1)知四边形BEFD是菱形,
180°-∠DBO-∠BDC=112.5°.
24.证明:(1)∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°-2∠ABC.
同理,∠DAE=180°-2∠ADE.
∵∠ABC=∠ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE (SAS),∴∠ECA=∠ABC.
(2)∵∠ECA=∠ABC,∠ABC=∠ACB,∴∠ECF=∠ACB.
∵EF∥BC,∴∠EFC=∠ACB,∴∠EFC=∠ECF,∴EF=EC.
∵△ABD≌△ACE,∴BD=EC,∴BD=EF,∴四边形FBDE是平行四边形.
∵AF=AB=AC,∴∠AFB=∠ABF,∠ABC=∠ACB.
∵∠AFB+∠ABF+∠ABC +∠ACB=180°,∴∠ABF+∠ABC=90°,即∠CBF=90°,
∴四边形FBDE是矩形.
25.(1)证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE =∠CBE=45°.
∵BE=BE,∴△ABE≌△CBE(SAS),∴∠BAE=∠BCE.
∵∠ABC=90°,CQ⊥CE,∴∠QFC +BAE=90° ,∠QCF+∠BCE=90°,∴∠QCF =∠QFC.
(2)证明:∵四边形ABCD是正方形,∴∠DCB=∠DCF=90°,
∴∠MCQ+∠QCF=∠CMQ +∠QFC=90°,∴∠MCQ=∠CMQ,即QM=QC,
∴△CMQ是等腰三角形.
(3)解:如图,连接DF.
∵∠QCF=∠QFC,∴QC=QF.∵QM=QC,∴QF=QM.
∵H是DM的中点,∴QH是△MDF的中位线,∴DF=2HQ.
∵HQ=5,∴DF=10.
∵DC=BC=AB=
CF=8+6=14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
