【新课标】24.2.2垂径定理 课件(共39张PPT)
文档属性
| 名称 | 【新课标】24.2.2垂径定理 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
24.2.2垂径定理
沪科版 九年级下
教学内容分析
本节课在前面学习了圆的弦、弧、弓形、直径等基本概念的基础上,进一步学习垂直的直径平分弦的性质,并且学习垂径定理的推论。
教学目标
1.证明和理解垂径定理及其两个推论(重点)
2.运用垂径定理及其推论,解决圆与三角形、四边形的综合实际问题(难点)
核心素养分析
本节重点研究了垂直于弦的直径,平分弦的直径、平分弦所对的两条弧之间的关系,在证明垂径定理及其推论的过程中,培养了学生几何直观的观念,也提高了学生的计算能力。
新知导入
点P与圆心O的距离为d,半径为r,点与圆的位置关系如何用d和r的关系判断呢?
(1)点P在⊙O上 OP=r;
(2)点P在⊙O内 OP(3)点P在⊙O外 OP>r。
新知讲解
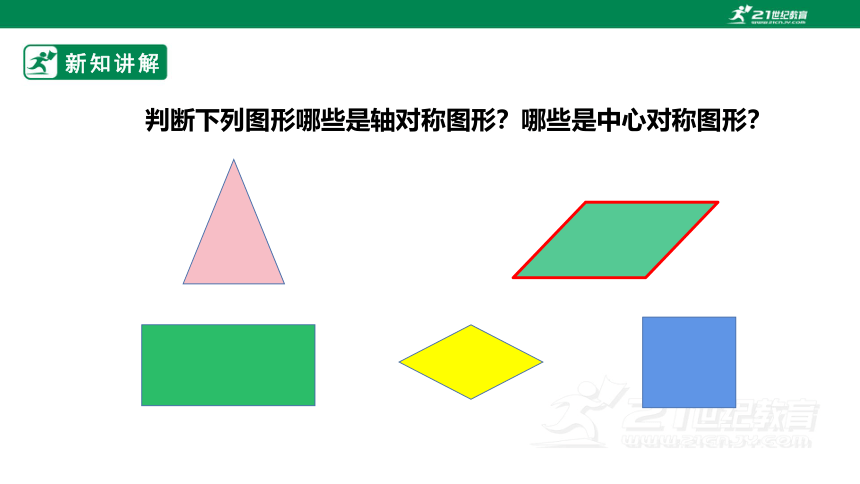
判断下列图形哪些是轴对称图形?哪些是中心对称图形?
新知讲解
轴对称图形:等腰三角形、矩形、菱形、正方形
中心对称图形:平行四边形、矩形、菱形、正方形
O
O
O
O
新知讲解
圆是否具有对称性呢 根据它的对称性又能推出圆的哪些性质呢
新知讲解
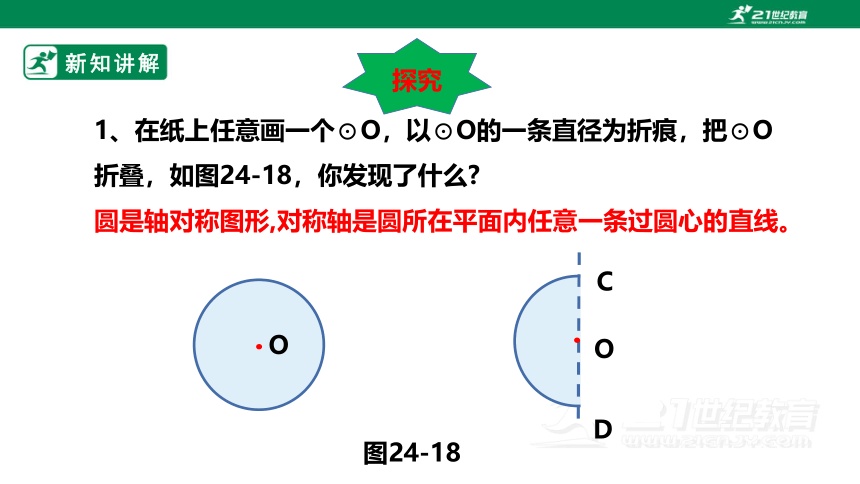
1、在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O
折叠,如图24-18,你发现了什么
圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线。
探究
图24-18
O
C
D
O
.
.
新知讲解
探究
图24-18
O
.
A(B)
C
D
.
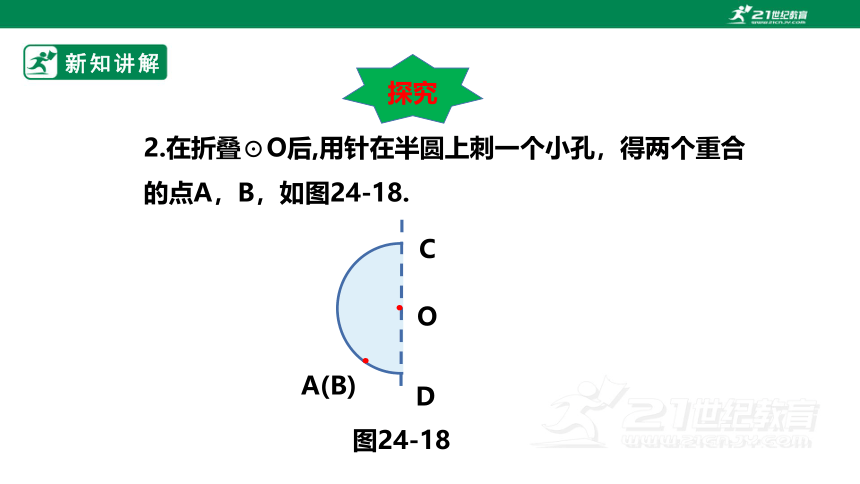
2.在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,如图24-18.
新知讲解
把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点.
图24-19
O
.
A
B
C
D
.
.
新知讲解
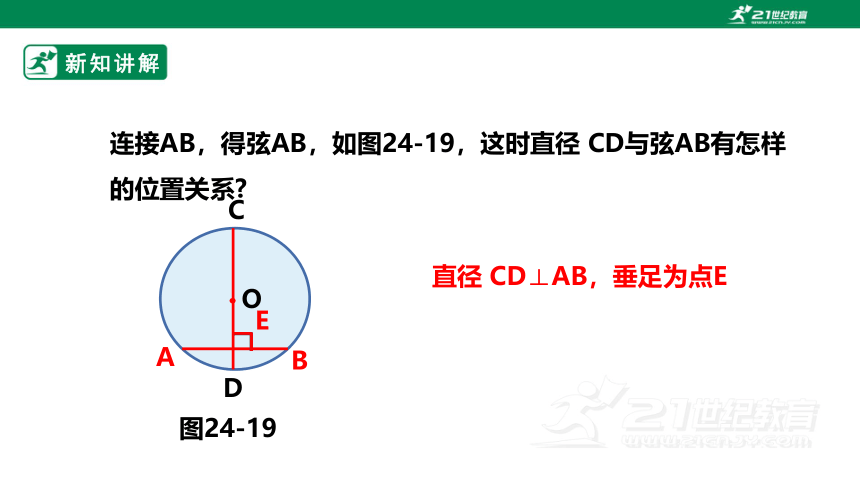
连接AB,得弦AB,如图24-19,这时直径 CD与弦AB有怎样的位置关系
图24-19
直径 CD⊥AB,垂足为点E
O
.
A
B
C
D
E
新知讲解
3.直径CD把劣弧 分成 与 两部分,把优弧 分成 与 两部分,这时 与 、 与 各有怎样的关系
⌒
AC
⌒
CB
⌒
AD
⌒
DB
⌒
ADB
⌒
AD
⌒
DB
⌒
ACB
⌒
AC
⌒
CB
图24-19
O
.
A
B
C
D
E
⌒
AD=
⌒
DB
⌒
AC=
⌒
CB
新知讲解
垂径定理:垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.
图24-19
O
.
A
B
C
D
E
即:AE= EB, = = .
⌒
AD
⌒
DB
⌒
AC
⌒
CB
新知讲解
已知:如图24-20,在⊙O中,CD是直径,AB是弦,并且CD⊥AB,垂足为E.
求证: AE= EB, = (或 = ).
图24-20
⌒
AD
⌒
DB
⌒
AC
⌒
CB
新知讲解
证明:连接OA,OB,则OA =OB,
△OAB为等腰三角形,
所以底边AB上的高OE所在直线CD是AB的垂直平分线,
因此点A与点B关于直线CD对称.
新知讲解
因此,AE=BE, = , =
⌒
AD
⌒
DB
⌒
AC
⌒
CB
同理,如果点P是⊙O上任意一点,过点P作直线
CD的垂线,与⊙O相交于点Q,
则点P与点Q关于直线CD也对称,
所以⊙O关于直线CD对称.当把圆沿着直径CD折叠时,
CD两侧的两个半圆重合,AE与BE重合,点A与点B重合,
与 重合, 与 重合.
⌒
AD
⌒
DB
⌒
AC
⌒
CB
P
Q
新知讲解
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
新知讲解
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其他三个结论。
O
.
A
B
C
D
E
判断下列命题是否正确:
1、平分一条直径的弦必垂直于这条直径( )
2、平分一条弧的直线垂直于这条弧所对的弦( )
3、弦的垂线必经过这条弦所在圆的圆心( )
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心( )
新知讲解
×
×
×
√
解:1、两条直径互相平分,但不一定垂直,错误;
2、平分一条弧的直线不一定垂直于这条弧所对的弦,错误;
3、弦的垂直平分线必经过这条弦所在圆的圆心,错误;
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心,正确。
新知讲解
例2、如图24-21,⊙O的半径为5cm,弦AB为6cm,求圆心O到弦AB的距离。
新知讲解
┓
O
A
B
图24-21
E
圆心到弦的距离叫做弦心距.
新知讲解
解:连接OA,过圆心O作OE⊥AB,垂足为E,则
AE=EB= AB = ×6= 3(cm).
又∵OA =5 cm,
在Rt△OEA中,
有
=4(cm).
答.圆心O到弦AB的距离是4cm.
┓
A
图24-21
E
O
新知讲解
例3 赵州桥(图24-22)建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆孤形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 求赵州桥桥拱所在圆
的半径(精确到0.1m)
图24-22
新知讲解
解:如图24-23,
过桥拱所在圆的圆心O作AB的垂线,
交 于点C,交AB于点D,
则CD=7.2 m.
由垂径定理,得
AD= AB = ×37.4 =18.7( m ).
⌒
AB
图24-23
D
A
B
C
37.4 单位m
7.2
O
新知讲解
设⊙O的半径为Rm,
在Rt△AOD中,
AO=R,OD=R-7.2,AD = 18.7.
由勾股定理,得
AO2= OD2+AD2.
∴R2=(R-7.2)2+18.72.
解方程,得 R≈27.9.
答:赵州桥桥拱所在圆的半径约为27.9m.
图24-23
D
A
B
C
37.4 单位m
7.2
O
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则OE=( )
A. 8cm B. 5cm C. 3cm D. 2cm
课堂练习
C
解:∵CD⊥AB,
∴CE=DE= CD= ×8=4,
在Rt△OCE中,OE=
=3(cm).
故选:C.
课堂练习
课堂练习
2.京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮主视图的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的
一圈中最佳观景的时长为_____分钟.
课堂练习
解:摩天轮转动的角速度为:360°÷18分=20°/分,
由题意得:AD⊥PE,AD=88米,AC=100米,CE=PQ=34米,则OP=OD=44(米),DC=AC-AD=12(米),
∴ED=EC-DC=34-12=22(米),
∴OE=OD-ED=22(米),
∴OE= OP,
∵∠OEP=90°,
课堂练习
∴∠OPE=30°,
∴∠POE=90°-30°=60°,
∴∠AOP=180°-∠BOC=120°,
∴最佳观赏位置的圆心角为2×120°=240°,
∴在运行的一圈里最佳观赏时长为:
240°÷20°/分=12(分钟),
故答案为:12.
课堂练习
3.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),
课堂练习
求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,
cos41.3°≈0.75,tan41.3°≈0.88)
解:连接CO并延长,与AB交于点D,
∵CD⊥AB,
∴AD=BD= AB=3(米),
在Rt△AOD中,∠OAB=41.3°,
∴ ,
即 (米)
课堂练习
OD=AD tan41.3°≈3×0.88=2.64(米),
则CD=CO+OD=4+2.64=6.64(米).
∴点C到弦AB所在直线的距离约为6.64米.
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其他三个结论。
O
.
A
B
C
D
E
课堂总结
板书设计
24.2.2 垂径定理
1.垂径定理及其推论
2.例2
例3
作业布置
必做题:课本P17的第1~2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.2.2垂径定理
沪科版 九年级下
教学内容分析
本节课在前面学习了圆的弦、弧、弓形、直径等基本概念的基础上,进一步学习垂直的直径平分弦的性质,并且学习垂径定理的推论。
教学目标
1.证明和理解垂径定理及其两个推论(重点)
2.运用垂径定理及其推论,解决圆与三角形、四边形的综合实际问题(难点)
核心素养分析
本节重点研究了垂直于弦的直径,平分弦的直径、平分弦所对的两条弧之间的关系,在证明垂径定理及其推论的过程中,培养了学生几何直观的观念,也提高了学生的计算能力。
新知导入
点P与圆心O的距离为d,半径为r,点与圆的位置关系如何用d和r的关系判断呢?
(1)点P在⊙O上 OP=r;
(2)点P在⊙O内 OP
新知讲解
判断下列图形哪些是轴对称图形?哪些是中心对称图形?
新知讲解
轴对称图形:等腰三角形、矩形、菱形、正方形
中心对称图形:平行四边形、矩形、菱形、正方形
O
O
O
O
新知讲解
圆是否具有对称性呢 根据它的对称性又能推出圆的哪些性质呢
新知讲解
1、在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O
折叠,如图24-18,你发现了什么
圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线。
探究
图24-18
O
C
D
O
.
.
新知讲解
探究
图24-18
O
.
A(B)
C
D
.
2.在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,如图24-18.
新知讲解
把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点.
图24-19
O
.
A
B
C
D
.
.
新知讲解
连接AB,得弦AB,如图24-19,这时直径 CD与弦AB有怎样的位置关系
图24-19
直径 CD⊥AB,垂足为点E
O
.
A
B
C
D
E
新知讲解
3.直径CD把劣弧 分成 与 两部分,把优弧 分成 与 两部分,这时 与 、 与 各有怎样的关系
⌒
AC
⌒
CB
⌒
AD
⌒
DB
⌒
ADB
⌒
AD
⌒
DB
⌒
ACB
⌒
AC
⌒
CB
图24-19
O
.
A
B
C
D
E
⌒
AD=
⌒
DB
⌒
AC=
⌒
CB
新知讲解
垂径定理:垂直于弦的直径平分这条弦,
并且平分这条弦所对的两条弧.
图24-19
O
.
A
B
C
D
E
即:AE= EB, = = .
⌒
AD
⌒
DB
⌒
AC
⌒
CB
新知讲解
已知:如图24-20,在⊙O中,CD是直径,AB是弦,并且CD⊥AB,垂足为E.
求证: AE= EB, = (或 = ).
图24-20
⌒
AD
⌒
DB
⌒
AC
⌒
CB
新知讲解
证明:连接OA,OB,则OA =OB,
△OAB为等腰三角形,
所以底边AB上的高OE所在直线CD是AB的垂直平分线,
因此点A与点B关于直线CD对称.
新知讲解
因此,AE=BE, = , =
⌒
AD
⌒
DB
⌒
AC
⌒
CB
同理,如果点P是⊙O上任意一点,过点P作直线
CD的垂线,与⊙O相交于点Q,
则点P与点Q关于直线CD也对称,
所以⊙O关于直线CD对称.当把圆沿着直径CD折叠时,
CD两侧的两个半圆重合,AE与BE重合,点A与点B重合,
与 重合, 与 重合.
⌒
AD
⌒
DB
⌒
AC
⌒
CB
P
Q
新知讲解
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
新知讲解
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其他三个结论。
O
.
A
B
C
D
E
判断下列命题是否正确:
1、平分一条直径的弦必垂直于这条直径( )
2、平分一条弧的直线垂直于这条弧所对的弦( )
3、弦的垂线必经过这条弦所在圆的圆心( )
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心( )
新知讲解
×
×
×
√
解:1、两条直径互相平分,但不一定垂直,错误;
2、平分一条弧的直线不一定垂直于这条弧所对的弦,错误;
3、弦的垂直平分线必经过这条弦所在圆的圆心,错误;
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心,正确。
新知讲解
例2、如图24-21,⊙O的半径为5cm,弦AB为6cm,求圆心O到弦AB的距离。
新知讲解
┓
O
A
B
图24-21
E
圆心到弦的距离叫做弦心距.
新知讲解
解:连接OA,过圆心O作OE⊥AB,垂足为E,则
AE=EB= AB = ×6= 3(cm).
又∵OA =5 cm,
在Rt△OEA中,
有
=4(cm).
答.圆心O到弦AB的距离是4cm.
┓
A
图24-21
E
O
新知讲解
例3 赵州桥(图24-22)建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆孤形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 求赵州桥桥拱所在圆
的半径(精确到0.1m)
图24-22
新知讲解
解:如图24-23,
过桥拱所在圆的圆心O作AB的垂线,
交 于点C,交AB于点D,
则CD=7.2 m.
由垂径定理,得
AD= AB = ×37.4 =18.7( m ).
⌒
AB
图24-23
D
A
B
C
37.4 单位m
7.2
O
新知讲解
设⊙O的半径为Rm,
在Rt△AOD中,
AO=R,OD=R-7.2,AD = 18.7.
由勾股定理,得
AO2= OD2+AD2.
∴R2=(R-7.2)2+18.72.
解方程,得 R≈27.9.
答:赵州桥桥拱所在圆的半径约为27.9m.
图24-23
D
A
B
C
37.4 单位m
7.2
O
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则OE=( )
A. 8cm B. 5cm C. 3cm D. 2cm
课堂练习
C
解:∵CD⊥AB,
∴CE=DE= CD= ×8=4,
在Rt△OCE中,OE=
=3(cm).
故选:C.
课堂练习
课堂练习
2.京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮主视图的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的
一圈中最佳观景的时长为_____分钟.
课堂练习
解:摩天轮转动的角速度为:360°÷18分=20°/分,
由题意得:AD⊥PE,AD=88米,AC=100米,CE=PQ=34米,则OP=OD=44(米),DC=AC-AD=12(米),
∴ED=EC-DC=34-12=22(米),
∴OE=OD-ED=22(米),
∴OE= OP,
∵∠OEP=90°,
课堂练习
∴∠OPE=30°,
∴∠POE=90°-30°=60°,
∴∠AOP=180°-∠BOC=120°,
∴最佳观赏位置的圆心角为2×120°=240°,
∴在运行的一圈里最佳观赏时长为:
240°÷20°/分=12(分钟),
故答案为:12.
课堂练习
3.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),
课堂练习
求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,
cos41.3°≈0.75,tan41.3°≈0.88)
解:连接CO并延长,与AB交于点D,
∵CD⊥AB,
∴AD=BD= AB=3(米),
在Rt△AOD中,∠OAB=41.3°,
∴ ,
即 (米)
课堂练习
OD=AD tan41.3°≈3×0.88=2.64(米),
则CD=CO+OD=4+2.64=6.64(米).
∴点C到弦AB所在直线的距离约为6.64米.
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其他三个结论。
O
.
A
B
C
D
E
课堂总结
板书设计
24.2.2 垂径定理
1.垂径定理及其推论
2.例2
例3
作业布置
必做题:课本P17的第1~2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
