2.4.1二次函数的应用——最大(小)面积问题 课件(共21张PPT)
文档属性
| 名称 | 2.4.1二次函数的应用——最大(小)面积问题 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
2.4.1二次函数的应用——最大(小)面积问题
北师大版 九年级 下册
教学目标
教学目标:1、根据实际问题分析变量之间的关系,再由变量关系得到二次函数的关系式;
2、会利用二次函数的关系式,通过配方法求出实际问题的最大值或最小值,记住最值一定要符合实际问题的具体要求;
3、会利用二次函数求出图形几何问题中的面积最大值问题;教学重点:
教学难点:学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
新知讲解
合作学习
①当a>0时,y有最小值=
②当a<0时,y有最大值=
二次函数的最值求法
合作学习
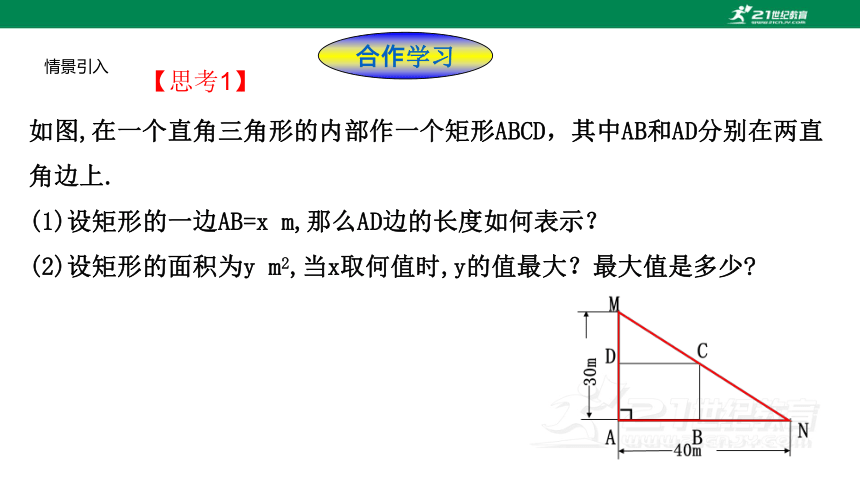
【思考1】
情景引入
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=x m,那么AD边的长度如何表示?
(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少
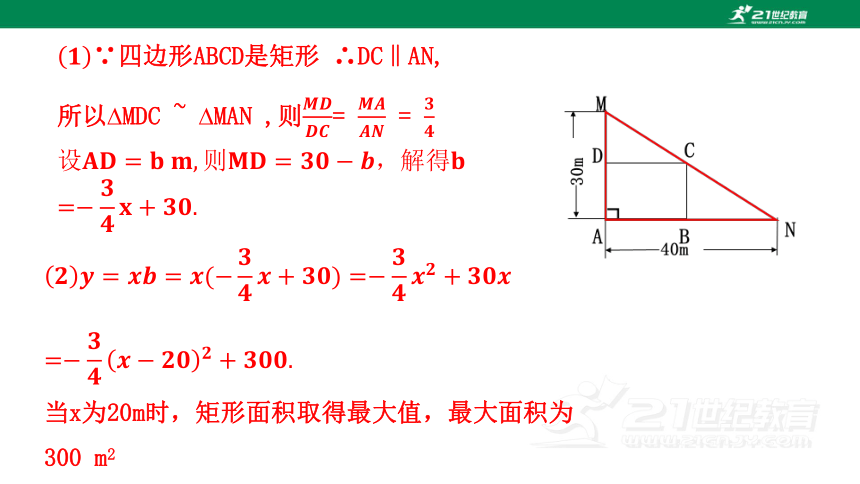
∵四边形ABCD是矩形 ∴DC‖AN,
所以 MDC ~ MAN ,则= =
当x为20m时,矩形面积取得最大值,最大面积为300 m2
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.设矩形的一边AF=x m, 设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少
【思考2】
提炼概念
利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且
用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
典例精讲
某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
【例题】
解析:
即当x=1.07m时,窗户通过的光线最多.此时窗户的面积为4.02m2.
归纳概念
【小结】解决几何图形面积的最值问题的基本步骤:
1.确定面积的变化与哪些量的变化有关;
2.利用图形的面积与这些变量之间的关系建立二次函数的模型;
3.利用二次函数的性质以及自变量的取值范围确定面积的最大值或最小值.
课堂练习
1. 把一根长的铁丝分成两段,每一段弯曲成一个正方形,面积和最小是( )
A. B. C. D.
2.用总长为a米的材料做成如图1所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图2,则a的值是( )
A.16 B.12 C.8 D.4
【答案】B
【分析】因为x=2时,面积最大,为4,根据图形是矩形,由面积公式易得长为2米,从而得出a的值.
【详解】解:由图象可知,当x=2时,y有最大,最大值为4,
∴当x=2米,窗框的最大面积是4平方米,
根据矩形面积计算公式,矩形的长为4÷2=2(米),
∴材料总长a=2×3+2×3=12(米).
故选:B.
3.已知,一个铝合金窗框如图所示,所使用的铝合金材料长度为18cm.设AB长为xm,窗户的总面积为Sm2.
(1)求S关于x的函数表达式.
(2)若AB的长不能低于2m,且AB<BC,求此时窗户总面积S的最大值和最小值.
【答案】(1)S=-+9x
(2)窗户总面积S的最大值m2,最小值是12m2
【分析】(1)根据题意和图形可以求得S与x的函数表达式;
(2)根据题意可以得到关于x的不等式,从而求出x的范围,然后根据(1)中的函数解析式和二次函数的性质即可解答.
3
课堂总结
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.4.1二次函数的应用——最大(小)面积问题
北师大版 九年级 下册
教学目标
教学目标:1、根据实际问题分析变量之间的关系,再由变量关系得到二次函数的关系式;
2、会利用二次函数的关系式,通过配方法求出实际问题的最大值或最小值,记住最值一定要符合实际问题的具体要求;
3、会利用二次函数求出图形几何问题中的面积最大值问题;教学重点:
教学难点:学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
新知讲解
合作学习
①当a>0时,y有最小值=
②当a<0时,y有最大值=
二次函数的最值求法
合作学习
【思考1】
情景引入
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=x m,那么AD边的长度如何表示?
(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少
∵四边形ABCD是矩形 ∴DC‖AN,
所以 MDC ~ MAN ,则= =
当x为20m时,矩形面积取得最大值,最大面积为300 m2
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.设矩形的一边AF=x m, 设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少
【思考2】
提炼概念
利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且
用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
典例精讲
某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m) 此时,窗户的面积是多少
【例题】
解析:
即当x=1.07m时,窗户通过的光线最多.此时窗户的面积为4.02m2.
归纳概念
【小结】解决几何图形面积的最值问题的基本步骤:
1.确定面积的变化与哪些量的变化有关;
2.利用图形的面积与这些变量之间的关系建立二次函数的模型;
3.利用二次函数的性质以及自变量的取值范围确定面积的最大值或最小值.
课堂练习
1. 把一根长的铁丝分成两段,每一段弯曲成一个正方形,面积和最小是( )
A. B. C. D.
2.用总长为a米的材料做成如图1所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图2,则a的值是( )
A.16 B.12 C.8 D.4
【答案】B
【分析】因为x=2时,面积最大,为4,根据图形是矩形,由面积公式易得长为2米,从而得出a的值.
【详解】解:由图象可知,当x=2时,y有最大,最大值为4,
∴当x=2米,窗框的最大面积是4平方米,
根据矩形面积计算公式,矩形的长为4÷2=2(米),
∴材料总长a=2×3+2×3=12(米).
故选:B.
3.已知,一个铝合金窗框如图所示,所使用的铝合金材料长度为18cm.设AB长为xm,窗户的总面积为Sm2.
(1)求S关于x的函数表达式.
(2)若AB的长不能低于2m,且AB<BC,求此时窗户总面积S的最大值和最小值.
【答案】(1)S=-+9x
(2)窗户总面积S的最大值m2,最小值是12m2
【分析】(1)根据题意和图形可以求得S与x的函数表达式;
(2)根据题意可以得到关于x的不等式,从而求出x的范围,然后根据(1)中的函数解析式和二次函数的性质即可解答.
3
课堂总结
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
