7.4认识三角形(第1课时)课件(共31张PPT)
文档属性
| 名称 | 7.4认识三角形(第1课时)课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 08:39:06 | ||
图片预览








文档简介
(共31张PPT)
认识三角形(上)
Cognitive triangle
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
认识三角形,掌握三角形及其基本要素的表示方法;
能根据角的度数或边的关系,对三角形进行分类
02
掌握三角形的三边关系,并能根据三边关系解决相关问题
三角形的定义、分类与三边关系
知识精讲
情境引入
01
帆船
知识精讲
情境引入
01
金字塔
知识精讲
情境引入
01
圣诞树
知识精讲
情境引入
01
这些图片里面都有什么形状?
三角形
02
知识精讲
【三角形的定义】
三角形是由3条不在同一条直线上的线段,首尾依次相接组成的图形
三角形的定义
(1)三角形有3条边、3个内角和3个顶点;
(2)顶点是A、B、C的三角形记作“△ABC”;
(3)∠A所对的边BC也可以用a表示,类似地,∠B所对的边AC、∠C所对的边AB也可以分别用b、c表示.
A
B
C
a
b
c
02
知识精讲
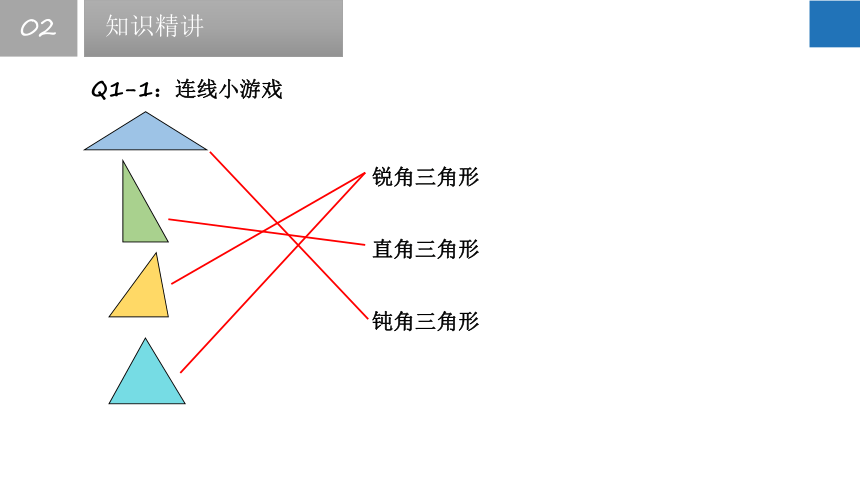
Q1-1:连线小游戏
锐角三角形
直角三角形
钝角三角形
02
知识精讲
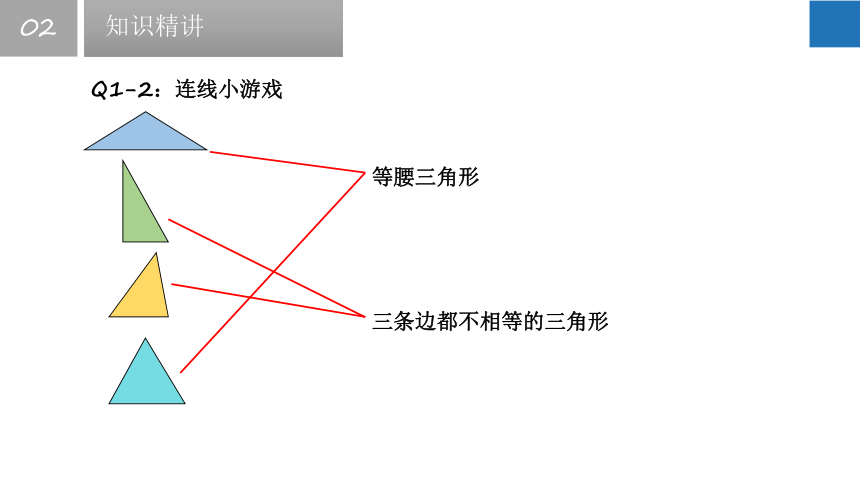
Q1-2:连线小游戏
等腰三角形
三条边都不相等的三角形
02
知识精讲
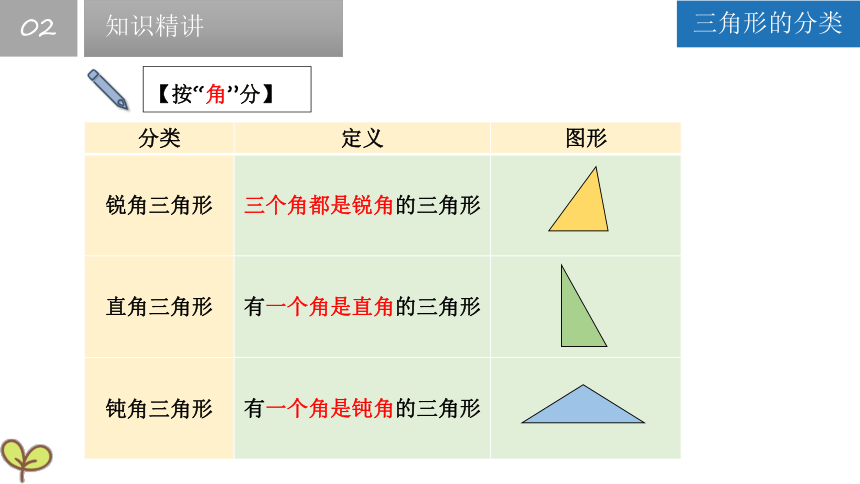
【按“角”分】
三角形的分类
分类 定义 图形
锐角三角形 三个角都是锐角的三角形
直角三角形 有一个角是直角的三角形
钝角三角形 有一个角是钝角的三角形
02
知识精讲
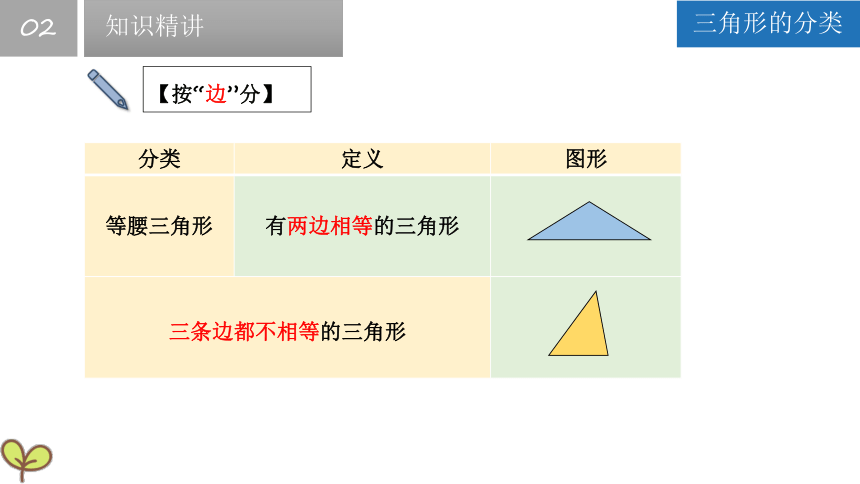
【按“边”分】
三角形的分类
分类 定义 图形
等腰三角形 有两边相等的三角形
三条边都不相等的三角形
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
①3cm、4cm、5cm
3cm
4cm
5cm
可以构成一个三角形,且是直角三角形
3cm
4cm
5cm
8cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
8cm
4cm
3cm
②3cm、4cm、8cm
∵3cm+4cm<8cm
∴无法构成三角形
3cm
4cm
5cm
8cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
8cm
③3cm、5cm、8cm
∵3cm+5cm=8cm
∴无法构成三角形
8cm
5cm
3cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
8cm
④4cm、5cm、8cm
8cm
5cm
4cm
可以构成一个三角形
02
知识精讲
Q2-2:通过上面的操作活动,你发现三角形三边之间有怎样的关系?
分类
①3cm、4cm、5cm 3cm+4cm>5cm 3cm+5cm>4cm 4cm+5cm>3cm √
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
④4cm、5cm、8cm 4cm+5cm>8cm 4cm+8cm>5cm 5cm+8cm>4cm √
三角形的任意两边之和大于第三边
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
分类 两边之和与第三边的关系
02
知识精讲
Q3:如何根据基本事实"两点之间线段最短",说明三角形三边之间的关系?
【分析】
∵BC是连接B、C两点的线段,
根据基本事实"两点之间线段最短"
∴AB+AC>BC
同理,AC+BC>AB,AB+BC>AC
A
B
C
02
知识精讲
Q4:已知三角形的任意两边之和大于第三边,那么两边之差与第三边有何关系?
【分析】
∵AB+AC>BC,AC+BC>AB,AB+BC>AC
∴AB>BC-AC,AC>AB-BC,AB>AC-BC
A
B
C
【结论】
三角形的任意两边之差小于第三边
02
知识精讲
三角形的三边关系
【三角形的三边关系的定理】
三角形的任意两边之和大于第三边
【推论】
三角形的任意两边之差小于第三边
02
知识精讲
三条线段能否围成三角形
【判断三条线段能否围成三角形】
如果任意两条线段的长度之和大于第三条线段的长度,那么这三条线段能围成三角形
02
知识精讲
进一步,只要较短两条线段长度之和大于第三条线段的长度,那么这三条线段能围成三角形
两边之和与第三边的关系
①3cm、4cm、5cm 3cm+4cm>5cm 3cm+5cm>4cm 4cm+5cm>3cm √
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
④4cm、5cm、8cm 4cm+5cm>8cm 4cm+8cm>5cm 5cm+8cm>4cm √
知识精讲
例1、如图,以AB为边的三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
D
【三角形的个数问题】
【分析】
△ABC、△ABE、△ABF、△ABD
知识精讲
例2、如图,共有几个三角形?
【分析】
图(1)中△ABC、△ABD、△ACD——3个
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(2)
(1)
(3)
图(2)中△ABC、△ABE、△ACD、△ABD、△ADE、△ACE——6个
图(3)中△ABC、△ABF、△ACD、△ABE、△ADF、△ACE、△ABD、△ADE、△AEF、△ACF—10个
知识精讲
例2拓展、以此类推,图6共有几个三角形?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(2)6个
(1)3个
(3)10个
【分析】
(1)3=1+2
(2)6=1+2+3
(3)10=1+2+3+4
……
(n)n=1+2+3+……+n=
∴n=6时,共个,即28个三角形
知识精讲
例3、三角形的两边长分别为5和7,第三边长为奇数,这个三角形的周长可以是( )
A.13 B.14 C.15 D.16
C
【三角形的三边关系】
【分析】
设第三边长为x,则7-5<x<7+5,即2<x<12,
∵第三边长为奇数,
∴第三边长为3或5或7或9或11,
∴这个三角形的周长可以是15或17或19或21或23.
知识精讲
例4、用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A.2cm、3cm、3cm B.2cm、2cm、5cm
C.1cm、5cm、3cm D.2cm、5cm、8cm
A
【分析】
A、∵2+3>3,∴能做成三角形框架
B、∵2+2<5,∴不能做成三角形框架
C、∵1+3<5,∴不能做成三角形框架
D、∵2+5<8,∴不能做成三角形框架
解题技巧:
关键看较短两条线段长度之和大于第三条线段的长度
知识精讲
例5、木工王师傅用四根木条做了一个四边形框架.要使这个框架不变形,他至少需要再钉上木条的数量是( )
A.0条 B.1条 C.2条 D.3条
B
【三角形的稳定性】
【分析】
如图所示:
要使这个木架不变形,他至少还要再钉上1个木条.
牢记:
三角形具有稳定性
知识精讲
例6、下列生活实物中,没有用到三角形的稳定性的是( )
A. B.
C. D.
B
课后总结
【三角形的分类】
按“角”分:锐角三角形、直角三角形、钝角三角形
按“边”分:等腰三角形、三条边都不相等的三角形
【三角形的定义】
三角形是由3条不在同一条直线上的线段,首尾依次相接组成的图形
【三角形的三边关系的定理及推论】
定理:三角形的任意两边之和大于第三边
推论:三角形的任意两边之差小于第三边
【判断三条线段能否围成三角形】
如果任意两条线段的长度之和大于第三条线段的长度,那么这三条线段能围成三角形
精简版——如果较短两条线段长度之和大于第三条线段的长度,那么这三条线段能围成三角形
谢谢学习
Thank you for learning
认识三角形(上)
Cognitive triangle
苏科版七年级下册第7章平面图形的认识(二)
教学目标
01
认识三角形,掌握三角形及其基本要素的表示方法;
能根据角的度数或边的关系,对三角形进行分类
02
掌握三角形的三边关系,并能根据三边关系解决相关问题
三角形的定义、分类与三边关系
知识精讲
情境引入
01
帆船
知识精讲
情境引入
01
金字塔
知识精讲
情境引入
01
圣诞树
知识精讲
情境引入
01
这些图片里面都有什么形状?
三角形
02
知识精讲
【三角形的定义】
三角形是由3条不在同一条直线上的线段,首尾依次相接组成的图形
三角形的定义
(1)三角形有3条边、3个内角和3个顶点;
(2)顶点是A、B、C的三角形记作“△ABC”;
(3)∠A所对的边BC也可以用a表示,类似地,∠B所对的边AC、∠C所对的边AB也可以分别用b、c表示.
A
B
C
a
b
c
02
知识精讲
Q1-1:连线小游戏
锐角三角形
直角三角形
钝角三角形
02
知识精讲
Q1-2:连线小游戏
等腰三角形
三条边都不相等的三角形
02
知识精讲
【按“角”分】
三角形的分类
分类 定义 图形
锐角三角形 三个角都是锐角的三角形
直角三角形 有一个角是直角的三角形
钝角三角形 有一个角是钝角的三角形
02
知识精讲
【按“边”分】
三角形的分类
分类 定义 图形
等腰三角形 有两边相等的三角形
三条边都不相等的三角形
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
①3cm、4cm、5cm
3cm
4cm
5cm
可以构成一个三角形,且是直角三角形
3cm
4cm
5cm
8cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
8cm
4cm
3cm
②3cm、4cm、8cm
∵3cm+4cm<8cm
∴无法构成三角形
3cm
4cm
5cm
8cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
8cm
③3cm、5cm、8cm
∵3cm+5cm=8cm
∴无法构成三角形
8cm
5cm
3cm
02
知识精讲
Q2-1:从长度分别为3cm、4cm、5cm、8cm的小木棒(如图)中任意取3根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
8cm
④4cm、5cm、8cm
8cm
5cm
4cm
可以构成一个三角形
02
知识精讲
Q2-2:通过上面的操作活动,你发现三角形三边之间有怎样的关系?
分类
①3cm、4cm、5cm 3cm+4cm>5cm 3cm+5cm>4cm 4cm+5cm>3cm √
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
④4cm、5cm、8cm 4cm+5cm>8cm 4cm+8cm>5cm 5cm+8cm>4cm √
三角形的任意两边之和大于第三边
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
分类 两边之和与第三边的关系
02
知识精讲
Q3:如何根据基本事实"两点之间线段最短",说明三角形三边之间的关系?
【分析】
∵BC是连接B、C两点的线段,
根据基本事实"两点之间线段最短"
∴AB+AC>BC
同理,AC+BC>AB,AB+BC>AC
A
B
C
02
知识精讲
Q4:已知三角形的任意两边之和大于第三边,那么两边之差与第三边有何关系?
【分析】
∵AB+AC>BC,AC+BC>AB,AB+BC>AC
∴AB>BC-AC,AC>AB-BC,AB>AC-BC
A
B
C
【结论】
三角形的任意两边之差小于第三边
02
知识精讲
三角形的三边关系
【三角形的三边关系的定理】
三角形的任意两边之和大于第三边
【推论】
三角形的任意两边之差小于第三边
02
知识精讲
三条线段能否围成三角形
【判断三条线段能否围成三角形】
如果任意两条线段的长度之和大于第三条线段的长度,那么这三条线段能围成三角形
02
知识精讲
进一步,只要较短两条线段长度之和大于第三条线段的长度,那么这三条线段能围成三角形
两边之和与第三边的关系
①3cm、4cm、5cm 3cm+4cm>5cm 3cm+5cm>4cm 4cm+5cm>3cm √
②3cm、4cm、8cm 3cm+4cm<8cm 3cm+8cm>4cm 4cm+8cm>3cm ×
③3cm、5cm、8cm 3cm+5cm=8cm 3cm+8cm>5cm 5cm+8cm>3cm ×
④4cm、5cm、8cm 4cm+5cm>8cm 4cm+8cm>5cm 5cm+8cm>4cm √
知识精讲
例1、如图,以AB为边的三角形的个数是( )
A.1个 B.2个 C.3个 D.4个
D
【三角形的个数问题】
【分析】
△ABC、△ABE、△ABF、△ABD
知识精讲
例2、如图,共有几个三角形?
【分析】
图(1)中△ABC、△ABD、△ACD——3个
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(2)
(1)
(3)
图(2)中△ABC、△ABE、△ACD、△ABD、△ADE、△ACE——6个
图(3)中△ABC、△ABF、△ACD、△ABE、△ADF、△ACE、△ABD、△ADE、△AEF、△ACF—10个
知识精讲
例2拓展、以此类推,图6共有几个三角形?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
(2)6个
(1)3个
(3)10个
【分析】
(1)3=1+2
(2)6=1+2+3
(3)10=1+2+3+4
……
(n)n=1+2+3+……+n=
∴n=6时,共个,即28个三角形
知识精讲
例3、三角形的两边长分别为5和7,第三边长为奇数,这个三角形的周长可以是( )
A.13 B.14 C.15 D.16
C
【三角形的三边关系】
【分析】
设第三边长为x,则7-5<x<7+5,即2<x<12,
∵第三边长为奇数,
∴第三边长为3或5或7或9或11,
∴这个三角形的周长可以是15或17或19或21或23.
知识精讲
例4、用下列长度的三根木棒首尾相接,能做成三角形框架的是( )
A.2cm、3cm、3cm B.2cm、2cm、5cm
C.1cm、5cm、3cm D.2cm、5cm、8cm
A
【分析】
A、∵2+3>3,∴能做成三角形框架
B、∵2+2<5,∴不能做成三角形框架
C、∵1+3<5,∴不能做成三角形框架
D、∵2+5<8,∴不能做成三角形框架
解题技巧:
关键看较短两条线段长度之和大于第三条线段的长度
知识精讲
例5、木工王师傅用四根木条做了一个四边形框架.要使这个框架不变形,他至少需要再钉上木条的数量是( )
A.0条 B.1条 C.2条 D.3条
B
【三角形的稳定性】
【分析】
如图所示:
要使这个木架不变形,他至少还要再钉上1个木条.
牢记:
三角形具有稳定性
知识精讲
例6、下列生活实物中,没有用到三角形的稳定性的是( )
A. B.
C. D.
B
课后总结
【三角形的分类】
按“角”分:锐角三角形、直角三角形、钝角三角形
按“边”分:等腰三角形、三条边都不相等的三角形
【三角形的定义】
三角形是由3条不在同一条直线上的线段,首尾依次相接组成的图形
【三角形的三边关系的定理及推论】
定理:三角形的任意两边之和大于第三边
推论:三角形的任意两边之差小于第三边
【判断三条线段能否围成三角形】
如果任意两条线段的长度之和大于第三条线段的长度,那么这三条线段能围成三角形
精简版——如果较短两条线段长度之和大于第三条线段的长度,那么这三条线段能围成三角形
谢谢学习
Thank you for learning
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
