17.1 勾股定理(第1课时)课件(共37张PPT)
文档属性
| 名称 | 17.1 勾股定理(第1课时)课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 08:36:35 | ||
图片预览





文档简介
(共37张PPT)
17.1勾股定理(第1课时)
第17章 勾股定理
教师
xxx
人教版 八年级下册
勾股定理
美丽的勾股树
勾股定理的证明
拓展视野:勾股定理的其他证法
01
03
02
04
CONTANTS
目 录
勾股定理
01
相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系.
观察一下,你能从中发现什么数量关系吗
情景引入
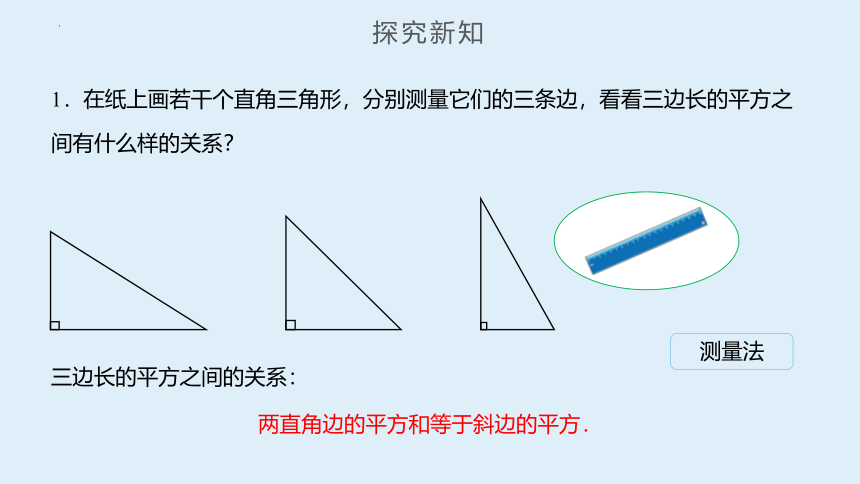
1.在纸上画若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?
两直角边的平方和等于斜边的平方.
三边长的平方之间的关系:
测量法
探究新知
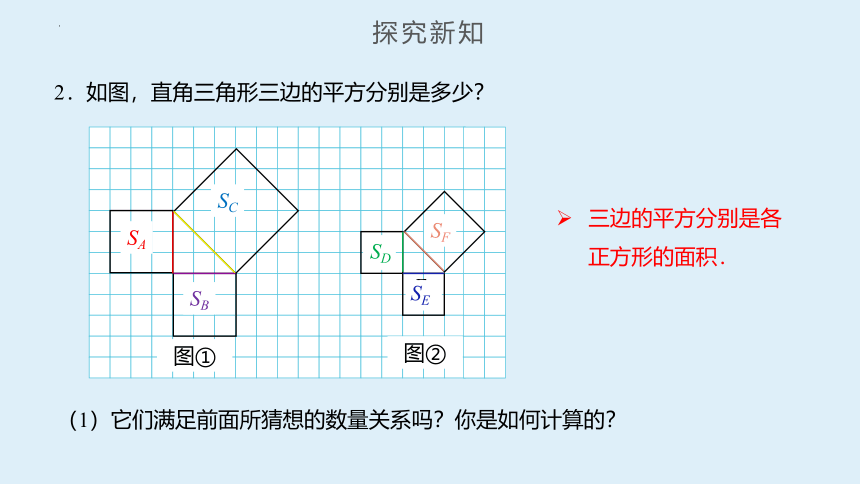
2.如图,直角三角形三边的平方分别是多少?
A
C
B
D
F
E
图①
图②
三边的平方分别是各正方形的面积.
SA
SB
SC
SF
SD
SE
(1)它们满足前面所猜想的数量关系吗?你是如何计算的?
探究新知
A
C
B
图①
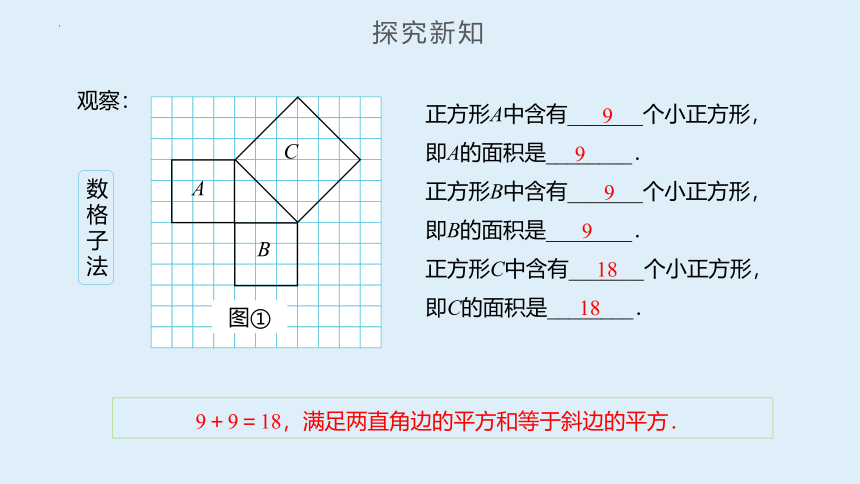
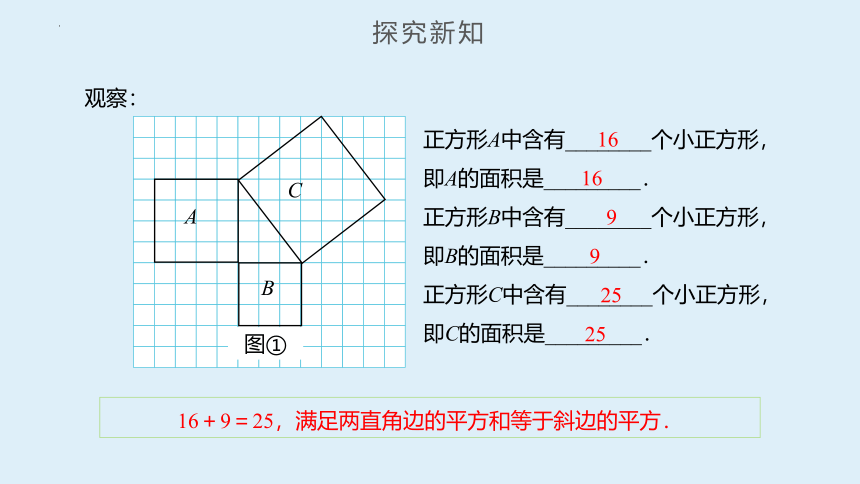
正方形A中含有_______个小正方形,
即A的面积是________.
正方形B中含有_______个小正方形,
即B的面积是________.
正方形C中含有_______个小正方形,
即C的面积是________.
观察:
9
9
9
9
18
18
9+9=18,满足两直角边的平方和等于斜边的平方.
数格子法
探究新知
D
F
E
图②
正方形D中含有_______个小正方形,
即D的面积是________.
正方形E中含有_______个小正方形,
即E的面积是________.
正方形F中含有_______个小正方形,
即F的面积是________.
4
4
4
4
8
8
4+4=8,满足两直角边的平方和等于斜边的平方.
观察:
探究新知
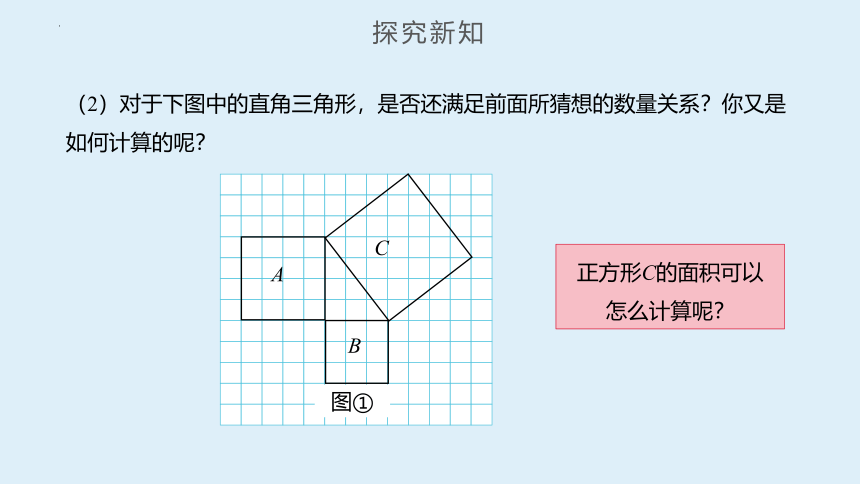
(2)对于下图中的直角三角形,是否还满足前面所猜想的数量关系?你又是如何计算的呢?
A
C
B
图①
正方形C的面积可以
怎么计算呢?
探究新知
A
C
B
图①
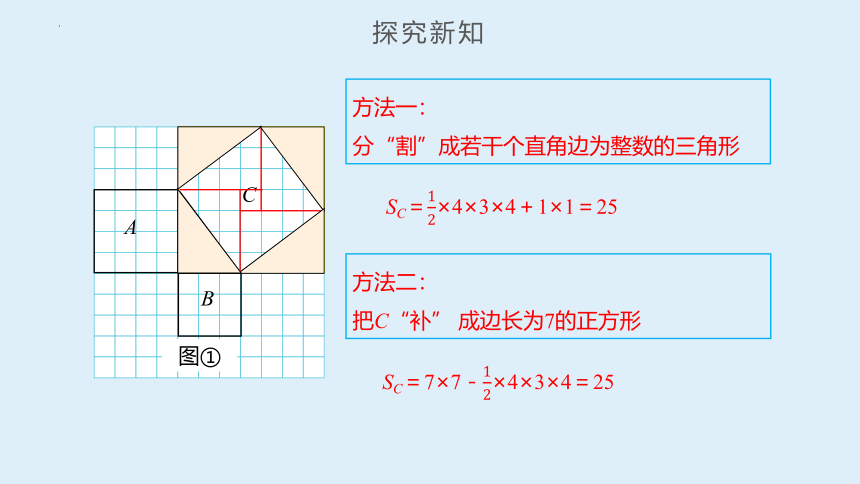
方法一:
分“割”成若干个直角边为整数的三角形
SC=×4×3×4+1×1=25
方法二:
把C“补” 成边长为7的正方形
SC=7×7-×4×3×4=25
探究新知
正方形A中含有________个小正方形,
即A的面积是_________.
正方形B中含有________个小正方形,
即B的面积是_________.
正方形C中含有________个小正方形,
即C的面积是_________.
16
16
9
9
25
25
16+9=25,满足两直角边的平方和等于斜边的平方.
观察:
A
C
B
图①
探究新知
勾股定理
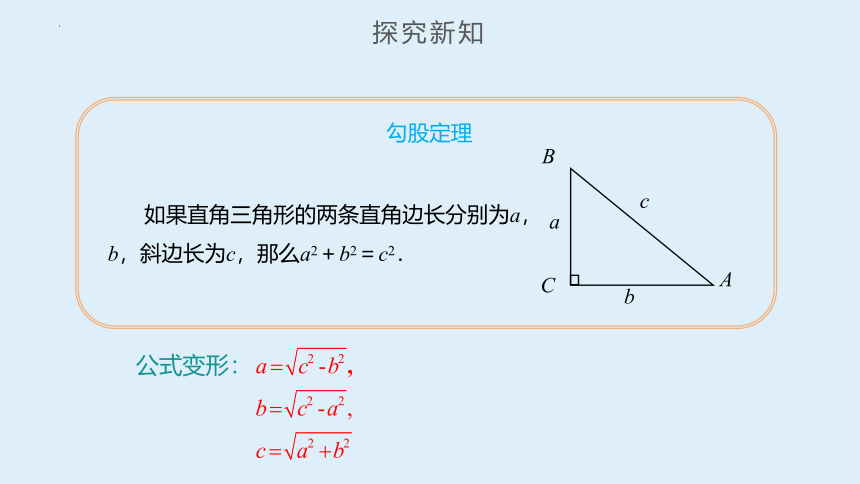
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
B
C
a
b
c
探究新知
公式变形:
勾
股
弦
我国古代把直角三角形中
较短的直角边称为勾,
较长的直角边称为股,
斜边称为弦,
“勾股定理”因此而得名.
(在很多国家文献中称为毕达哥拉斯定理)
探究新知
解:(1)∵a2+b2=c2,即 32+b2=52,
又 b>0,∴ b=4.
例题1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=3,c=5,求 b;
(2)已知 a=10,b=24,求 c;
(3)已知 c=17,b=8,求 a.
(2)∵ a2+b2=c2,即 102+242=c2,
又 c>0,∴c=26.
(3)∵ a2+b2=c2,即 a2+82=172,
又 a>0,∴ a=15.
首先分清斜边和直角边,然后利用“直角三角形两直角边的平方和等于斜边的平方”即可求出未知边的长.
典型例题
勾股定理的证明
02
“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,右图是弦图的示意图.
c
b
a
黄实
朱实
弦图由四个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,尝试验证:
a2+b2=c2.
弦图
探究新知
赵爽证法
尝试验证:a2+b2=c2.
化简得:c2 =a2+b2.
S大正方形 =S小正方形+4S直角三角形
c2 =(b-a)2+4·.
这就证明了勾股定理.
证明:
c
b
a
黄实
朱实
弦图
探究新知
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,尝试证明勾股定理.
化简得:c2 =a2+b2.
S大正方形=S小正方形+4S直角三角形
(b+a)2 = c2+4·.
证明:
c
b
a
a
b
a
a
b
c
c
c
b
探究新知
毕达哥拉斯证法
a
a
b
b
c
c
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
探究新知
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
例题2 在Rt△ABC中,∠C=90°.
解:
(1)设a=x,b=2x,由勾股定理得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理得
(2x)2-x2=152,
解得
C
A
B
a
b
c
典型例题
1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
针对练习
美丽的勾股树
03
1
1
美丽的勾股树
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
探究新知
例题3 求下列图中表示边长的未知数x、y、z的值.
(1) (2) (3)
36
64
x
y
z
625
576
144
169
解:(1) x 10; (2) y 5 ; (3) z 7.
典型例题
结论:
S1+S2+S3+S4
=S5+S6
=S7
例题4 已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值.
典型例题
勾股定理的历史
勾股定理有着悠久的历史:古巴比伦人和古代中国人看出了这个关系(即直角三角形三边关系),古希腊的毕达哥拉斯学派首先证明了这个关系。
勾股定理也有很多别称,也叫毕达哥拉斯定理、百牛定理、商高定理、驴桥定理和埃及三角形等。
勾股定理被誉为“人类最伟大的十个科学发现之一”,是初等几何中的一个基本定理。在我们今后的几何计算题和推理题中都有着广泛的应用。
迄今为止,勾股定理大约有500多种证明方法,是证明方法最多的
定理之一。
探究新知
拓展视野:勾股定理的其他证法
04
达·芬奇对勾股定理的证明
探究新知
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
探究新知
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
探究新知
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
课堂练习
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
17
5
74或24
课堂练习
5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 =172,
即x2=172-152=289–225=64,
∴ x=±8(负值舍去),
∴另一直角边长为8 cm,
直角三角形的面积是
(cm2).
课堂练习
6.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB= .
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD= ,∴BC=BD+CD=1+ ,
∴△ABC的周长=AB+AC+BC= .
课堂练习
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
课堂练习
注意
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c .
1.勾股定理的适用条件:在直角三角形中;
2.熟悉常见的公式变形;
3.当不能确定哪条边是斜边时,需分类讨论.
a
b
c
勾股定理
课堂小结
感谢观看
17.1勾股定理(第1课时)
第17章 勾股定理
教师
xxx
人教版 八年级下册
勾股定理
美丽的勾股树
勾股定理的证明
拓展视野:勾股定理的其他证法
01
03
02
04
CONTANTS
目 录
勾股定理
01
相传在2500多年以前,毕达哥拉斯在朋友家做客时,发现朋友家用地砖铺成的地面图案反映了直角三角形的某种数量关系.
观察一下,你能从中发现什么数量关系吗
情景引入
1.在纸上画若干个直角三角形,分别测量它们的三条边,看看三边长的平方之间有什么样的关系?
两直角边的平方和等于斜边的平方.
三边长的平方之间的关系:
测量法
探究新知
2.如图,直角三角形三边的平方分别是多少?
A
C
B
D
F
E
图①
图②
三边的平方分别是各正方形的面积.
SA
SB
SC
SF
SD
SE
(1)它们满足前面所猜想的数量关系吗?你是如何计算的?
探究新知
A
C
B
图①
正方形A中含有_______个小正方形,
即A的面积是________.
正方形B中含有_______个小正方形,
即B的面积是________.
正方形C中含有_______个小正方形,
即C的面积是________.
观察:
9
9
9
9
18
18
9+9=18,满足两直角边的平方和等于斜边的平方.
数格子法
探究新知
D
F
E
图②
正方形D中含有_______个小正方形,
即D的面积是________.
正方形E中含有_______个小正方形,
即E的面积是________.
正方形F中含有_______个小正方形,
即F的面积是________.
4
4
4
4
8
8
4+4=8,满足两直角边的平方和等于斜边的平方.
观察:
探究新知
(2)对于下图中的直角三角形,是否还满足前面所猜想的数量关系?你又是如何计算的呢?
A
C
B
图①
正方形C的面积可以
怎么计算呢?
探究新知
A
C
B
图①
方法一:
分“割”成若干个直角边为整数的三角形
SC=×4×3×4+1×1=25
方法二:
把C“补” 成边长为7的正方形
SC=7×7-×4×3×4=25
探究新知
正方形A中含有________个小正方形,
即A的面积是_________.
正方形B中含有________个小正方形,
即B的面积是_________.
正方形C中含有________个小正方形,
即C的面积是_________.
16
16
9
9
25
25
16+9=25,满足两直角边的平方和等于斜边的平方.
观察:
A
C
B
图①
探究新知
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
B
C
a
b
c
探究新知
公式变形:
勾
股
弦
我国古代把直角三角形中
较短的直角边称为勾,
较长的直角边称为股,
斜边称为弦,
“勾股定理”因此而得名.
(在很多国家文献中称为毕达哥拉斯定理)
探究新知
解:(1)∵a2+b2=c2,即 32+b2=52,
又 b>0,∴ b=4.
例题1 设直角三角形的两条直角边长分别为 a 和 b,斜边长为 c.
(1)已知 a=3,c=5,求 b;
(2)已知 a=10,b=24,求 c;
(3)已知 c=17,b=8,求 a.
(2)∵ a2+b2=c2,即 102+242=c2,
又 c>0,∴c=26.
(3)∵ a2+b2=c2,即 a2+82=172,
又 a>0,∴ a=15.
首先分清斜边和直角边,然后利用“直角三角形两直角边的平方和等于斜边的平方”即可求出未知边的长.
典型例题
勾股定理的证明
02
“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,右图是弦图的示意图.
c
b
a
黄实
朱实
弦图由四个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,尝试验证:
a2+b2=c2.
弦图
探究新知
赵爽证法
尝试验证:a2+b2=c2.
化简得:c2 =a2+b2.
S大正方形 =S小正方形+4S直角三角形
c2 =(b-a)2+4·.
这就证明了勾股定理.
证明:
c
b
a
黄实
朱实
弦图
探究新知
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,尝试证明勾股定理.
化简得:c2 =a2+b2.
S大正方形=S小正方形+4S直角三角形
(b+a)2 = c2+4·.
证明:
c
b
a
a
b
a
a
b
c
c
c
b
探究新知
毕达哥拉斯证法
a
a
b
b
c
c
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
探究新知
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
例题2 在Rt△ABC中,∠C=90°.
解:
(1)设a=x,b=2x,由勾股定理得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理得
(2x)2-x2=152,
解得
C
A
B
a
b
c
典型例题
1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
针对练习
美丽的勾股树
03
1
1
美丽的勾股树
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
探究新知
例题3 求下列图中表示边长的未知数x、y、z的值.
(1) (2) (3)
36
64
x
y
z
625
576
144
169
解:(1) x 10; (2) y 5 ; (3) z 7.
典型例题
结论:
S1+S2+S3+S4
=S5+S6
=S7
例题4 已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值.
典型例题
勾股定理的历史
勾股定理有着悠久的历史:古巴比伦人和古代中国人看出了这个关系(即直角三角形三边关系),古希腊的毕达哥拉斯学派首先证明了这个关系。
勾股定理也有很多别称,也叫毕达哥拉斯定理、百牛定理、商高定理、驴桥定理和埃及三角形等。
勾股定理被誉为“人类最伟大的十个科学发现之一”,是初等几何中的一个基本定理。在我们今后的几何计算题和推理题中都有着广泛的应用。
迄今为止,勾股定理大约有500多种证明方法,是证明方法最多的
定理之一。
探究新知
拓展视野:勾股定理的其他证法
04
达·芬奇对勾股定理的证明
探究新知
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
探究新知
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
探究新知
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
课堂练习
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是5和7,则第三边长的平方为_________.
17
5
74或24
课堂练习
5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得152+ x2 =172,
即x2=172-152=289–225=64,
∴ x=±8(负值舍去),
∴另一直角边长为8 cm,
直角三角形的面积是
(cm2).
课堂练习
6.如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1,求△ABC的周长.
解:∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ADB中,∵∠B+∠BAD=90°,∠B=45°,
∴∠B=∠BAD=45°,
∴BD=AD=1,∴AB= .
在Rt△ADC中,∵∠C=30°,
∴AC=2AD=2,
∴CD= ,∴BC=BD+CD=1+ ,
∴△ABC的周长=AB+AC+BC= .
课堂练习
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
课堂练习
注意
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a b c .
1.勾股定理的适用条件:在直角三角形中;
2.熟悉常见的公式变形;
3.当不能确定哪条边是斜边时,需分类讨论.
a
b
c
勾股定理
课堂小结
感谢观看
