第二单元圆锥与圆锥解决问题 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第二单元圆锥与圆锥解决问题 小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1022.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 18:39:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二单元圆锥和圆锥解决问题-小学数学六年级下册苏教版
1.一台压路机的前轮是一个圆柱形铁轮,轮宽1.5米,直径1米.
(1)前轮每分钟转动4周,每分钟压路的面积是多少平方米?
(2)每立方米铁约重8吨,这个前轮一共重多少吨?
2.圆柱体容器A和B的深度相等,底面半径分别为3厘米和4厘米,把A容器装满水倒入B容器里,水深比容器的低1.2 厘米.B容器的深度是多少厘米?
3.如图,长方形纸片ABCD中,AB=3厘米,BC=4厘米,如果以BC为底边,把纸片卷成一个圆柱,其体积为V1;如果以AB为底边,把纸片卷成一个圆柱,其体积为V2,求V1:V2.
4.把一个底面半径为15厘米的圆锥形零件完全浸没在一个底面半径为30厘米圆柱形储水箱里,当把零件从水箱中取出后,水箱里的水面下降了2.5厘米,这个圆锥形零件的高是多少?
5.一个钢质的圆柱体零件重1763.424克,它的侧面展开图是一个长方形,长方形的长(不是圆柱体的高)是18.84厘米,求这个圆柱体的高(每立方厘米钢重7.8克).
6.从一根截面直径是6分米的圆柱形钢材上截下2米,每立方分米钢重7.8千克,截下的这段钢重多少千克?
7.一个圆锥形的沙堆,底面周长是18.84米,高是1.2米.
(1)这个沙堆的占地面积是多少平方米?
(2)如果将这堆沙装在一个底面积是3.6平方米的圆柱形的坑里,能装多高?
8.一个圆柱形的水桶,底面直径和高都是6分米,如果每升水重1千克,这个水桶能装水多少千克?
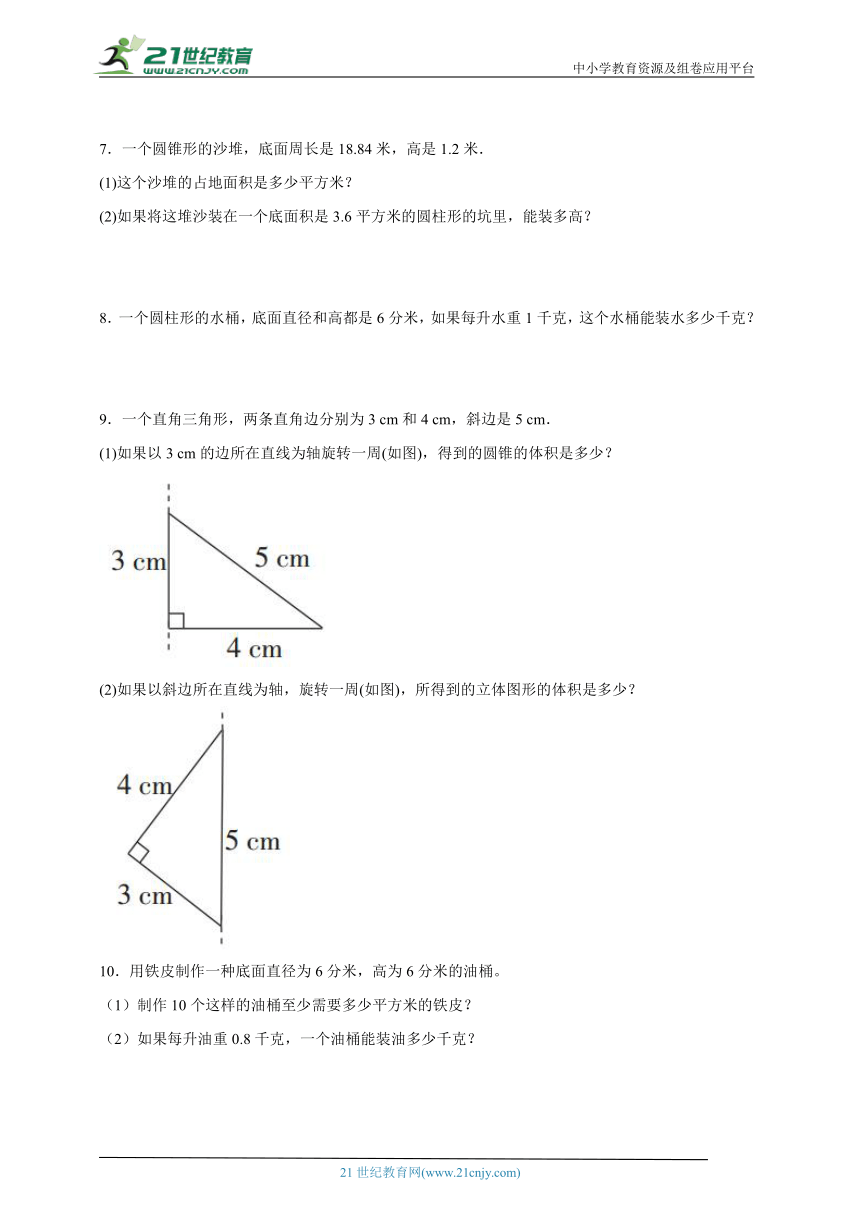
9.一个直角三角形,两条直角边分别为3 cm和4 cm,斜边是5 cm.
(1)如果以3 cm的边所在直线为轴旋转一周(如图),得到的圆锥的体积是多少?
(2)如果以斜边所在直线为轴,旋转一周(如图),所得到的立体图形的体积是多少?
10.用铁皮制作一种底面直径为6分米,高为6分米的油桶。
(1)制作10个这样的油桶至少需要多少平方米的铁皮?
(2)如果每升油重0.8千克,一个油桶能装油多少千克?
11.一个圆柱形蓄水池,底面直径6米,深5米,在水池里面抹一层水泥,抹水泥面的面积是多少平方米?
12.有一个粮囤,上面是圆锥形,下面是圆柱形,底面直径是2米,圆柱高1.8米,圆锥高是0.6米,如果每立方米粮食重700千克,这个粮囤装粮多少千克?
13.一根圆形钢管,内直径4厘米,壁厚2厘米,长2米,这根钢管重多少千克?(钢每立方分米重7.8千克)
14.把一个圆锥形的零件浸没在一个底面半径4分米的盛水的圆柱形杯子中,水面上升3分米.这个圆锥的体积是多少立方分米?
15.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个直径6米的半圆形.
(1)搭建这个大棚大约要用多少平方米的塑料薄膜?
(2)大棚内的空间大约有多少立方米?
16.一个圆柱形水杯,底面直径10厘米,高40厘米,现在有10升的水倒入这个水杯中,可以倒满几杯?
17.一个圆柱形容器的底面半径是4分米,高是6分米,里面盛满水,倒进棱长是8分米的正方体容器内,水深是多少分米?
18.一卷透明胶带,它的外直径是5厘米,内直径是4厘米,胶带宽2厘米.这卷透明胶带的外大圆柱体积是多少立方厘米?内小圆柱体积是多少立方厘米?
参考答案:
1.每分钟压路的面积是18.84平方米,这个前轮一共重多9.42吨.
【详解】试题分析:(1)所压的路面是一个长方形平面,它的长就是压路机前进的米数,宽1.5米(已知),根据长方形面积计算公式,即可求出所压的面积.
(2)首先根据圆柱的体积公式:v=sh,求出压路机前轮的体积,再乘每立方米铁的质量即可.
解:(1)3.14×1×4×1.5,
=12.56×1.5,
=18.84(平方米);
(2)3.14×()2×1.5×8,
=3.14×0.25×1.5×8,
=1.1775×8,
=9.42(吨);
答:每分钟压路的面积是18.84平方米,这个前轮一共重多9.42吨.
点评:此题主要考查圆的周长公式、圆柱的体积公式的实际应用.
2.6.4厘米
【详解】试题分析:根据题意可知,容器A和B底面半径的比是3:4,那么两圆柱体容器的底面积比是9:16;又知道容器A和B的深度相等,高相等,所以容器A的体积是容器B体积的;由此列式解答.
解:(3.14×32)÷(3.14×42)
=(3.14×9)÷(3.14×16)
=28.26÷50.24
=;
1.2÷(﹣)
=1.2÷
=1.2×
=6.4(厘米);
答:B容器的深度是6.4厘米.
点评:此题解答的关键根据两个圆柱体的高相等,它们底面积的比等于底面半径的平方比,就是求出两个容器体积的比,;再根据已知比一个数少几分之几的数是多少,求这个数,用除法解答.
3.4:3
【详解】试题分析:如果以BC为底边,把纸片卷成一个圆柱,则圆柱的底面周长为4厘米,高为3厘米,体积为:V1=π×3;如果以AB为底边,把纸片卷成一个圆柱,则圆柱的底面周长为3厘米,高为4厘米,体积为:V2=π×4;由此写出V1与V2的比,化简比即可得出答案.
解:V1:V2=[π×3]:[π×4];
=[16×3]:[9×4];
=4:3;
答:V1:V2=4:3.
点评:此题主要考查圆柱的体积公式及化简比,关键要知道两次把长方形纸卷成圆柱的底面周长和高,代入公式表示出两个圆柱体积,化简比即可.
4.3厘米.
【详解】试题分析:由题意知,水面下降2.5厘米的水的体积就是这个圆锥形零件的体积,由此利用圆柱的体积=πr2h,计算出这个圆锥形零件的体积;再利用圆锥的高=圆锥的体积×3÷底面积进行解答.
解:下降2.5厘米的水的体积即这个圆锥形零件的体积为:
3.14×302×2.5,
=3.14×900×2.5,
=282.6×2.5,
=706.5(立方厘米);
所以圆锥形零件的高为:
706.5×3÷(3.14×152),
=2119.5÷706.5,
=3(厘米);
答:这个圆锥形零件的高是3厘米.
点评:此题考查了圆柱与圆锥的体积公式的灵活应用,这里根据下降的水的体积求得圆锥形零件的体积是本题的关键.再根据体积公式列式解答且不要漏了.
5.8厘米
【详解】试题分析:先求出圆柱体零件的体积,再求出圆柱体的底面半径,那底面积即可求出,最后即可求出圆柱体的高.
解:圆柱体的体积:1763.424÷7.8=226.08(立方厘米),
底面半径是:18.84÷3.14÷2=3(厘米),
底面积是:3.14×32=3.14×9=28.26(平方厘米),
高是:226.08÷28.26=8(厘米),
答:这个圆柱体的高是8厘米.
点评:此题主要考查了圆柱体的体积公式的灵活应用.
6.2米=20分米 6÷2=3(分米)
3×3×3.14×20×7.8=4408.56(千克)
【详解】略
7.(1)18.84÷3.14÷2=3(米)
3.14×32=28.26(平方米)
答:这个沙堆的占地面积是28.26平方米.
(2)28.26×1.2×÷3.6=3.14(米)
答:能装3.14米高.
【详解】略
8.3.14×(6÷2)2×6×1=169.56(立方分米)
169.56立方分米=169.56升
答:这个水桶能装水169.56千克.
【详解】略
9.(1)×3.14×42×3=50.24(cm3)
答:得到的圆锥的体积是50.24 cm3.
(2)3×4÷5=2.4(cm)
×3.14×2.42×5=30.144(cm3)
答:所得到的立体图形的体积是30.144 cm3.
【详解】略
10.(1)16.956平方米
(2)135.648千克
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,求出一个圆柱的表面积乘10即可。
(2)求出油桶的容积的升数乘0.8即可。
【详解】(1)6÷2=3(分米)
(6×3.14×6+3×3×3.14×2)×10
=(113.04+56.52)×10
=169.56×10
=1695.6(平方分米)
=16.956平方米
答:制作10个这样的油桶至少需要16.956平方米的铁皮。
(2)3×3×3.14×6×0.8
=28.26×6×0.8
=169.56×0.8
=135.648(千克)
答:一个油桶能装油135.648千克。
【点睛】此题考查圆柱的表面积、体积相关应用。掌握其公式是解题关键。
11.122.46平方米
【详解】3.14× +3.14×6×5=122.46(平方米)
答:抹水泥面的面积是122.46平方米.
12.4396千克
【详解】粮囤的底面积:3.14×( )2=3.14(平方米)
粮囤的体积:3.14×18+3.14×0.6× =6.28(立方米)
粮食重量:700×6.28=4396(千克)
答:这个粮囤装粮4396千克.
13.58.7808千克
【详解】4厘米=0.4分米,2厘米=0.2分米,2米=20分米
内半径:0.4÷2=0.2(分米)
外半径:0.2+0.2=0.4(分米)
钢管体积:3.14×(0.42-0.22)×20=7.536(立方分米)
钢管重量:7.8×7.536=58.7808(千克)
答:这根钢管重58.7808千克.
14.48π
【详解】略
15.(1)69π (2)90π
【详解】略
16.3杯
【详解】3.14×(10÷2) ×40
=3.14×1000
=3140(立方厘米)
3140立方厘米=3.14升
10÷3.14≈3(杯〕
答:可以倒满3杯。
17.4.71分米
【分析】根据圆柱体积=底面积×高,求出圆柱容积,用圆柱容积÷正方体容器底面积即可。
【详解】3.14×4 ×6
=50.24×6
=301.44(立方分米)
301.44÷(8×8)
=301.44÷64
=4.71(分米)
答:水深是4.71分米。
【点睛】关键是掌握圆柱和长方体体积公式。
18.V外:39.25立方厘米 V内:25.12立方厘米
【分析】根据题意可知,利用圆柱体积公式:,代数解答即可。
【详解】3.14×(5÷2)×2
=3.14×6.25×2
=19.625×2
=39.25(立方厘米)
答:这卷透明胶带的外大圆柱体积是39.25立方厘米。
3.14×(4÷2)×2
=3.14×4×2
=25.12(立方厘米)
答:这卷透明胶带的内小圆柱体积是25.12立方厘米。
【点睛】此题主要考查学生对圆柱体积公式的实际应用解题能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元圆锥和圆锥解决问题-小学数学六年级下册苏教版
1.一台压路机的前轮是一个圆柱形铁轮,轮宽1.5米,直径1米.
(1)前轮每分钟转动4周,每分钟压路的面积是多少平方米?
(2)每立方米铁约重8吨,这个前轮一共重多少吨?
2.圆柱体容器A和B的深度相等,底面半径分别为3厘米和4厘米,把A容器装满水倒入B容器里,水深比容器的低1.2 厘米.B容器的深度是多少厘米?
3.如图,长方形纸片ABCD中,AB=3厘米,BC=4厘米,如果以BC为底边,把纸片卷成一个圆柱,其体积为V1;如果以AB为底边,把纸片卷成一个圆柱,其体积为V2,求V1:V2.
4.把一个底面半径为15厘米的圆锥形零件完全浸没在一个底面半径为30厘米圆柱形储水箱里,当把零件从水箱中取出后,水箱里的水面下降了2.5厘米,这个圆锥形零件的高是多少?
5.一个钢质的圆柱体零件重1763.424克,它的侧面展开图是一个长方形,长方形的长(不是圆柱体的高)是18.84厘米,求这个圆柱体的高(每立方厘米钢重7.8克).
6.从一根截面直径是6分米的圆柱形钢材上截下2米,每立方分米钢重7.8千克,截下的这段钢重多少千克?
7.一个圆锥形的沙堆,底面周长是18.84米,高是1.2米.
(1)这个沙堆的占地面积是多少平方米?
(2)如果将这堆沙装在一个底面积是3.6平方米的圆柱形的坑里,能装多高?
8.一个圆柱形的水桶,底面直径和高都是6分米,如果每升水重1千克,这个水桶能装水多少千克?
9.一个直角三角形,两条直角边分别为3 cm和4 cm,斜边是5 cm.
(1)如果以3 cm的边所在直线为轴旋转一周(如图),得到的圆锥的体积是多少?
(2)如果以斜边所在直线为轴,旋转一周(如图),所得到的立体图形的体积是多少?
10.用铁皮制作一种底面直径为6分米,高为6分米的油桶。
(1)制作10个这样的油桶至少需要多少平方米的铁皮?
(2)如果每升油重0.8千克,一个油桶能装油多少千克?
11.一个圆柱形蓄水池,底面直径6米,深5米,在水池里面抹一层水泥,抹水泥面的面积是多少平方米?
12.有一个粮囤,上面是圆锥形,下面是圆柱形,底面直径是2米,圆柱高1.8米,圆锥高是0.6米,如果每立方米粮食重700千克,这个粮囤装粮多少千克?
13.一根圆形钢管,内直径4厘米,壁厚2厘米,长2米,这根钢管重多少千克?(钢每立方分米重7.8千克)
14.把一个圆锥形的零件浸没在一个底面半径4分米的盛水的圆柱形杯子中,水面上升3分米.这个圆锥的体积是多少立方分米?
15.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个直径6米的半圆形.
(1)搭建这个大棚大约要用多少平方米的塑料薄膜?
(2)大棚内的空间大约有多少立方米?
16.一个圆柱形水杯,底面直径10厘米,高40厘米,现在有10升的水倒入这个水杯中,可以倒满几杯?
17.一个圆柱形容器的底面半径是4分米,高是6分米,里面盛满水,倒进棱长是8分米的正方体容器内,水深是多少分米?
18.一卷透明胶带,它的外直径是5厘米,内直径是4厘米,胶带宽2厘米.这卷透明胶带的外大圆柱体积是多少立方厘米?内小圆柱体积是多少立方厘米?
参考答案:
1.每分钟压路的面积是18.84平方米,这个前轮一共重多9.42吨.
【详解】试题分析:(1)所压的路面是一个长方形平面,它的长就是压路机前进的米数,宽1.5米(已知),根据长方形面积计算公式,即可求出所压的面积.
(2)首先根据圆柱的体积公式:v=sh,求出压路机前轮的体积,再乘每立方米铁的质量即可.
解:(1)3.14×1×4×1.5,
=12.56×1.5,
=18.84(平方米);
(2)3.14×()2×1.5×8,
=3.14×0.25×1.5×8,
=1.1775×8,
=9.42(吨);
答:每分钟压路的面积是18.84平方米,这个前轮一共重多9.42吨.
点评:此题主要考查圆的周长公式、圆柱的体积公式的实际应用.
2.6.4厘米
【详解】试题分析:根据题意可知,容器A和B底面半径的比是3:4,那么两圆柱体容器的底面积比是9:16;又知道容器A和B的深度相等,高相等,所以容器A的体积是容器B体积的;由此列式解答.
解:(3.14×32)÷(3.14×42)
=(3.14×9)÷(3.14×16)
=28.26÷50.24
=;
1.2÷(﹣)
=1.2÷
=1.2×
=6.4(厘米);
答:B容器的深度是6.4厘米.
点评:此题解答的关键根据两个圆柱体的高相等,它们底面积的比等于底面半径的平方比,就是求出两个容器体积的比,;再根据已知比一个数少几分之几的数是多少,求这个数,用除法解答.
3.4:3
【详解】试题分析:如果以BC为底边,把纸片卷成一个圆柱,则圆柱的底面周长为4厘米,高为3厘米,体积为:V1=π×3;如果以AB为底边,把纸片卷成一个圆柱,则圆柱的底面周长为3厘米,高为4厘米,体积为:V2=π×4;由此写出V1与V2的比,化简比即可得出答案.
解:V1:V2=[π×3]:[π×4];
=[16×3]:[9×4];
=4:3;
答:V1:V2=4:3.
点评:此题主要考查圆柱的体积公式及化简比,关键要知道两次把长方形纸卷成圆柱的底面周长和高,代入公式表示出两个圆柱体积,化简比即可.
4.3厘米.
【详解】试题分析:由题意知,水面下降2.5厘米的水的体积就是这个圆锥形零件的体积,由此利用圆柱的体积=πr2h,计算出这个圆锥形零件的体积;再利用圆锥的高=圆锥的体积×3÷底面积进行解答.
解:下降2.5厘米的水的体积即这个圆锥形零件的体积为:
3.14×302×2.5,
=3.14×900×2.5,
=282.6×2.5,
=706.5(立方厘米);
所以圆锥形零件的高为:
706.5×3÷(3.14×152),
=2119.5÷706.5,
=3(厘米);
答:这个圆锥形零件的高是3厘米.
点评:此题考查了圆柱与圆锥的体积公式的灵活应用,这里根据下降的水的体积求得圆锥形零件的体积是本题的关键.再根据体积公式列式解答且不要漏了.
5.8厘米
【详解】试题分析:先求出圆柱体零件的体积,再求出圆柱体的底面半径,那底面积即可求出,最后即可求出圆柱体的高.
解:圆柱体的体积:1763.424÷7.8=226.08(立方厘米),
底面半径是:18.84÷3.14÷2=3(厘米),
底面积是:3.14×32=3.14×9=28.26(平方厘米),
高是:226.08÷28.26=8(厘米),
答:这个圆柱体的高是8厘米.
点评:此题主要考查了圆柱体的体积公式的灵活应用.
6.2米=20分米 6÷2=3(分米)
3×3×3.14×20×7.8=4408.56(千克)
【详解】略
7.(1)18.84÷3.14÷2=3(米)
3.14×32=28.26(平方米)
答:这个沙堆的占地面积是28.26平方米.
(2)28.26×1.2×÷3.6=3.14(米)
答:能装3.14米高.
【详解】略
8.3.14×(6÷2)2×6×1=169.56(立方分米)
169.56立方分米=169.56升
答:这个水桶能装水169.56千克.
【详解】略
9.(1)×3.14×42×3=50.24(cm3)
答:得到的圆锥的体积是50.24 cm3.
(2)3×4÷5=2.4(cm)
×3.14×2.42×5=30.144(cm3)
答:所得到的立体图形的体积是30.144 cm3.
【详解】略
10.(1)16.956平方米
(2)135.648千克
【分析】(1)根据圆柱的表面积=侧面积+底面积×2,求出一个圆柱的表面积乘10即可。
(2)求出油桶的容积的升数乘0.8即可。
【详解】(1)6÷2=3(分米)
(6×3.14×6+3×3×3.14×2)×10
=(113.04+56.52)×10
=169.56×10
=1695.6(平方分米)
=16.956平方米
答:制作10个这样的油桶至少需要16.956平方米的铁皮。
(2)3×3×3.14×6×0.8
=28.26×6×0.8
=169.56×0.8
=135.648(千克)
答:一个油桶能装油135.648千克。
【点睛】此题考查圆柱的表面积、体积相关应用。掌握其公式是解题关键。
11.122.46平方米
【详解】3.14× +3.14×6×5=122.46(平方米)
答:抹水泥面的面积是122.46平方米.
12.4396千克
【详解】粮囤的底面积:3.14×( )2=3.14(平方米)
粮囤的体积:3.14×18+3.14×0.6× =6.28(立方米)
粮食重量:700×6.28=4396(千克)
答:这个粮囤装粮4396千克.
13.58.7808千克
【详解】4厘米=0.4分米,2厘米=0.2分米,2米=20分米
内半径:0.4÷2=0.2(分米)
外半径:0.2+0.2=0.4(分米)
钢管体积:3.14×(0.42-0.22)×20=7.536(立方分米)
钢管重量:7.8×7.536=58.7808(千克)
答:这根钢管重58.7808千克.
14.48π
【详解】略
15.(1)69π (2)90π
【详解】略
16.3杯
【详解】3.14×(10÷2) ×40
=3.14×1000
=3140(立方厘米)
3140立方厘米=3.14升
10÷3.14≈3(杯〕
答:可以倒满3杯。
17.4.71分米
【分析】根据圆柱体积=底面积×高,求出圆柱容积,用圆柱容积÷正方体容器底面积即可。
【详解】3.14×4 ×6
=50.24×6
=301.44(立方分米)
301.44÷(8×8)
=301.44÷64
=4.71(分米)
答:水深是4.71分米。
【点睛】关键是掌握圆柱和长方体体积公式。
18.V外:39.25立方厘米 V内:25.12立方厘米
【分析】根据题意可知,利用圆柱体积公式:,代数解答即可。
【详解】3.14×(5÷2)×2
=3.14×6.25×2
=19.625×2
=39.25(立方厘米)
答:这卷透明胶带的外大圆柱体积是39.25立方厘米。
3.14×(4÷2)×2
=3.14×4×2
=25.12(立方厘米)
答:这卷透明胶带的内小圆柱体积是25.12立方厘米。
【点睛】此题主要考查学生对圆柱体积公式的实际应用解题能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
