第三单元解决问题的策略解决问题寒假预习小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第三单元解决问题的策略解决问题寒假预习小学数学六年级下册苏教版(含答案) | 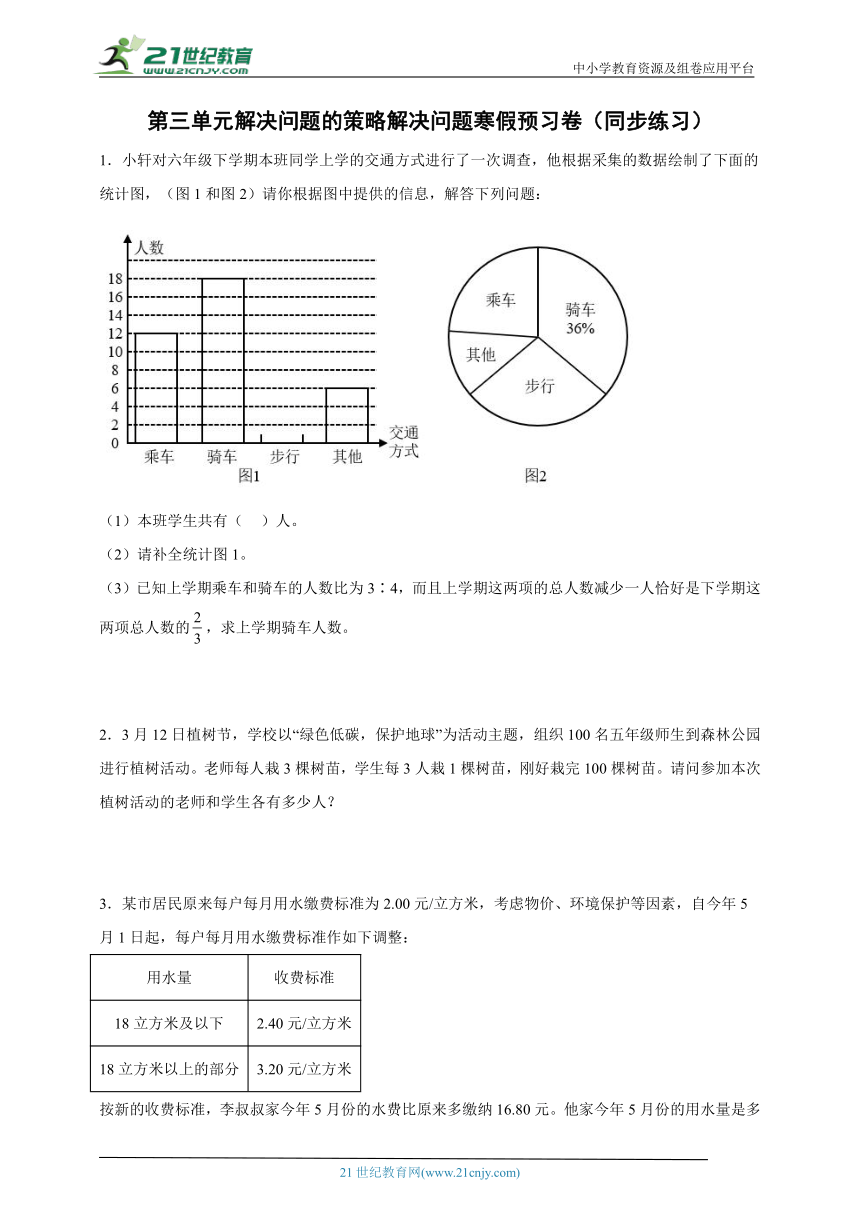 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 18:49:52 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第三单元解决问题的策略解决问题寒假预习卷(同步练习)
1.小轩对六年级下学期本班同学上学的交通方式进行了一次调查,他根据采集的数据绘制了下面的统计图,(图1和图2)请你根据图中提供的信息,解答下列问题:
(1)本班学生共有( )人。
(2)请补全统计图1。
(3)已知上学期乘车和骑车的人数比为3∶4,而且上学期这两项的总人数减少一人恰好是下学期这两项总人数的,求上学期骑车人数。
2.3月12日植树节,学校以“绿色低碳,保护地球”为活动主题,组织100名五年级师生到森林公园进行植树活动。老师每人栽3棵树苗,学生每3人栽1棵树苗,刚好栽完100棵树苗。请问参加本次植树活动的老师和学生各有多少人?
3.某市居民原来每户每月用水缴费标准为2.00元/立方米,考虑物价、环境保护等因素,自今年5月1日起,每户每月用水缴费标准作如下调整:
用水量 收费标准
18立方米及以下 2.40元/立方米
18立方米以上的部分 3.20元/立方米
按新的收费标准,李叔叔家今年5月份的水费比原来多缴纳16.80元。他家今年5月份的用水量是多少?
4.甲、乙两人同时从A地骑车到B地,经过10分钟,乙到达B地,甲距B地还有1200米。已知甲、乙两人骑车的平均速度比为2∶3,A、B两地相距多远?
5.驼鹿是某岛上狼的重要食物来源,从1965年至1975年,驼鹿的数量增加了,达到1200只,由于食物充足,狼的数量达到50只,不断增加的狼捕食了越来越多的驼鹿,到1980年,驼鹿的数量又减少到400只,同时狼的数量也急剧减少,与1975年数量比是2∶5。
(1)1965年至1975年之前,驼鹿的数量多少只?
(2)1980年狼的数量是多少只?
6.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只,如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
7.小明在家学做小厨师,下面是他必做的一些事情和做每件事情所需的时间。
怎样安排才能在最短的时间内吃上饭菜?用你喜欢的方式表达。
8.中国空间站建设凝聚了许多科研工作者的心血与汗水,火箭研发中心、飞船研发中心、材料研发中心都有许多科研工作者。其中火箭研发中心有160人,关于这三个研发中心的科研工作者人数还有以下的信息,请选择合适的信息解答问题。
①火箭研发中心的人数是总人数的;
②飞船研发中心、火箭研发中心两个中心的人数比是3∶4;
③材料研发中心人数比飞船研发中心人数多;
④材料研发中心人数比总人数的40%多8人。
请选择合适信息,计算材料研发中心有科技工作者多少人?
9.“冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物,“冰墩墩”是以熊猫为原型设计的,“雪容融”是以灯笼为原型设计的。某单位花费5280元购买了同一型号的“冰墩墩”和“雪容融”毛绒玩偶共35个,作为冬奥知识竞赛的奖品。“冰墩墩”毛绒玩偶192元一个,“雪容融”毛线玩偶96元一个。该单位购头“冰墩墩”和“雪容融”玩偶各多少个?
10.张叔叔把车开到停车场,车子停4个小时,如果按停车收费标准,应交停车费多少元?李叔叔也在这个停车场停车,他交的停车费是33元钱,李叔叔停车多长时间?
停车时间 收费标准
3小时 5元/时
超过3小时 超出部分每小时优惠20%
11.全国义务教育劳动课程标准出台以后,让学生学会做家务劳动成为新的热门话题。某校在端午节来临之际,组织学生进行包棕子比赛,四、五、六年级代表队完成粽子的个数比为4∶5∶6,已知四年级代表队包了60个棕子,请你帮忙计算这三个代表队一共包了多少个棕子?
12.一种混泥土是按水泥∶黄沙∶石子的配方配制。
(1)要配制120吨这样的混泥土,三种材料各需要多少吨?
(2)如果这三种材料各15吨,要配制这种混泥土,当黄沙全部用完时,水泥还剩多少吨?石子要增加多少吨?
13.甲、乙两车同时从两地相对开出,相遇时甲车比乙车多行。如果甲、乙两车的速度比是,速度之和是120千米时,则两车从出发到相遇共经过多长时间?
14.皓午看一本小说,看了3天后他发现已经看的页数与还剩的页数比是,如果再看25页就正好看了一半,这本书有多少页?
15.张伯伯摆地摊卖苹果和香蕉,每袋苹果25元,每袋香蕉30元。某天张伯伯卖掉了20袋水果,一共卖了540元,则苹果和香蕉各卖出了多少袋?(用你喜欢的方式解答)
16.一场篮球赛的门票有两种,一种票价是40元一张,另一种是50元一张,李老师买了10张门票,一共用去430元,两种门票各买了多少张?
17.甲、乙两个煤仓储煤量的比为4∶5,从甲仓运出25%放入乙仓,这时乙仓储煤72吨。乙仓原来储煤多少吨?
18.红星车辆厂今年五月份共生产电动三轮车和电动四轮车160辆,组装时一共用了570个同样的车轮。红星车辆厂五月份分别生产电动三轮车和电动四轮车多少辆?
19.刘大伯家将3680平方米的菜地分成四块分别种辣椒、黄瓜、茄子和西红柿。已知辣椒地的面积是800平方米,黄瓜地的面积比西红柿多120平方米,茄子地的面积比西红柿少150平方米。黄瓜、茄子和西红柿菜地的面积各是多少平方米?
20.甲乙两种衫衣的原价相同,现在甲种衬衣按六折销售,乙种衬衣按七折销售。王叔叔用156元购得这两种衫衣各一件。两种衬衣的原价各是多少元?
参考答案:
1.(1)50;(2)见详解;(3)12人
【分析】(1)已知骑车人数占总人数的36%,骑车人数有18人,根据已知一个数的百分之几是多少,求这个数用除法解答,可用18÷36%求得总人数;
(2)步行的人数=总人数-乘车的人数-骑车的人数-其他方式的人数,据此补全统计图;
(3)把下学期乘车和骑车人数看作单位“1”,则用(12+18)×+1可得上学期这两项的总人数,已知上学期乘车和骑车的人数比为3∶4,把上学期乘车人数看作3份,骑车的人数看作4份,则用上学期这两项的总人数除以(3+4)份,即可得每份是多少,进而求出4份是多少。
【详解】(1)18÷36%=50(人)
本班学生共有50人。
(2)步行的人数:50-12-18-6
=20-6
=14(人)
如图:
(3)(12+18)×
=30×
=20(人)
20+1=21(人)
21÷(3+4)×4
=21÷7×4
=12(人)
答:上学期骑车有12人。
【点睛】本题主要考查了对扇形统计图和条形统计图的分析能力。
2.老师25人;学生75人
【分析】把参加植树活动的老师人数设为未知数,学生人数=总人数-老师人数,学生每3人栽1棵树苗,则一人栽1÷3=棵树苗,等量关系式:老师的植树棵数+学生的植树棵数=植树总棵数,据此解答。
【详解】解:设参加植树活动的老师有x人,则参加植树活动的学生有(100-x)人。
3x+(100-x)=100
3x+-x=100
3x-x=100-
x=
x=÷
x=25
学生:100-25=75(人)
答:参加植树活动的老师有25人,参加植树活动的学生有75人。
【点睛】准确设出未知数并找出等量关系式是解答题目的关键。
3.26立方米
【分析】根据题意,多缴的16.80元,可分为18立方米以下,和18立方米以上两部分多缴的,分别求出现在比原来每立方米多缴的钱数,就可以求出18立方米以上部分是多少立方米,再与18立方米合并起来即可。
【详解】18立方米以下,每立方米多缴:2.40-2.00=0.4(元)
18立方米一共多缴:18×0.40=7.2(元)
18立方米以上每立方米多缴:3.20-2.00=1.2(元)
18立方米以上的用水量是:
(16.8-7.2)÷1.2
=9.6÷1.2
=8(立方米)
这个月的用水量是:18+8=26(立方米)
答:他家今年5月份的用水量是26立方米。
【点睛】此题数量关系比较复杂,解答时首先弄清现在比原来多缴的钱,要分成两部分计算。
4.3600米
【分析】根据题意,甲、乙两人骑车的平均速度比为2∶3,经过10分钟,乙到达B地,甲距B地还有1200米,可以找出等量关系是:甲的速度×10分钟+1200=乙的速度×10分钟。据此解答即可。
【详解】解:根据甲、乙两人骑车的平均速度比为2∶3,设甲速度为2x米/分钟,乙的速度为3x米/分钟。
2x×10+1200=3x×10
20x+1200=30x
10x=1200
x=120
乙的速度为:3x=3×120=360(米/分钟)
A、B两地相距:360×10=3600(米)
答:A、B两地相距3600米。
【点睛】本题考查了行程问题,关键是得出等量关系:甲的速度×10分钟+1200=乙的速度×10分钟。
5.(1)750只;
(2)20只
【分析】(1)设1965年至1975年之前,驼鹿的数量x只,根据等量关系式:1965年至1975年之前,驼鹿的数量×(1+)=1200,据此列方程解答即可;
(2)由题意可知,1975年狼的数量达到50只,1980年狼的数量与1975年狼的数量的比是2∶5,据此列比例解答即可。
【详解】(1)解:设1965年至1975年之前,驼鹿的数量x只。
x=750
答:1965年至1975年之前,驼鹿的数量750只。
(2)解:设1980年狼的数量是x只。
2∶5=x∶50
5x=2×50
5x=100
x=20
答:1980年狼的数量是20只。
【点睛】本题考查用方程解决实际问题和比的应用,明确等量关系是解题的关键。
6.蜘蛛10只;蚱蜢15只
【分析】设蜘蛛x只,则蚱蜢有(25-x)只,根据蜘蛛数量×腿数+蚱蜢数量×腿数=总腿数,列出方程求出x的值是蜘蛛数量,总数量-蜘蛛数量=蚱蜢数量。
【详解】解:设蜘蛛x只。
8x+(25-x)×6=170
8x+150-6x=170
2x+150-150=170-150
2x÷2=20÷2
x=10
25-10=15(只)
答:蜘蛛有10只,蚱蜢有15只。
【点睛】用方程解决问题的关键是找到等量关系,本题也可以用假设法进行解答。
7.小明先淘米,再用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜。
【分析】小明先淘米,用时4.5分钟;接着,用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜三件事,不过炒菜炒了20-4.5-5=10.5(分钟)后饭熟了,小明继续炒菜1.5分钟,菜熟了;据此解答即可。
【详解】小明先淘米,接着,用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜三件事,不过炒菜炒了20-4.5-5=10.5(分钟)后饭熟了,小明继续炒菜1.5分钟,菜熟了。
2.5+20+(4.5+5+12-20)
=2.5+20+1.5
=24(分钟)
答:小明先淘米,再用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜。
【点睛】本题属于合理安排时间问题,要奔着既节约时间又不使每道工序相矛盾进行解答。
8.①④,200人。
【分析】选择①④,用火箭研发中心的人数除以火箭研发中心的人数占总人数的分率,得出总人数,再乘40%,最后加8人,即可得材料研发中心有科技工作者的人数。
【详解】①④
160÷×40%+8
=480×40%+8
=192+8
=200(人)
答:材料研发中心有科技工作者200人。
【点睛】本题主要考查了比的应用,已知一个数的几分之几是多少,求这个数,用除法计算;已知一个数,求它的百分之几是多少,用乘法计算。
9.冰墩墩20个,雪容融15个
【分析】假设35个都是“冰墩墩”,是用“冰墩墩”毛绒玩偶的单价乘35,得出35个冰墩墩"毛绒玩偶的价钱,再减花的总钱数,除以1个“冰墩墩”毛绒玩偶比1个雪容融“毛绒玩偶多花的钱数,即可得“雪容融“毛绒玩偶的个数,再求“冰墩墩”毛绒玩偶的个数即可。
【详解】方法一:假设全部都是“冰墩墩”。
192×35-5280
=6720-5280
=1440(元)
雪容融:1440÷(192-96)
=1440÷96
=15(个)
冰墩墩:35-15=20(个)
答:冰墩墩买来20个,雪容融买来15个。
方法二:假设全部都是“雪容融”。
5280-96×35
=5280-3360
=1920(元)
冰墩墩:1920÷(192-96)
=1920÷96
=20(个)
雪容融:35-20=15(个)
答:冰墩墩买来20个,雪容融买来15个。
【点睛】本题主要考查了用假设的策略来解决实际问题的能力。
10.19元;7.5小时
【分析】用总时间减去3小时,求出超出的时间,乘超出3小时的单价,超出部分每小时优惠20%,即是不超出部分的(1-20%),即可求出超出3小时的总价,再加上3小时以内的价钱,即可求出应付停车费多少元;用李叔叔交的钱数减3小时以内的价钱,再除以超出3小时的单价,得出超出的时间,最后加3,即可得李叔叔停车多长时间。
【详解】(4-3)×5×(1-20%)+3×5
=1×5×0.8+15
=4+15
=19(元)
答:应交停车费19元。
(33-3×5)÷[5×(1-20%)]+3
=(33-15)÷[5×0.8]+3
=18÷4+3
=4.5+3
=7.5(小时)
答:李叔叔停车7.5小时。
【点睛】本题考查百分数乘法的计算及应用。理解用“分段计费”法解决此类问题,注意计算的准确性。
11.225个
【分析】四、五、六年级代表队完成粽子的个数比为4∶5∶6,把四年级代表队完成粽子的个数看作4份,五年级代表队完成粽子的个数看作5份,六年级代表队完成粽子的个数看作6份,三个代表队一共(4+5+6)份,用四年级代表队包的个数除以4,得出1份的个数,再求这三个代表队一共包了多少个粽子。
【详解】60÷4×(4+5+6)
=15×15
=225(个)
答:这三个代表队一共包了225个粽子。
【点睛】本题主要考查了比的应用,关键是得出1份的个数。
12.(1)水泥24吨;黄沙36吨;石子60吨。
(2)5吨;10吨
【分析】(1)先求出每份混凝土中水泥、黄沙、石子的份数总和,再求出各自所占的分率,用120乘分率,即可解答;
(2)用15除以3求出每1份黄沙多少吨,根据按比例分配问题,再求出所需用的水泥和石子吨数,再求出水泥还剩多少吨,石子要增加多少吨。
【详解】(1)
(吨)
(吨)
(吨)
答:需要水泥24吨,黄沙36吨,石子60吨。
(2)(吨)
水泥剩:
(吨)
石子缺:
(吨)
答:水泥还剩5吨,需要增加石子10吨。
【点睛】本题主要考查比的应用,第(2)题中求出1份所对应的量是解题的关键。
13.8小时
【分析】时间相同,路程比等于速度比。由此可以得出,甲、乙两车的路程比也是 7∶5 ,所以甲车路程是7份,乙车路程是5份,总路程就是12份。求出160千米所对应的分率,用分数除法即可求出总路程,再用总路程除以速度和,得出相遇时间。
【详解】
(千米)
(小时)
答:两车从出发到相遇共经过8小时。
【点睛】根据速度比求出路程比,再求出160千米所对应的分率是解题的关键。
14.450页
【分析】把这本书的页数看作单位“1”,已经看的页数为4份,还剩的页数为5份。已经看的占总页数的。求出25页所占的分率,再用分数除法解题即可。
【详解】
=
=25×18
=450(页)
答:这本书有450页。
【点睛】本题主要考查分数除法的意义。求出25页所占的分率是解题的关键。
15.苹果12袋;香蕉8袋
【分析】本题可以采用鸡兔同笼问题的方法来解决,假设全是卖的苹果(或者全是卖的香蕉),差价部分就是把卖出的香蕉看成苹果(或卖出的苹果看成香蕉)造成的。也可以采用设未知数,列方程来解答。
【详解】方法一:假设卖掉的全是苹果。
(元)
香蕉:
=40÷5
=8(袋)
苹果:(袋)
答:卖出苹果12袋,卖出香蕉8袋。
方法二:假设卖掉的全是香蕉。
(元)
苹果:
=60÷5
=12(袋)
香蕉:(袋)
答:卖出苹果12袋,卖出香蕉8袋。
方法三:解:设卖出苹果x袋,则卖出香蕉袋。
答:卖出苹果12袋,卖出香蕉8袋。
【点睛】本题属于鸡兔同笼问题,解决此类问题的关键是用假设法进行分析,进而得出结论,也可以采用方程进行解答。
16.7张;3张
【分析】设一种门票买了x张,则另一种买了(10-x)张,根据单价×数量=总价,一种门票数量×单价+另一种门票数量×单价=430,列出方程求出x的值是一种门票数量,10-一种门票数量=另一种门票数量,据此分析。
【详解】解:设一种门票买了x张,则另一种买了(10-x)张。
40x+50(10-x)=430
40x+500-50x=430
10x÷10=70÷10
x=7
10-7=3(张)
答:两种门票各买了7张、3张。
【点睛】用方程解决问题的关键是找到等量关系,本题也可以用假设法解答。
17.60吨
【分析】把原来甲仓储煤的吨数看作4份,则乙仓储煤的吨数就是5份,甲仓中1份占25%=,即甲仓运出1份放入乙仓,这时乙仓储煤就是(5+1)份,先用除法求出1份的吨数,再用乘法求出5份的吨数,即乙仓原来储煤吨数。
【详解】设原来甲仓储煤的吨数看作4份,则乙仓储煤的吨数就是5份
25%=,即甲仓运出1份放入已仓,此时乙仓储煤就是(5+1)份
72÷(5+1)×5
=72÷6×5
=60(吨)
答:乙仓原来储煤60吨。
【点睛】关键是根据题意,求出甲、乙两仓各储煤多少份,从甲仓运出25%放入乙仓,甲仓运出几份放入乙仓,此时乙仓是多少份。
18.三轮车70辆,电动四轮车90辆
【分析】根据题意,假设都是四轮车,则轮子应有160×4=640(个),比实际多640﹣570=70(个),每辆三轮比四轮相差4﹣3=1(个)轮子,所以三轮车有70÷1=70(辆);再根据总辆数求四轮车的辆数即可。
【解答】解:(160×4﹣570)÷(4﹣3)
=70÷1
=70(辆)
160﹣70=90(辆)
答:红星车辆厂五月份分别生产电动三轮车70辆,电动四轮车90辆。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
19.黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米
【分析】用3680减去辣椒地的面积就是黄瓜、茄子和西红柿的面积和,用黄瓜、茄子和西红柿的面积和减去黄瓜地的面积比西红柿多的120平方米,再加上茄子地的面积比西红柿少的150平方米,就相当于3块西红柿地的面积,再除以3就是1块西红柿地的面积,进一步求出黄瓜地和茄子地的面积。
【详解】3680﹣800=2880(平方米)
(2880﹣120+150)÷3
=2910÷3
=970(平方米)
970+120=1090(平方米)
970﹣150=820(平方米)
答:黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米。
【点睛】解决此题的关键是求出西红柿地的面积。
20.120元
【分析】根据题意,设两种衬衣的原价都是x元,则甲衬衣的售价为60%x,乙衬衣的售价为70%x,列方程为:60%x+70%x=156,解方程即可。
【详解】解:设两种衬衣的原价都是x元,根据题意列方程如下:
60%x+70%x=156
1.3x=156
x=120
答:两种衬衣的原价是120元。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:甲种衬衣的现价+乙种衬衣的现价=156,进而列出方程是解答此类问题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元解决问题的策略解决问题寒假预习卷(同步练习)
1.小轩对六年级下学期本班同学上学的交通方式进行了一次调查,他根据采集的数据绘制了下面的统计图,(图1和图2)请你根据图中提供的信息,解答下列问题:
(1)本班学生共有( )人。
(2)请补全统计图1。
(3)已知上学期乘车和骑车的人数比为3∶4,而且上学期这两项的总人数减少一人恰好是下学期这两项总人数的,求上学期骑车人数。
2.3月12日植树节,学校以“绿色低碳,保护地球”为活动主题,组织100名五年级师生到森林公园进行植树活动。老师每人栽3棵树苗,学生每3人栽1棵树苗,刚好栽完100棵树苗。请问参加本次植树活动的老师和学生各有多少人?
3.某市居民原来每户每月用水缴费标准为2.00元/立方米,考虑物价、环境保护等因素,自今年5月1日起,每户每月用水缴费标准作如下调整:
用水量 收费标准
18立方米及以下 2.40元/立方米
18立方米以上的部分 3.20元/立方米
按新的收费标准,李叔叔家今年5月份的水费比原来多缴纳16.80元。他家今年5月份的用水量是多少?
4.甲、乙两人同时从A地骑车到B地,经过10分钟,乙到达B地,甲距B地还有1200米。已知甲、乙两人骑车的平均速度比为2∶3,A、B两地相距多远?
5.驼鹿是某岛上狼的重要食物来源,从1965年至1975年,驼鹿的数量增加了,达到1200只,由于食物充足,狼的数量达到50只,不断增加的狼捕食了越来越多的驼鹿,到1980年,驼鹿的数量又减少到400只,同时狼的数量也急剧减少,与1975年数量比是2∶5。
(1)1965年至1975年之前,驼鹿的数量多少只?
(2)1980年狼的数量是多少只?
6.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只,如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
7.小明在家学做小厨师,下面是他必做的一些事情和做每件事情所需的时间。
怎样安排才能在最短的时间内吃上饭菜?用你喜欢的方式表达。
8.中国空间站建设凝聚了许多科研工作者的心血与汗水,火箭研发中心、飞船研发中心、材料研发中心都有许多科研工作者。其中火箭研发中心有160人,关于这三个研发中心的科研工作者人数还有以下的信息,请选择合适的信息解答问题。
①火箭研发中心的人数是总人数的;
②飞船研发中心、火箭研发中心两个中心的人数比是3∶4;
③材料研发中心人数比飞船研发中心人数多;
④材料研发中心人数比总人数的40%多8人。
请选择合适信息,计算材料研发中心有科技工作者多少人?
9.“冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物,“冰墩墩”是以熊猫为原型设计的,“雪容融”是以灯笼为原型设计的。某单位花费5280元购买了同一型号的“冰墩墩”和“雪容融”毛绒玩偶共35个,作为冬奥知识竞赛的奖品。“冰墩墩”毛绒玩偶192元一个,“雪容融”毛线玩偶96元一个。该单位购头“冰墩墩”和“雪容融”玩偶各多少个?
10.张叔叔把车开到停车场,车子停4个小时,如果按停车收费标准,应交停车费多少元?李叔叔也在这个停车场停车,他交的停车费是33元钱,李叔叔停车多长时间?
停车时间 收费标准
3小时 5元/时
超过3小时 超出部分每小时优惠20%
11.全国义务教育劳动课程标准出台以后,让学生学会做家务劳动成为新的热门话题。某校在端午节来临之际,组织学生进行包棕子比赛,四、五、六年级代表队完成粽子的个数比为4∶5∶6,已知四年级代表队包了60个棕子,请你帮忙计算这三个代表队一共包了多少个棕子?
12.一种混泥土是按水泥∶黄沙∶石子的配方配制。
(1)要配制120吨这样的混泥土,三种材料各需要多少吨?
(2)如果这三种材料各15吨,要配制这种混泥土,当黄沙全部用完时,水泥还剩多少吨?石子要增加多少吨?
13.甲、乙两车同时从两地相对开出,相遇时甲车比乙车多行。如果甲、乙两车的速度比是,速度之和是120千米时,则两车从出发到相遇共经过多长时间?
14.皓午看一本小说,看了3天后他发现已经看的页数与还剩的页数比是,如果再看25页就正好看了一半,这本书有多少页?
15.张伯伯摆地摊卖苹果和香蕉,每袋苹果25元,每袋香蕉30元。某天张伯伯卖掉了20袋水果,一共卖了540元,则苹果和香蕉各卖出了多少袋?(用你喜欢的方式解答)
16.一场篮球赛的门票有两种,一种票价是40元一张,另一种是50元一张,李老师买了10张门票,一共用去430元,两种门票各买了多少张?
17.甲、乙两个煤仓储煤量的比为4∶5,从甲仓运出25%放入乙仓,这时乙仓储煤72吨。乙仓原来储煤多少吨?
18.红星车辆厂今年五月份共生产电动三轮车和电动四轮车160辆,组装时一共用了570个同样的车轮。红星车辆厂五月份分别生产电动三轮车和电动四轮车多少辆?
19.刘大伯家将3680平方米的菜地分成四块分别种辣椒、黄瓜、茄子和西红柿。已知辣椒地的面积是800平方米,黄瓜地的面积比西红柿多120平方米,茄子地的面积比西红柿少150平方米。黄瓜、茄子和西红柿菜地的面积各是多少平方米?
20.甲乙两种衫衣的原价相同,现在甲种衬衣按六折销售,乙种衬衣按七折销售。王叔叔用156元购得这两种衫衣各一件。两种衬衣的原价各是多少元?
参考答案:
1.(1)50;(2)见详解;(3)12人
【分析】(1)已知骑车人数占总人数的36%,骑车人数有18人,根据已知一个数的百分之几是多少,求这个数用除法解答,可用18÷36%求得总人数;
(2)步行的人数=总人数-乘车的人数-骑车的人数-其他方式的人数,据此补全统计图;
(3)把下学期乘车和骑车人数看作单位“1”,则用(12+18)×+1可得上学期这两项的总人数,已知上学期乘车和骑车的人数比为3∶4,把上学期乘车人数看作3份,骑车的人数看作4份,则用上学期这两项的总人数除以(3+4)份,即可得每份是多少,进而求出4份是多少。
【详解】(1)18÷36%=50(人)
本班学生共有50人。
(2)步行的人数:50-12-18-6
=20-6
=14(人)
如图:
(3)(12+18)×
=30×
=20(人)
20+1=21(人)
21÷(3+4)×4
=21÷7×4
=12(人)
答:上学期骑车有12人。
【点睛】本题主要考查了对扇形统计图和条形统计图的分析能力。
2.老师25人;学生75人
【分析】把参加植树活动的老师人数设为未知数,学生人数=总人数-老师人数,学生每3人栽1棵树苗,则一人栽1÷3=棵树苗,等量关系式:老师的植树棵数+学生的植树棵数=植树总棵数,据此解答。
【详解】解:设参加植树活动的老师有x人,则参加植树活动的学生有(100-x)人。
3x+(100-x)=100
3x+-x=100
3x-x=100-
x=
x=÷
x=25
学生:100-25=75(人)
答:参加植树活动的老师有25人,参加植树活动的学生有75人。
【点睛】准确设出未知数并找出等量关系式是解答题目的关键。
3.26立方米
【分析】根据题意,多缴的16.80元,可分为18立方米以下,和18立方米以上两部分多缴的,分别求出现在比原来每立方米多缴的钱数,就可以求出18立方米以上部分是多少立方米,再与18立方米合并起来即可。
【详解】18立方米以下,每立方米多缴:2.40-2.00=0.4(元)
18立方米一共多缴:18×0.40=7.2(元)
18立方米以上每立方米多缴:3.20-2.00=1.2(元)
18立方米以上的用水量是:
(16.8-7.2)÷1.2
=9.6÷1.2
=8(立方米)
这个月的用水量是:18+8=26(立方米)
答:他家今年5月份的用水量是26立方米。
【点睛】此题数量关系比较复杂,解答时首先弄清现在比原来多缴的钱,要分成两部分计算。
4.3600米
【分析】根据题意,甲、乙两人骑车的平均速度比为2∶3,经过10分钟,乙到达B地,甲距B地还有1200米,可以找出等量关系是:甲的速度×10分钟+1200=乙的速度×10分钟。据此解答即可。
【详解】解:根据甲、乙两人骑车的平均速度比为2∶3,设甲速度为2x米/分钟,乙的速度为3x米/分钟。
2x×10+1200=3x×10
20x+1200=30x
10x=1200
x=120
乙的速度为:3x=3×120=360(米/分钟)
A、B两地相距:360×10=3600(米)
答:A、B两地相距3600米。
【点睛】本题考查了行程问题,关键是得出等量关系:甲的速度×10分钟+1200=乙的速度×10分钟。
5.(1)750只;
(2)20只
【分析】(1)设1965年至1975年之前,驼鹿的数量x只,根据等量关系式:1965年至1975年之前,驼鹿的数量×(1+)=1200,据此列方程解答即可;
(2)由题意可知,1975年狼的数量达到50只,1980年狼的数量与1975年狼的数量的比是2∶5,据此列比例解答即可。
【详解】(1)解:设1965年至1975年之前,驼鹿的数量x只。
x=750
答:1965年至1975年之前,驼鹿的数量750只。
(2)解:设1980年狼的数量是x只。
2∶5=x∶50
5x=2×50
5x=100
x=20
答:1980年狼的数量是20只。
【点睛】本题考查用方程解决实际问题和比的应用,明确等量关系是解题的关键。
6.蜘蛛10只;蚱蜢15只
【分析】设蜘蛛x只,则蚱蜢有(25-x)只,根据蜘蛛数量×腿数+蚱蜢数量×腿数=总腿数,列出方程求出x的值是蜘蛛数量,总数量-蜘蛛数量=蚱蜢数量。
【详解】解:设蜘蛛x只。
8x+(25-x)×6=170
8x+150-6x=170
2x+150-150=170-150
2x÷2=20÷2
x=10
25-10=15(只)
答:蜘蛛有10只,蚱蜢有15只。
【点睛】用方程解决问题的关键是找到等量关系,本题也可以用假设法进行解答。
7.小明先淘米,再用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜。
【分析】小明先淘米,用时4.5分钟;接着,用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜三件事,不过炒菜炒了20-4.5-5=10.5(分钟)后饭熟了,小明继续炒菜1.5分钟,菜熟了;据此解答即可。
【详解】小明先淘米,接着,用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜三件事,不过炒菜炒了20-4.5-5=10.5(分钟)后饭熟了,小明继续炒菜1.5分钟,菜熟了。
2.5+20+(4.5+5+12-20)
=2.5+20+1.5
=24(分钟)
答:小明先淘米,再用电饭锅煮饭,在煮饭的同时,洗菜,切菜,和炒菜。
【点睛】本题属于合理安排时间问题,要奔着既节约时间又不使每道工序相矛盾进行解答。
8.①④,200人。
【分析】选择①④,用火箭研发中心的人数除以火箭研发中心的人数占总人数的分率,得出总人数,再乘40%,最后加8人,即可得材料研发中心有科技工作者的人数。
【详解】①④
160÷×40%+8
=480×40%+8
=192+8
=200(人)
答:材料研发中心有科技工作者200人。
【点睛】本题主要考查了比的应用,已知一个数的几分之几是多少,求这个数,用除法计算;已知一个数,求它的百分之几是多少,用乘法计算。
9.冰墩墩20个,雪容融15个
【分析】假设35个都是“冰墩墩”,是用“冰墩墩”毛绒玩偶的单价乘35,得出35个冰墩墩"毛绒玩偶的价钱,再减花的总钱数,除以1个“冰墩墩”毛绒玩偶比1个雪容融“毛绒玩偶多花的钱数,即可得“雪容融“毛绒玩偶的个数,再求“冰墩墩”毛绒玩偶的个数即可。
【详解】方法一:假设全部都是“冰墩墩”。
192×35-5280
=6720-5280
=1440(元)
雪容融:1440÷(192-96)
=1440÷96
=15(个)
冰墩墩:35-15=20(个)
答:冰墩墩买来20个,雪容融买来15个。
方法二:假设全部都是“雪容融”。
5280-96×35
=5280-3360
=1920(元)
冰墩墩:1920÷(192-96)
=1920÷96
=20(个)
雪容融:35-20=15(个)
答:冰墩墩买来20个,雪容融买来15个。
【点睛】本题主要考查了用假设的策略来解决实际问题的能力。
10.19元;7.5小时
【分析】用总时间减去3小时,求出超出的时间,乘超出3小时的单价,超出部分每小时优惠20%,即是不超出部分的(1-20%),即可求出超出3小时的总价,再加上3小时以内的价钱,即可求出应付停车费多少元;用李叔叔交的钱数减3小时以内的价钱,再除以超出3小时的单价,得出超出的时间,最后加3,即可得李叔叔停车多长时间。
【详解】(4-3)×5×(1-20%)+3×5
=1×5×0.8+15
=4+15
=19(元)
答:应交停车费19元。
(33-3×5)÷[5×(1-20%)]+3
=(33-15)÷[5×0.8]+3
=18÷4+3
=4.5+3
=7.5(小时)
答:李叔叔停车7.5小时。
【点睛】本题考查百分数乘法的计算及应用。理解用“分段计费”法解决此类问题,注意计算的准确性。
11.225个
【分析】四、五、六年级代表队完成粽子的个数比为4∶5∶6,把四年级代表队完成粽子的个数看作4份,五年级代表队完成粽子的个数看作5份,六年级代表队完成粽子的个数看作6份,三个代表队一共(4+5+6)份,用四年级代表队包的个数除以4,得出1份的个数,再求这三个代表队一共包了多少个粽子。
【详解】60÷4×(4+5+6)
=15×15
=225(个)
答:这三个代表队一共包了225个粽子。
【点睛】本题主要考查了比的应用,关键是得出1份的个数。
12.(1)水泥24吨;黄沙36吨;石子60吨。
(2)5吨;10吨
【分析】(1)先求出每份混凝土中水泥、黄沙、石子的份数总和,再求出各自所占的分率,用120乘分率,即可解答;
(2)用15除以3求出每1份黄沙多少吨,根据按比例分配问题,再求出所需用的水泥和石子吨数,再求出水泥还剩多少吨,石子要增加多少吨。
【详解】(1)
(吨)
(吨)
(吨)
答:需要水泥24吨,黄沙36吨,石子60吨。
(2)(吨)
水泥剩:
(吨)
石子缺:
(吨)
答:水泥还剩5吨,需要增加石子10吨。
【点睛】本题主要考查比的应用,第(2)题中求出1份所对应的量是解题的关键。
13.8小时
【分析】时间相同,路程比等于速度比。由此可以得出,甲、乙两车的路程比也是 7∶5 ,所以甲车路程是7份,乙车路程是5份,总路程就是12份。求出160千米所对应的分率,用分数除法即可求出总路程,再用总路程除以速度和,得出相遇时间。
【详解】
(千米)
(小时)
答:两车从出发到相遇共经过8小时。
【点睛】根据速度比求出路程比,再求出160千米所对应的分率是解题的关键。
14.450页
【分析】把这本书的页数看作单位“1”,已经看的页数为4份,还剩的页数为5份。已经看的占总页数的。求出25页所占的分率,再用分数除法解题即可。
【详解】
=
=25×18
=450(页)
答:这本书有450页。
【点睛】本题主要考查分数除法的意义。求出25页所占的分率是解题的关键。
15.苹果12袋;香蕉8袋
【分析】本题可以采用鸡兔同笼问题的方法来解决,假设全是卖的苹果(或者全是卖的香蕉),差价部分就是把卖出的香蕉看成苹果(或卖出的苹果看成香蕉)造成的。也可以采用设未知数,列方程来解答。
【详解】方法一:假设卖掉的全是苹果。
(元)
香蕉:
=40÷5
=8(袋)
苹果:(袋)
答:卖出苹果12袋,卖出香蕉8袋。
方法二:假设卖掉的全是香蕉。
(元)
苹果:
=60÷5
=12(袋)
香蕉:(袋)
答:卖出苹果12袋,卖出香蕉8袋。
方法三:解:设卖出苹果x袋,则卖出香蕉袋。
答:卖出苹果12袋,卖出香蕉8袋。
【点睛】本题属于鸡兔同笼问题,解决此类问题的关键是用假设法进行分析,进而得出结论,也可以采用方程进行解答。
16.7张;3张
【分析】设一种门票买了x张,则另一种买了(10-x)张,根据单价×数量=总价,一种门票数量×单价+另一种门票数量×单价=430,列出方程求出x的值是一种门票数量,10-一种门票数量=另一种门票数量,据此分析。
【详解】解:设一种门票买了x张,则另一种买了(10-x)张。
40x+50(10-x)=430
40x+500-50x=430
10x÷10=70÷10
x=7
10-7=3(张)
答:两种门票各买了7张、3张。
【点睛】用方程解决问题的关键是找到等量关系,本题也可以用假设法解答。
17.60吨
【分析】把原来甲仓储煤的吨数看作4份,则乙仓储煤的吨数就是5份,甲仓中1份占25%=,即甲仓运出1份放入乙仓,这时乙仓储煤就是(5+1)份,先用除法求出1份的吨数,再用乘法求出5份的吨数,即乙仓原来储煤吨数。
【详解】设原来甲仓储煤的吨数看作4份,则乙仓储煤的吨数就是5份
25%=,即甲仓运出1份放入已仓,此时乙仓储煤就是(5+1)份
72÷(5+1)×5
=72÷6×5
=60(吨)
答:乙仓原来储煤60吨。
【点睛】关键是根据题意,求出甲、乙两仓各储煤多少份,从甲仓运出25%放入乙仓,甲仓运出几份放入乙仓,此时乙仓是多少份。
18.三轮车70辆,电动四轮车90辆
【分析】根据题意,假设都是四轮车,则轮子应有160×4=640(个),比实际多640﹣570=70(个),每辆三轮比四轮相差4﹣3=1(个)轮子,所以三轮车有70÷1=70(辆);再根据总辆数求四轮车的辆数即可。
【解答】解:(160×4﹣570)÷(4﹣3)
=70÷1
=70(辆)
160﹣70=90(辆)
答:红星车辆厂五月份分别生产电动三轮车70辆,电动四轮车90辆。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
19.黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米
【分析】用3680减去辣椒地的面积就是黄瓜、茄子和西红柿的面积和,用黄瓜、茄子和西红柿的面积和减去黄瓜地的面积比西红柿多的120平方米,再加上茄子地的面积比西红柿少的150平方米,就相当于3块西红柿地的面积,再除以3就是1块西红柿地的面积,进一步求出黄瓜地和茄子地的面积。
【详解】3680﹣800=2880(平方米)
(2880﹣120+150)÷3
=2910÷3
=970(平方米)
970+120=1090(平方米)
970﹣150=820(平方米)
答:黄瓜地的面积是1090平方米,茄子地的面积是820平方米,西红柿地的面积是970平方米。
【点睛】解决此题的关键是求出西红柿地的面积。
20.120元
【分析】根据题意,设两种衬衣的原价都是x元,则甲衬衣的售价为60%x,乙衬衣的售价为70%x,列方程为:60%x+70%x=156,解方程即可。
【详解】解:设两种衬衣的原价都是x元,根据题意列方程如下:
60%x+70%x=156
1.3x=156
x=120
答:两种衬衣的原价是120元。
【点睛】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:甲种衬衣的现价+乙种衬衣的现价=156,进而列出方程是解答此类问题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
