1.1圆柱和圆锥的认识经典题型(同步练习)-小学数学六年级下册北师大版(含解析)
文档属性
| 名称 | 1.1圆柱和圆锥的认识经典题型(同步练习)-小学数学六年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 21:23:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.1圆柱和圆锥的认识经典题型(同步练习)
一、选择题
1.制作一个无盖的水桶,以下哪种铁皮可供搭配?应选择( )。
A.①和④ B.②和③ C.①和③
2.用丝带捆扎一种圆柱形礼品盒,打结处为20厘米。捆扎这种礼品盒用长为( )厘米的丝带比较合适。
A.22分米 B.240厘米 C.19.5分米 D.22.5分米
3.圆柱有( )条高,圆锥有( )条高。
①1 ②2 ③3 ④无数
A.①② B.①③ C.②③ D.④①
4.把一个棱长是8dm的正方体削成一个最大的圆柱,这个圆柱的底面半径是( )。
A.8dm B.25.12dm C.12.56dm D.4dm
5.下列物体中,由正方形绕一条边旋转形成的物体是( ).
A. B. C. D.
6.把一个圆锥沿底面直径到顶点切开,切面是一个( )。
A.圆形 B.三角形 C.扇形 D.无法确定
二、填空题
7.圆锥有( )个顶点、( )个底面和( )个侧面,它的底面是一个( )。
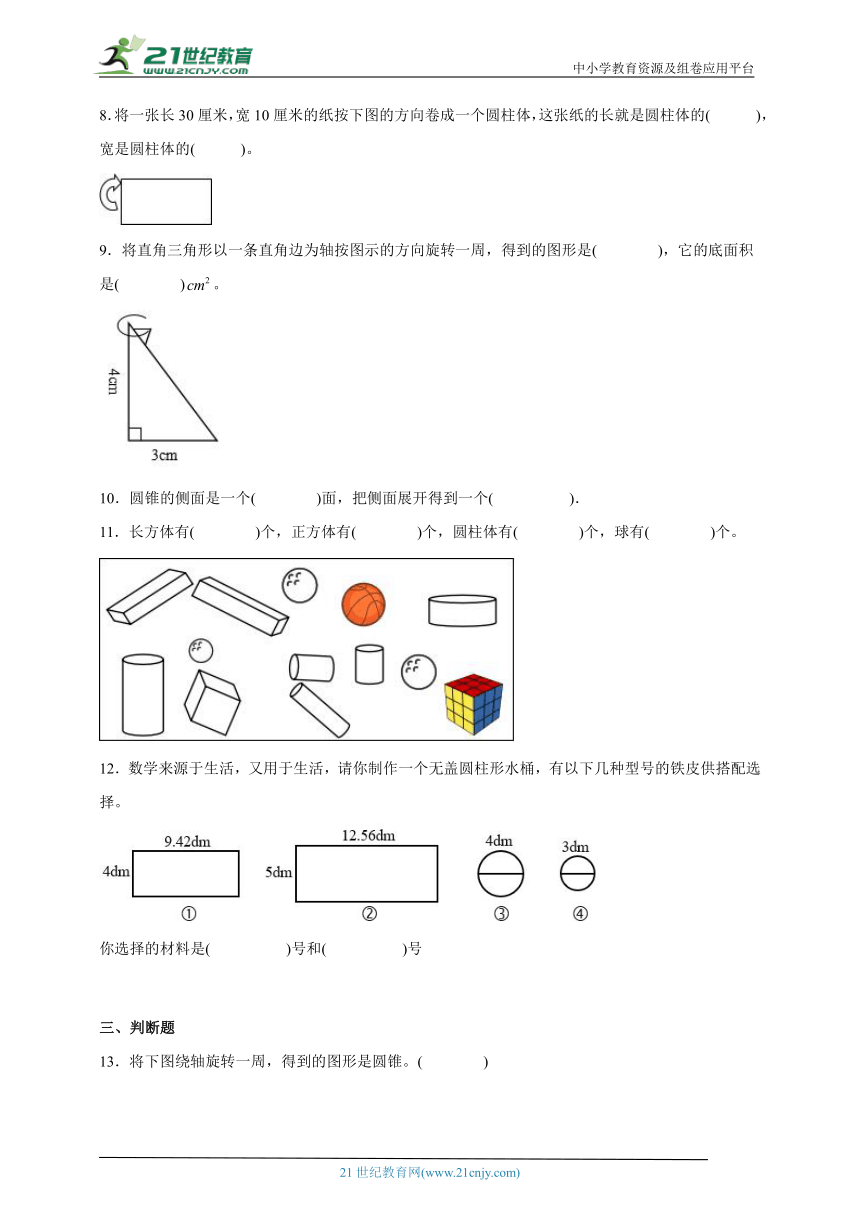
8.将一张长30厘米,宽10厘米的纸按下图的方向卷成一个圆柱体,这张纸的长就是圆柱体的( ),宽是圆柱体的( )。
9.将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是( ),它的底面积是( )。
10.圆锥的侧面是一个( )面,把侧面展开得到一个( ).
11.长方体有( )个,正方体有( )个,圆柱体有( )个,球有( )个。
12.数学来源于生活,又用于生活,请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的材料是( )号和( )号
三、判断题
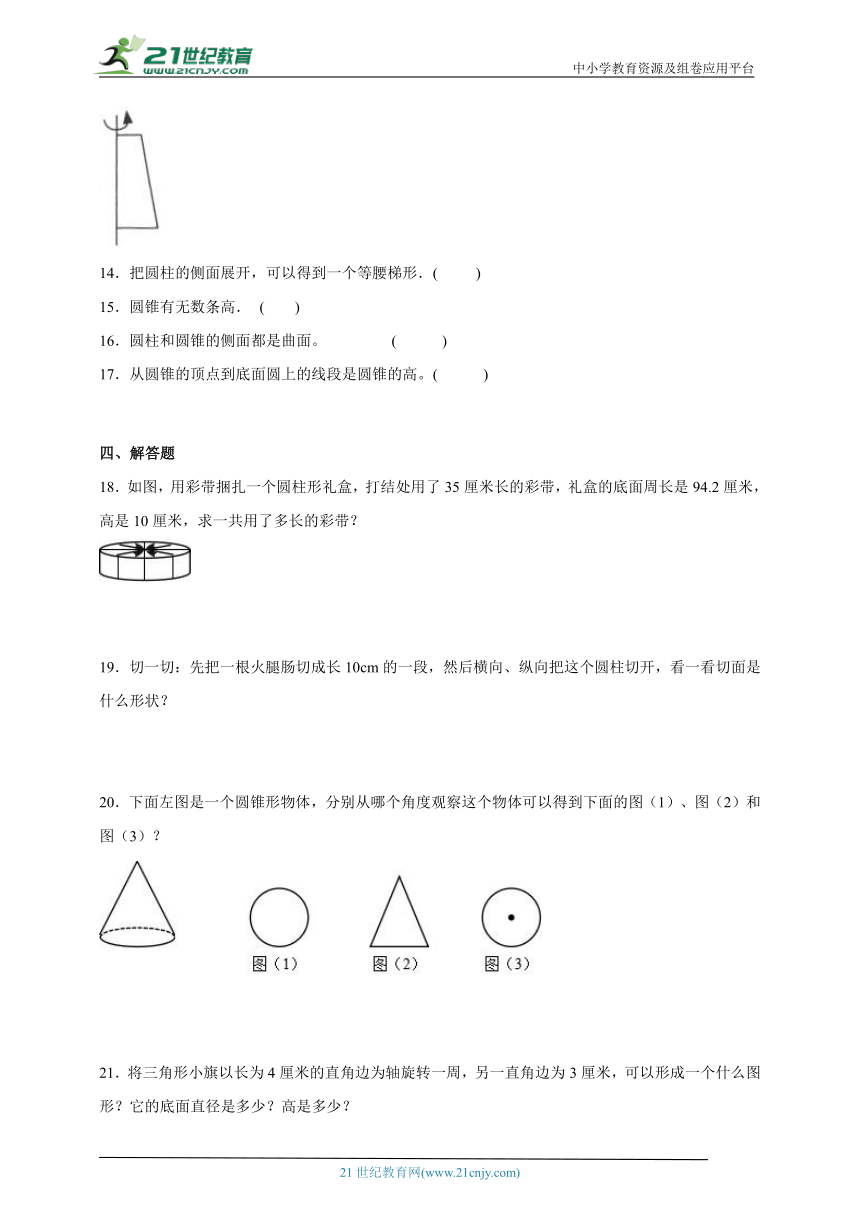
13.将下图绕轴旋转一周,得到的图形是圆锥。( )
14.把圆柱的侧面展开,可以得到一个等腰梯形.( )
15.圆锥有无数条高. ( )
16.圆柱和圆锥的侧面都是曲面。 ( )
17.从圆锥的顶点到底面圆上的线段是圆锥的高。( )
四、解答题
18.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
19.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
20.下面左图是一个圆锥形物体,分别从哪个角度观察这个物体可以得到下面的图(1)、图(2)和图(3)?
21.将三角形小旗以长为4厘米的直角边为轴旋转一周,另一直角边为3厘米,可以形成一个什么图形?它的底面直径是多少?高是多少?
22.把一个直径为20分米的圆形铁皮剪下一半围成一个圆锥,该圆锥的用铁皮多少平方分米?该圆锥的底面圆半径是多少分米?(接头不计,π取两位小数)
参考答案:
1.B
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出直径是3cm和半径是4cm的圆的周长,再进行比较,圆的周长与长方形的长相等,即可搭配成圆柱形水桶,据此解答。
【详解】直径3cm圆的周长:
3.14×3=9.42(cm)
半径4cm的圆的周长:
3.14×4×2
=12.56×2
=25.12(cm)
9.42=9.42
②和③可以搭配。
故答案为:B
【点睛】利用圆柱的特征以及圆的周长公式进行解答。
2.B
【分析】通过观察,捆扎这个盒子至少用去丝带长度为4个礼品盒底面直径和4个礼品盒高,再加上打结用去绳长的20厘米,由此得解。
【详解】30×4+25×4+20
=120+100+20
=240(厘米)
捆扎这种礼品盒用长为240厘米的丝带比较合适。
故答案为:B
【点睛】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带。
3.D
【解析】圆柱的高是两个底面之间的距离,一个圆柱有无数条高;
圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高。
【详解】根据分析可知,圆柱有无数条高,圆锥有1条高。
故答案为:D
【点睛】学生应该熟练掌握圆柱的高和圆锥的高。
4.D
【解析】把一个棱长是8dm的正方体削成一个最大的圆柱,这个圆柱的底面直径是正方体的棱长,直径÷2即可求出半径。
【详解】8÷2=4(dm)
故答案为:D
【点睛】分析出圆柱的底面直径是正方体的棱长,是解决此题的关键。
5.C
【解析】回答此类问题,可以通过观察旋转后图形的一半得到答案.
【详解】A选项的一半是半圆,故是由半圆旋转而得;B选项的一半是长方形,故是由长方形旋转而得;C选项的一半是正方形,故由正方形旋转而得;D选项的一半是直角三角形,故由直角三角形旋转而得.
6.B
【详解】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形。
故选:B
7. 1(或一) 1(或一) 1(或一) 圆形(或圆)
【详解】圆锥有1个顶点、1个底面和1个侧面,它的底面是一个圆形。
8. 底面周长 高
【分析】圆柱可以由长方形卷曲而得到
两种方式:
1.以长方形的长为底面周长,宽为高;
2.以长方形的宽为底面周长,长为高
【详解】根据分析可知,这张纸的长就是圆柱体的底面周长,宽是圆柱体的高。
故答案为:底面周长;高
【点睛】圆柱形成的另外一种方式:以长方形的一边为轴旋转而得到。
9. 圆锥 28.26
【分析】由题意知:将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是一个圆锥。底面是一个半径为3厘米的圆,用圆的面积公式计算即可得底面积。
【详解】如图,
将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是圆锥;
。
【点睛】掌握圆锥的特征是解答本题的关键。
10. 曲 扇形
【详解】略
11. 2 2 5 4
【分析】根据立体图形的特点,数清楚图片上各种图形的数量,即可得出答案。
【详解】从图上可得:长方体有2个,正方体有2个,圆柱体有5个,球有4个。
【点睛】本题考查学生对立体图形特点的掌握和运用。
12. ② ③
【分析】根据圆柱的特点,圆柱的底面周长等于侧面展开图长方形的长,据此进行选择即可。
【详解】3.14×4=12.56(dm)
则应选择的材料是②号和③号
【点睛】本题考查圆柱,明确圆柱的特征是解题的关键。
13.×
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360°而成的曲面所围成的几何体叫做圆锥,据此解答。
【详解】将绕轴旋转一周,得到的图形是不是圆锥,圆锥体应该是。
故答案为:×
【点睛】掌握圆锥的特征是解答题目的关键。
14.错误
【详解】因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,
所以,将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形;
无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
故答案为错误.
【分析】因为圆柱是由上下两个完全一样的圆面和一个侧面组成的图形,因此无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
15.×
【详解】圆锥只有一条高,圆锥的高是圆锥的顶点到底面圆心的距离,两点确定一条线段,因此圆锥只有一条高.
故答案为错误.
16.√
【分析】根据圆柱和圆锥的特征即可解答。
【详解】圆柱和圆锥都是由长方形和直角三角形沿直角边旋转得到的,所以它们的侧面都是曲面。
所以原题说法正确。
【点睛】此题主要考查了圆柱和圆锥的特征,圆柱和圆锥的侧面都是一个曲面。
17.×
【分析】根据圆锥的高:圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。以此判断。
【详解】从圆锥的顶点到底面圆上的线段是圆锥的高,并没有说明是到圆心最短的距离。
所以原题说法错误。
【点睛】此题主要考查学生对圆锥高定义的理解。
18.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点睛】本题考查了圆柱的特征,用圆柱的底面周长÷π=底面直径。
19.圆,长方形(或正方形)。
.
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
20.从底面观察,可以得到图(1);
从正面或侧面观察,可以得到图(2);
从上面观察,可以得到图(3)。
【详解】一个圆锥,从上面看是一个圆形,可以看到圆心,从侧面或是正面看到的是一个三角形,从底面看是一个圆形,看不到圆心。
21.圆锥;6厘米;4厘米
【详解】底面半径:3厘米
底面直径:3×2=6(厘米)
答:直角三角形小旗以4厘米为轴旋转,可以形成一个圆锥,它的底面直径是6厘米,高是4厘米。
22.15.7平方分米;62.8分米
【分析】通过分析,先求得半圆面积,就是圆锥侧面积;根据圆周长的一半为圆锥底面圆的周长再求圆锥底面圆的半径.
【详解】() π÷2=15.7(平方分米) 20π÷2÷2π=5(分米)
答:用铁皮15.7平方分米;底面圆半径是5分米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1圆柱和圆锥的认识经典题型(同步练习)
一、选择题
1.制作一个无盖的水桶,以下哪种铁皮可供搭配?应选择( )。
A.①和④ B.②和③ C.①和③
2.用丝带捆扎一种圆柱形礼品盒,打结处为20厘米。捆扎这种礼品盒用长为( )厘米的丝带比较合适。
A.22分米 B.240厘米 C.19.5分米 D.22.5分米
3.圆柱有( )条高,圆锥有( )条高。
①1 ②2 ③3 ④无数
A.①② B.①③ C.②③ D.④①
4.把一个棱长是8dm的正方体削成一个最大的圆柱,这个圆柱的底面半径是( )。
A.8dm B.25.12dm C.12.56dm D.4dm
5.下列物体中,由正方形绕一条边旋转形成的物体是( ).
A. B. C. D.
6.把一个圆锥沿底面直径到顶点切开,切面是一个( )。
A.圆形 B.三角形 C.扇形 D.无法确定
二、填空题
7.圆锥有( )个顶点、( )个底面和( )个侧面,它的底面是一个( )。
8.将一张长30厘米,宽10厘米的纸按下图的方向卷成一个圆柱体,这张纸的长就是圆柱体的( ),宽是圆柱体的( )。
9.将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是( ),它的底面积是( )。
10.圆锥的侧面是一个( )面,把侧面展开得到一个( ).
11.长方体有( )个,正方体有( )个,圆柱体有( )个,球有( )个。
12.数学来源于生活,又用于生活,请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮供搭配选择。
你选择的材料是( )号和( )号
三、判断题
13.将下图绕轴旋转一周,得到的图形是圆锥。( )
14.把圆柱的侧面展开,可以得到一个等腰梯形.( )
15.圆锥有无数条高. ( )
16.圆柱和圆锥的侧面都是曲面。 ( )
17.从圆锥的顶点到底面圆上的线段是圆锥的高。( )
四、解答题
18.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?
19.切一切:先把一根火腿肠切成长10cm的一段,然后横向、纵向把这个圆柱切开,看一看切面是什么形状?
20.下面左图是一个圆锥形物体,分别从哪个角度观察这个物体可以得到下面的图(1)、图(2)和图(3)?
21.将三角形小旗以长为4厘米的直角边为轴旋转一周,另一直角边为3厘米,可以形成一个什么图形?它的底面直径是多少?高是多少?
22.把一个直径为20分米的圆形铁皮剪下一半围成一个圆锥,该圆锥的用铁皮多少平方分米?该圆锥的底面圆半径是多少分米?(接头不计,π取两位小数)
参考答案:
1.B
【分析】根据圆的周长公式:周长=π×半径×2,代入数据,求出直径是3cm和半径是4cm的圆的周长,再进行比较,圆的周长与长方形的长相等,即可搭配成圆柱形水桶,据此解答。
【详解】直径3cm圆的周长:
3.14×3=9.42(cm)
半径4cm的圆的周长:
3.14×4×2
=12.56×2
=25.12(cm)
9.42=9.42
②和③可以搭配。
故答案为:B
【点睛】利用圆柱的特征以及圆的周长公式进行解答。
2.B
【分析】通过观察,捆扎这个盒子至少用去丝带长度为4个礼品盒底面直径和4个礼品盒高,再加上打结用去绳长的20厘米,由此得解。
【详解】30×4+25×4+20
=120+100+20
=240(厘米)
捆扎这种礼品盒用长为240厘米的丝带比较合适。
故答案为:B
【点睛】此题要求学生要有空间想象力,能够想到底面和背面也有和我们现在看到的一样多的丝带。
3.D
【解析】圆柱的高是两个底面之间的距离,一个圆柱有无数条高;
圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高。
【详解】根据分析可知,圆柱有无数条高,圆锥有1条高。
故答案为:D
【点睛】学生应该熟练掌握圆柱的高和圆锥的高。
4.D
【解析】把一个棱长是8dm的正方体削成一个最大的圆柱,这个圆柱的底面直径是正方体的棱长,直径÷2即可求出半径。
【详解】8÷2=4(dm)
故答案为:D
【点睛】分析出圆柱的底面直径是正方体的棱长,是解决此题的关键。
5.C
【解析】回答此类问题,可以通过观察旋转后图形的一半得到答案.
【详解】A选项的一半是半圆,故是由半圆旋转而得;B选项的一半是长方形,故是由长方形旋转而得;C选项的一半是正方形,故由正方形旋转而得;D选项的一半是直角三角形,故由直角三角形旋转而得.
6.B
【详解】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形。
故选:B
7. 1(或一) 1(或一) 1(或一) 圆形(或圆)
【详解】圆锥有1个顶点、1个底面和1个侧面,它的底面是一个圆形。
8. 底面周长 高
【分析】圆柱可以由长方形卷曲而得到
两种方式:
1.以长方形的长为底面周长,宽为高;
2.以长方形的宽为底面周长,长为高
【详解】根据分析可知,这张纸的长就是圆柱体的底面周长,宽是圆柱体的高。
故答案为:底面周长;高
【点睛】圆柱形成的另外一种方式:以长方形的一边为轴旋转而得到。
9. 圆锥 28.26
【分析】由题意知:将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是一个圆锥。底面是一个半径为3厘米的圆,用圆的面积公式计算即可得底面积。
【详解】如图,
将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是圆锥;
。
【点睛】掌握圆锥的特征是解答本题的关键。
10. 曲 扇形
【详解】略
11. 2 2 5 4
【分析】根据立体图形的特点,数清楚图片上各种图形的数量,即可得出答案。
【详解】从图上可得:长方体有2个,正方体有2个,圆柱体有5个,球有4个。
【点睛】本题考查学生对立体图形特点的掌握和运用。
12. ② ③
【分析】根据圆柱的特点,圆柱的底面周长等于侧面展开图长方形的长,据此进行选择即可。
【详解】3.14×4=12.56(dm)
则应选择的材料是②号和③号
【点睛】本题考查圆柱,明确圆柱的特征是解题的关键。
13.×
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360°而成的曲面所围成的几何体叫做圆锥,据此解答。
【详解】将绕轴旋转一周,得到的图形是不是圆锥,圆锥体应该是。
故答案为:×
【点睛】掌握圆锥的特征是解答题目的关键。
14.错误
【详解】因为把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;
当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;
当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,
所以,将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形;
无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
故答案为错误.
【分析】因为圆柱是由上下两个完全一样的圆面和一个侧面组成的图形,因此无论如何将圆柱的侧面展开都不会得到一个等腰梯形.
15.×
【详解】圆锥只有一条高,圆锥的高是圆锥的顶点到底面圆心的距离,两点确定一条线段,因此圆锥只有一条高.
故答案为错误.
16.√
【分析】根据圆柱和圆锥的特征即可解答。
【详解】圆柱和圆锥都是由长方形和直角三角形沿直角边旋转得到的,所以它们的侧面都是曲面。
所以原题说法正确。
【点睛】此题主要考查了圆柱和圆锥的特征,圆柱和圆锥的侧面都是一个曲面。
17.×
【分析】根据圆锥的高:圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。以此判断。
【详解】从圆锥的顶点到底面圆上的线段是圆锥的高,并没有说明是到圆心最短的距离。
所以原题说法错误。
【点睛】此题主要考查学生对圆锥高定义的理解。
18.355厘米
【分析】根据题意可知,先求出这个圆柱的底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答。
【详解】94.2÷3.14×8+10×8+35
=240+80+35
=355(厘米)
答:一共用了355厘米的彩带。
【点睛】本题考查了圆柱的特征,用圆柱的底面周长÷π=底面直径。
19.圆,长方形(或正方形)。
.
【详解】横向切开是平行于底面切开的,切开后切面是圆形;纵向切开是平行于高切开的,切开后切面是长方形(或正方形).
20.从底面观察,可以得到图(1);
从正面或侧面观察,可以得到图(2);
从上面观察,可以得到图(3)。
【详解】一个圆锥,从上面看是一个圆形,可以看到圆心,从侧面或是正面看到的是一个三角形,从底面看是一个圆形,看不到圆心。
21.圆锥;6厘米;4厘米
【详解】底面半径:3厘米
底面直径:3×2=6(厘米)
答:直角三角形小旗以4厘米为轴旋转,可以形成一个圆锥,它的底面直径是6厘米,高是4厘米。
22.15.7平方分米;62.8分米
【分析】通过分析,先求得半圆面积,就是圆锥侧面积;根据圆周长的一半为圆锥底面圆的周长再求圆锥底面圆的半径.
【详解】() π÷2=15.7(平方分米) 20π÷2÷2π=5(分米)
答:用铁皮15.7平方分米;底面圆半径是5分米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
