【班海精品】北师大(新)版 四下 数学好玩 1.密铺【优质课件】
文档属性
| 名称 | 【班海精品】北师大(新)版 四下 数学好玩 1.密铺【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:21:08 | ||
图片预览






文档简介
(共20张PPT)
密铺
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
课前导入
新课精讲
学以致用
课堂小结
01
课前导入
情景导入
三角形能不能密铺?四边形可不可以?
02
新课精讲
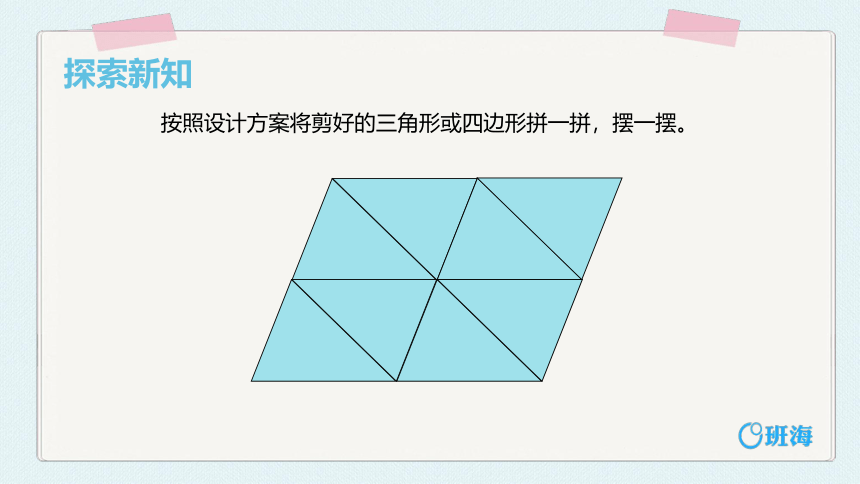
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
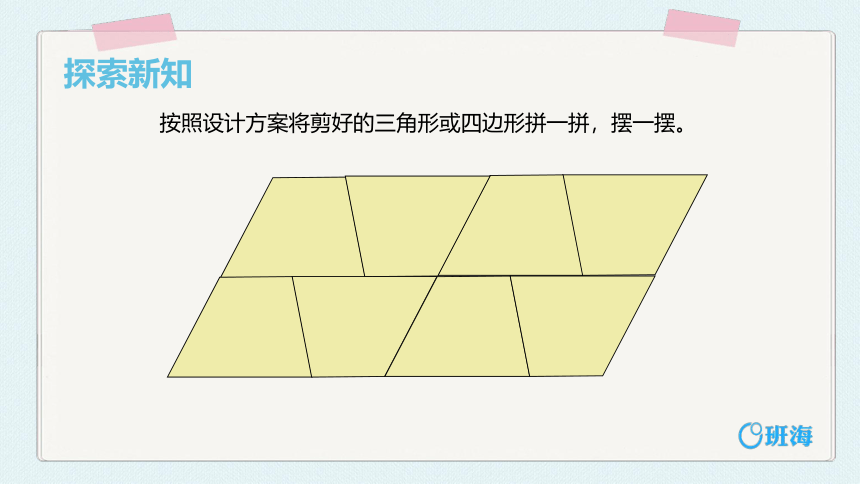
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
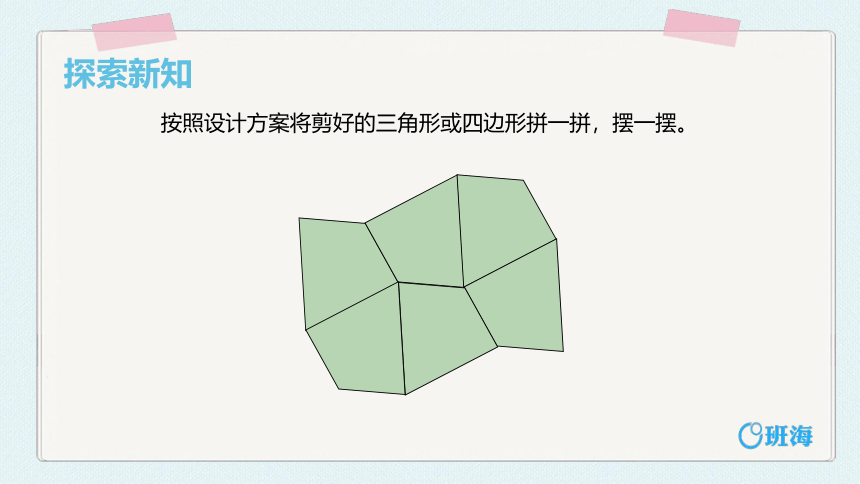
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
探索新知
全班交流密铺的作品,三角形能不能密铺?四边形呢?
观察发现:图形之间都没有空隙,也不重叠,根据密铺的意义可知,三角形和四边形都可以密铺。
探索新知
请按照下面的方法试一试,你有什么发现?
探索新知
在上面的活动中,你有什么收获?还有哪些想要进一步
研究的问题?
典题精讲
1.看一看,想一想,填一填。(同一图形中相等的角所标记号
相同)
(1)图1是相同的四边形,拼接处正好是它的四个角,四边形的内角和正好是( )°。
(2)图2是相同的三角形,拼接处三角形的每个角正好用( )次。三角形内角和是( )°,所以( )个( )°正好是( )°。
360
2
180
180
2
360
典题精讲
2.拼一拼,看一看,填一填。
(1)这是正五边形,( )(填“能”或“不能”)密铺。正五
边形每个内角是108°,108°×3=324°,拼接处不是( )°。
(2)密铺与图形的角有关系。只要图形的内角能合成( )°,就可以密铺。
不能
360
360
易错提醒
判断。(对的画“√”,错的画“×”)
(1)只要图形之间没有空隙,就是密铺。 ( )
(2)所有的平面图形都能密铺。 ( )
(3)密铺时只能用一种图形。 ( )
(4)任意形状、大小相同的三角形都能密铺。 ( )
×
辨析:能够密铺的图形拼接处既不能有空隙,也不能重叠。
×
辨析:当围绕一点拼在一起的n 个多边形的内角加在一起
恰好是360°时,能密铺。不是所有的平面图形都能密铺。
×
√
辨析:密铺可以用一种或几种图形。
03
学以致用
小试牛刀
1.不是所有的平面图形都可以密铺。看一看,试一试。
由正五边形的内角和
=(5-2)×180°=540°,
得每个角的度数是540°÷5=108°,108°×3=324°,
324°<360°,所以正五边形不能密铺。
由正六边形的内角和
=(6-2)×180°=720°,
得每个角的度数是720°÷6=120°120°×3=360°,
所以正六边形能密铺。
小试牛刀
2.看一看下面的密铺图案,想一想它们是如何形成的。
第四幅图是由不规则图形密铺成的图案。
第一幅图是由四边形密铺成的图案
第二幅图是由正六边形密铺成的图案
第三幅图是由不规则图形密铺成的图案
04
课堂小结
归纳总结:
当围绕一点拼在一起的几个多边形的内角加在一起恰好是360°时,能密铺成一个平面图形。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
密铺
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
课前导入
新课精讲
学以致用
课堂小结
01
课前导入
情景导入
三角形能不能密铺?四边形可不可以?
02
新课精讲
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
探索新知
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
探索新知
全班交流密铺的作品,三角形能不能密铺?四边形呢?
观察发现:图形之间都没有空隙,也不重叠,根据密铺的意义可知,三角形和四边形都可以密铺。
探索新知
请按照下面的方法试一试,你有什么发现?
探索新知
在上面的活动中,你有什么收获?还有哪些想要进一步
研究的问题?
典题精讲
1.看一看,想一想,填一填。(同一图形中相等的角所标记号
相同)
(1)图1是相同的四边形,拼接处正好是它的四个角,四边形的内角和正好是( )°。
(2)图2是相同的三角形,拼接处三角形的每个角正好用( )次。三角形内角和是( )°,所以( )个( )°正好是( )°。
360
2
180
180
2
360
典题精讲
2.拼一拼,看一看,填一填。
(1)这是正五边形,( )(填“能”或“不能”)密铺。正五
边形每个内角是108°,108°×3=324°,拼接处不是( )°。
(2)密铺与图形的角有关系。只要图形的内角能合成( )°,就可以密铺。
不能
360
360
易错提醒
判断。(对的画“√”,错的画“×”)
(1)只要图形之间没有空隙,就是密铺。 ( )
(2)所有的平面图形都能密铺。 ( )
(3)密铺时只能用一种图形。 ( )
(4)任意形状、大小相同的三角形都能密铺。 ( )
×
辨析:能够密铺的图形拼接处既不能有空隙,也不能重叠。
×
辨析:当围绕一点拼在一起的n 个多边形的内角加在一起
恰好是360°时,能密铺。不是所有的平面图形都能密铺。
×
√
辨析:密铺可以用一种或几种图形。
03
学以致用
小试牛刀
1.不是所有的平面图形都可以密铺。看一看,试一试。
由正五边形的内角和
=(5-2)×180°=540°,
得每个角的度数是540°÷5=108°,108°×3=324°,
324°<360°,所以正五边形不能密铺。
由正六边形的内角和
=(6-2)×180°=720°,
得每个角的度数是720°÷6=120°120°×3=360°,
所以正六边形能密铺。
小试牛刀
2.看一看下面的密铺图案,想一想它们是如何形成的。
第四幅图是由不规则图形密铺成的图案。
第一幅图是由四边形密铺成的图案
第二幅图是由正六边形密铺成的图案
第三幅图是由不规则图形密铺成的图案
04
课堂小结
归纳总结:
当围绕一点拼在一起的几个多边形的内角加在一起恰好是360°时,能密铺成一个平面图形。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
