【班海精品】北师大(新)版五下 第四单元 3.长方体的体积【优质课件】
文档属性
| 名称 | 【班海精品】北师大(新)版五下 第四单元 3.长方体的体积【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:52 | ||
图片预览





文档简介
(共23张PPT)
长方体的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课 前 导 入
情景导入
物体所占空间的大小叫做物体的( )。
体积
计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( ) 。
立方厘米
立方分米
立方米
cm3
dm3
m3
同学们,刚刚的知识点内容填空,你都答对了吗?
02
新 课 精 讲
探索新知
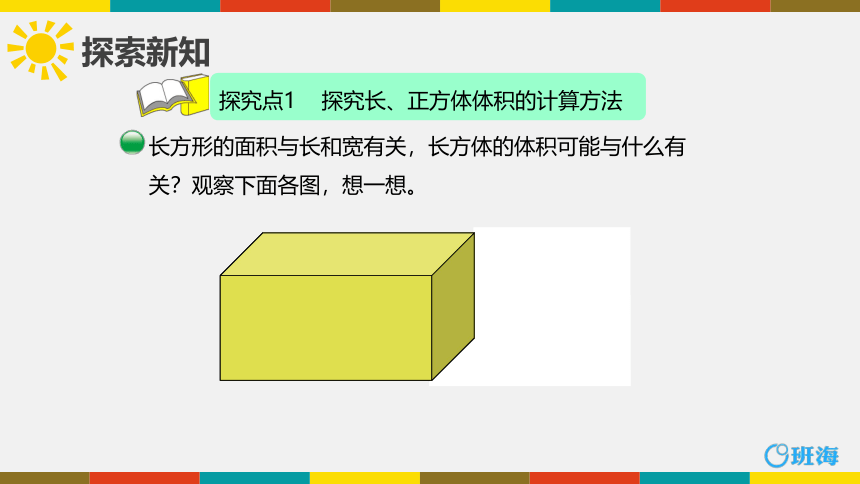
长方形的面积与长和宽有关,长方体的体积可能与什么有关?观察下面各图,想一想。
探究点1 探究长、正方体体积的计算方法
探索新知
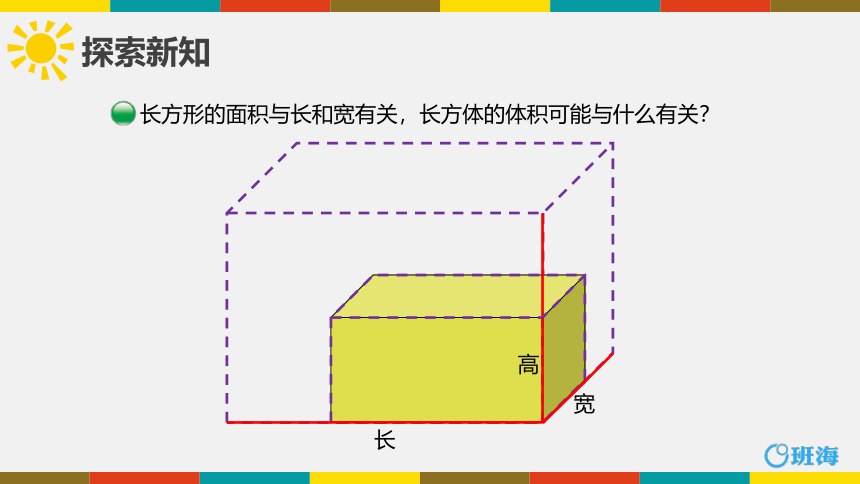
长方形的面积与长和宽有关,长方体的体积可能与什么有关?
高
宽
长
探索新知
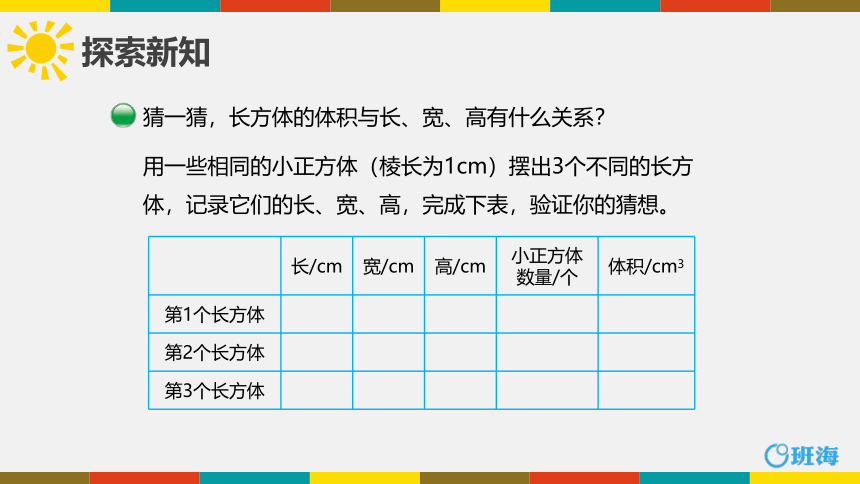
猜一猜,长方体的体积与长、宽、高有什么关系?
用一些相同的小正方体(棱长为1cm)摆出3个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
探索新知
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
长方体的体积= 长× 宽× 高
…
…
…
…
=
×
×
=
探索新知
如何计算正方体的体积?与同伴交流你的想法。
正方体的体积=棱长×棱长×棱长
=
×
×
=
典题精讲
1.数一数,填一填。
(1)右图是由棱长为1 cm的小正方体搭成的。这个长方体共用了( )个小正方体,所以长方体的体积是( )。
(2)通过观察发现:小正方体的总个数可以用长方体的( )×( )×( )迅速求出,所以推得长方体的体积=( )×( )×( ),用字母表示是( )。
36cm3
15
长
宽
高
长
宽
高
V=abh
典题精讲
2.选择。(将正确答案的字母填在括号里)
(1)长方体和正方体都可以用( )求出体积。
A.长×宽×高 B.棱长×棱长×棱长
C.底面积×高 D.棱长×12
(2)长方体的底面积扩大到原来的2倍,高也扩大到原来的2倍,体积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍
C.扩大到原来的8倍 D.不变
C
B
典题精讲
3.解决问题。
(1)一个长方体木箱,长是1.2 m,宽是0.8 m,高是0.5 m,这个木箱的体积是多少立方米?
(2)一个正方体粉笔盒的棱长是8 cm,这个粉笔盒的体积是多少立方厘米?
1.2×0.8×0.5=0.48(m3)
答:这个木箱的体积是0.48 m3。
8×8×8=512(cm3)
答:这个粉笔盒的体积是512 cm3。
易错提醒
1.一根方木横截面的面积是15 dm2,长是4 m,这根方木的体积是多少立方米?
辨析:计算体积时忽视了单位的统一。
15 dm2=0.15 m2
0.15×4=0.6(m3)
答:这根方木的体积是0.6 m3。
03
学 以 致 用
小试牛刀
1.一块长方体形状的大理石,体积为30m3,底面是面积为6m2的长方形,这块大理石的高多少米?
30÷6=5(m)
答:这块大理石的高5米。
2.一个长方体水池,底面长12dm,宽6dm。如果要向这个池子里注入2 dm高的水,需要多少升水?
12×6×2=144(dm3)=144(升)
答:需要144升水。
小试牛刀
3.牙膏盒长15 cm,宽和高都是3 cm。现有一纸箱,内侧的尺寸如图(单位:cm)。这个纸箱中最多能放多少盒牙膏?与同伴交流,说一说你是怎么想的。
60÷15=4
30÷3=10
4×10×10=400(盒)
答:这个纸箱中最多能放多少盒牙膏。
小试牛刀
4.将一个长8cm、宽5cm、高3cm的长方体截成一个 体积最大的正方体,这个正方体的体积是多少?结合下边的图想一想,再算一算。(单位:cm)
3×3×3=27(cm3)
答:这个正方体的体积是27 cm3
小试牛刀
5.冷藏车厢的内部长3m、宽2.2m、高2m,车厢内部的体积是多少?
3×2.2×2=13.2(m3)
答:车厢内部的体积是13.2 m3 。
小试牛刀
6.实践活动。
⑴寻找生活中两个长方体形状的物体,先估一估它们的体积,再进行测量与计算。
⑵设计一个长方体盒子,使它能装下1000块长方体橡皮。
04
课 堂 小 结
长方体(正方体)的体积= 底面积× 高,用公式表示为:V = Sh。
已知长方体的底面积、高、体积三个量中的任意两个量,可以求得第三个量。
归纳总结:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
长方体的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课 前 导 入
情景导入
物体所占空间的大小叫做物体的( )。
体积
计量体积要用体积单位,常用的体积单位有( )、( )和( ),可以分别写成( )、( )和( ) 。
立方厘米
立方分米
立方米
cm3
dm3
m3
同学们,刚刚的知识点内容填空,你都答对了吗?
02
新 课 精 讲
探索新知
长方形的面积与长和宽有关,长方体的体积可能与什么有关?观察下面各图,想一想。
探究点1 探究长、正方体体积的计算方法
探索新知
长方形的面积与长和宽有关,长方体的体积可能与什么有关?
高
宽
长
探索新知
猜一猜,长方体的体积与长、宽、高有什么关系?
用一些相同的小正方体(棱长为1cm)摆出3个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
探索新知
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
长方体的体积= 长× 宽× 高
…
…
…
…
=
×
×
=
探索新知
如何计算正方体的体积?与同伴交流你的想法。
正方体的体积=棱长×棱长×棱长
=
×
×
=
典题精讲
1.数一数,填一填。
(1)右图是由棱长为1 cm的小正方体搭成的。这个长方体共用了( )个小正方体,所以长方体的体积是( )。
(2)通过观察发现:小正方体的总个数可以用长方体的( )×( )×( )迅速求出,所以推得长方体的体积=( )×( )×( ),用字母表示是( )。
36cm3
15
长
宽
高
长
宽
高
V=abh
典题精讲
2.选择。(将正确答案的字母填在括号里)
(1)长方体和正方体都可以用( )求出体积。
A.长×宽×高 B.棱长×棱长×棱长
C.底面积×高 D.棱长×12
(2)长方体的底面积扩大到原来的2倍,高也扩大到原来的2倍,体积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍
C.扩大到原来的8倍 D.不变
C
B
典题精讲
3.解决问题。
(1)一个长方体木箱,长是1.2 m,宽是0.8 m,高是0.5 m,这个木箱的体积是多少立方米?
(2)一个正方体粉笔盒的棱长是8 cm,这个粉笔盒的体积是多少立方厘米?
1.2×0.8×0.5=0.48(m3)
答:这个木箱的体积是0.48 m3。
8×8×8=512(cm3)
答:这个粉笔盒的体积是512 cm3。
易错提醒
1.一根方木横截面的面积是15 dm2,长是4 m,这根方木的体积是多少立方米?
辨析:计算体积时忽视了单位的统一。
15 dm2=0.15 m2
0.15×4=0.6(m3)
答:这根方木的体积是0.6 m3。
03
学 以 致 用
小试牛刀
1.一块长方体形状的大理石,体积为30m3,底面是面积为6m2的长方形,这块大理石的高多少米?
30÷6=5(m)
答:这块大理石的高5米。
2.一个长方体水池,底面长12dm,宽6dm。如果要向这个池子里注入2 dm高的水,需要多少升水?
12×6×2=144(dm3)=144(升)
答:需要144升水。
小试牛刀
3.牙膏盒长15 cm,宽和高都是3 cm。现有一纸箱,内侧的尺寸如图(单位:cm)。这个纸箱中最多能放多少盒牙膏?与同伴交流,说一说你是怎么想的。
60÷15=4
30÷3=10
4×10×10=400(盒)
答:这个纸箱中最多能放多少盒牙膏。
小试牛刀
4.将一个长8cm、宽5cm、高3cm的长方体截成一个 体积最大的正方体,这个正方体的体积是多少?结合下边的图想一想,再算一算。(单位:cm)
3×3×3=27(cm3)
答:这个正方体的体积是27 cm3
小试牛刀
5.冷藏车厢的内部长3m、宽2.2m、高2m,车厢内部的体积是多少?
3×2.2×2=13.2(m3)
答:车厢内部的体积是13.2 m3 。
小试牛刀
6.实践活动。
⑴寻找生活中两个长方体形状的物体,先估一估它们的体积,再进行测量与计算。
⑵设计一个长方体盒子,使它能装下1000块长方体橡皮。
04
课 堂 小 结
长方体(正方体)的体积= 底面积× 高,用公式表示为:V = Sh。
已知长方体的底面积、高、体积三个量中的任意两个量,可以求得第三个量。
归纳总结:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
