【核心素养目标】24.2.3圆心角、弧、弦、弦心距之间的关系 教学设计
文档属性
| 名称 | 【核心素养目标】24.2.3圆心角、弧、弦、弦心距之间的关系 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 17:30:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数24.2.3圆心角、弧、弦、弦心距之间的关系教学设计
课题 24.2.3圆心角、弧、弦、弦心距之间的关系 单元 第24单元 学科 数学 年级 九
教材分析 本节主要学习,在同圆或等圆中,两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距,它们之间的相等关系,圆心角与下一节学习的圆周角有一定关系,起到承上启下的作用,本节利用相等关系证明几何问题,计算相关的角和线段。
核心素养分析 本节探究学习了,在同圆或等圆中,两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距,它们之间有一组量相等,其余都相等,培养了几何直观的核心素养,锻炼了学生的计算能力。
学习目标 1.理解圆是旋转对称图形;2.掌握圆心角与所对的弦、所对弦的弦心距的关系:同圆或等圆中,两个圆心角、两条弧和两条弦、弦心距中,有一组量相等,则对应的其余各组量分别相等;3. 能够运用定理,证明几何结论,求圆中的角和线段。
重点 握圆心角与所对的弦、所对弦的弦心距的关系:同圆或等圆中,两个圆心角、两条弧和两条弦、弦心距中,有一组量相等,则对应的其余各组量分别相等
难点 能够运用定理,证明几何结论,求圆中的角和线段
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )A.①② ③④ B.①③ ②④ C.①④ ②③ D.②③ ①④解:垂直于弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直于弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B. 学生观察图片,学生回答,找其他学生进行补充,以培养学生温顾知识,大胆发言的良好习惯。 由平移、轴对称等图形变换本节课,导入图形的旋转,进行知识的迁移。
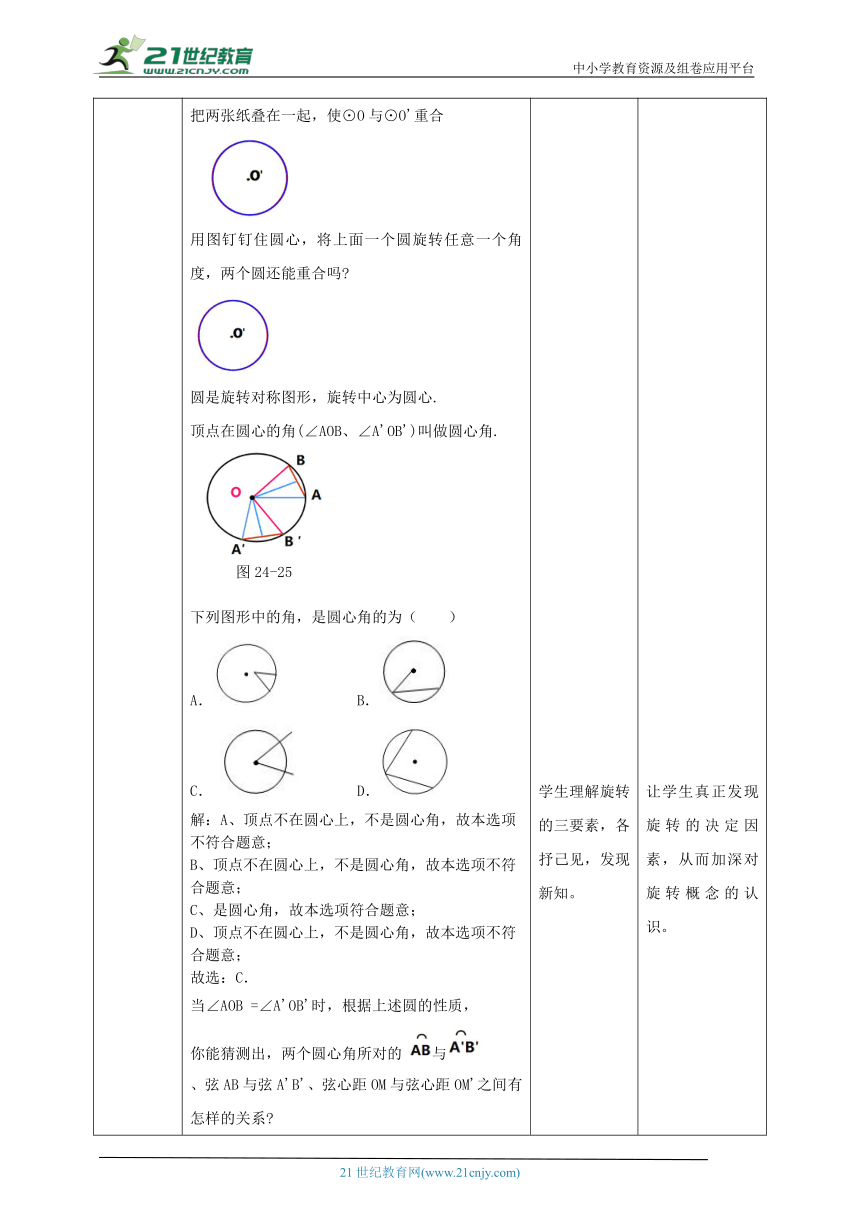
讲授新课 我们已经知道,圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线,那么圆是中心对称图形吗 在两张透明纸上,分别作半径相等的⊙O和⊙O'把两张纸叠在一起,使⊙O与⊙O'重合用图钉钉住圆心,将上面一个圆旋转任意一个角度,两个圆还能重合吗 圆是旋转对称图形,旋转中心为圆心.顶点在圆心的角(∠AOB、∠A'OB')叫做圆心角.图24-25下列图形中的角,是圆心角的为( )A. B. C. D.解:A、顶点不在圆心上,不是圆心角,故本选项不符合题意;B、顶点不在圆心上,不是圆心角,故本选项不符合题意;C、是圆心角,故本选项符合题意;D、顶点不在圆心上,不是圆心角,故本选项不符合题意;故选:C.当∠AOB =∠A'OB'时,根据上述圆的性质,你能猜测出,两个圆心角所对的 与、弦AB与弦A'B'、弦心距OM与弦心距OM'之间有怎样的关系 思考根据圆的旋转对称性,把∠AOB连同绕圆心О旋转,使线段OA与OA'重合,设∠A'OA =α.∠AOB=∠A'OB' ,∠B'OB=∠A'OB'+∠A'OB=∠AOB+∠A'OB =α.线段OB与线段OB'重合.又OA =OA' ,OB =OB',旋转后点A与点A'重合,点B与点B'重合。这样,弧AB与弧A'B'重合,弦AB与弦A'B'重合,弦心距OM与弦心距OM'也重合,即弧AB =弧A'B' ,AB =A'B' ,OM =OM'.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等。在同圆或等圆中,圆心角相等 弧相等 弦相等 弦心距相等.在同心圆中,若圆心角∠BOC=∠AOC相等,可以得到AB=A'B' OC=O'C' 吗? 不能 把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角。因为同圆中相等的圆心角所对的弧相等,所以整个圆周也被等分成360份,我们把每一份这样的弧叫做1°的弧。 一般地,n°的圆心角对着n的弧,n°的弧对着n°的圆心角.也就是说,圆心角的度数和它所对的弧的度数相等.例4 已知:如图24-26,等边三角形ABC的三个顶点都在⊙O上.求证:∠AOB=∠BOC=∠COA =120°.证明 连接OA,OB, OC.∵AB=BC=CA,∴∠AOB = ∠BOC =∠COA=×360°=120°.图24-26例5 已知:如图24-27 ,点O是∠A平分线上的一点,⊙O分别交∠A两边于点C,D和点E,F.求证:CD=EF.证明 过点O作 OK⊥CD、OK'⊥EF ,垂足分别为K,K'.∵OK =OK'(角平分线性质),∴CD=EF.图24-27 图24-28例6 如图24-28,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE//AB,为40°,求∠BOD的度数.解 连接OE.∵弧CE为40°,∴∠COE =40°.∵OC= OE, ∴∠C= ∵CE//AB,∴∠AOD =∠C= 70°.∴∠BOD = 180°-70°=110°.在同圆或等圆中,圆心角相等 弧相等 弦相等 弦心距相等 学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。学生理解旋转的三要素,各抒己见,发现新知。 学生理解旋转的性质以及旋转对称图形的概念。 通过生活中的实际例子,帮助学生理解旋转的定义。让学生真正发现旋转的决定因素,从而加深对旋转概念的认识。 认识规律,并用旋转的性质解题。
课堂练习 下面四个图中的角,是圆心角的是( )A. B.
C. D. 解:根据圆心角的定义,圆心角是顶点在圆心,角的两边与圆相交的角。故选D.2.如图,在同圆中,若∠AOC=2∠BOD,则AC____2BD.(填“>”“<”或“=”)解:如图,以OD为边作∠DOE=∠BOD,OE与⊙O交于点E,连接AC、BE、BD、ED,则∠BOE=2∠BOD,BD=DE,∵∠AOC=2∠BOD,∴∠AOC=∠BOE,∴AC=BE,在△BDE中,BE课堂小结 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等. 学生先发言总结本节旋转的性质,旋转对称图形概念,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.2.3圆心角、弧、弦、弦心距之间的关系1.圆是旋转对称图形2.弦、弧、弦心距、圆心角之间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数24.2.3圆心角、弧、弦、弦心距之间的关系教学设计
课题 24.2.3圆心角、弧、弦、弦心距之间的关系 单元 第24单元 学科 数学 年级 九
教材分析 本节主要学习,在同圆或等圆中,两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距,它们之间的相等关系,圆心角与下一节学习的圆周角有一定关系,起到承上启下的作用,本节利用相等关系证明几何问题,计算相关的角和线段。
核心素养分析 本节探究学习了,在同圆或等圆中,两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距,它们之间有一组量相等,其余都相等,培养了几何直观的核心素养,锻炼了学生的计算能力。
学习目标 1.理解圆是旋转对称图形;2.掌握圆心角与所对的弦、所对弦的弦心距的关系:同圆或等圆中,两个圆心角、两条弧和两条弦、弦心距中,有一组量相等,则对应的其余各组量分别相等;3. 能够运用定理,证明几何结论,求圆中的角和线段。
重点 握圆心角与所对的弦、所对弦的弦心距的关系:同圆或等圆中,两个圆心角、两条弧和两条弦、弦心距中,有一组量相等,则对应的其余各组量分别相等
难点 能够运用定理,证明几何结论,求圆中的角和线段
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )A.①② ③④ B.①③ ②④ C.①④ ②③ D.②③ ①④解:垂直于弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直于弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B. 学生观察图片,学生回答,找其他学生进行补充,以培养学生温顾知识,大胆发言的良好习惯。 由平移、轴对称等图形变换本节课,导入图形的旋转,进行知识的迁移。
讲授新课 我们已经知道,圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线,那么圆是中心对称图形吗 在两张透明纸上,分别作半径相等的⊙O和⊙O'把两张纸叠在一起,使⊙O与⊙O'重合用图钉钉住圆心,将上面一个圆旋转任意一个角度,两个圆还能重合吗 圆是旋转对称图形,旋转中心为圆心.顶点在圆心的角(∠AOB、∠A'OB')叫做圆心角.图24-25下列图形中的角,是圆心角的为( )A. B. C. D.解:A、顶点不在圆心上,不是圆心角,故本选项不符合题意;B、顶点不在圆心上,不是圆心角,故本选项不符合题意;C、是圆心角,故本选项符合题意;D、顶点不在圆心上,不是圆心角,故本选项不符合题意;故选:C.当∠AOB =∠A'OB'时,根据上述圆的性质,你能猜测出,两个圆心角所对的 与、弦AB与弦A'B'、弦心距OM与弦心距OM'之间有怎样的关系 思考根据圆的旋转对称性,把∠AOB连同绕圆心О旋转,使线段OA与OA'重合,设∠A'OA =α.∠AOB=∠A'OB' ,∠B'OB=∠A'OB'+∠A'OB=∠AOB+∠A'OB =α.线段OB与线段OB'重合.又OA =OA' ,OB =OB',旋转后点A与点A'重合,点B与点B'重合。这样,弧AB与弧A'B'重合,弦AB与弦A'B'重合,弦心距OM与弦心距OM'也重合,即弧AB =弧A'B' ,AB =A'B' ,OM =OM'.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角以及这两个角所对的弧、所对的弦、所对弦的弦心距中,有一组量相等,那么其余各组量都分别相等。在同圆或等圆中,圆心角相等 弧相等 弦相等 弦心距相等.在同心圆中,若圆心角∠BOC=∠AOC相等,可以得到AB=A'B' OC=O'C' 吗? 不能 把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角。因为同圆中相等的圆心角所对的弧相等,所以整个圆周也被等分成360份,我们把每一份这样的弧叫做1°的弧。 一般地,n°的圆心角对着n的弧,n°的弧对着n°的圆心角.也就是说,圆心角的度数和它所对的弧的度数相等.例4 已知:如图24-26,等边三角形ABC的三个顶点都在⊙O上.求证:∠AOB=∠BOC=∠COA =120°.证明 连接OA,OB, OC.∵AB=BC=CA,∴∠AOB = ∠BOC =∠COA=×360°=120°.图24-26例5 已知:如图24-27 ,点O是∠A平分线上的一点,⊙O分别交∠A两边于点C,D和点E,F.求证:CD=EF.证明 过点O作 OK⊥CD、OK'⊥EF ,垂足分别为K,K'.∵OK =OK'(角平分线性质),∴CD=EF.图24-27 图24-28例6 如图24-28,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE//AB,为40°,求∠BOD的度数.解 连接OE.∵弧CE为40°,∴∠COE =40°.∵OC= OE, ∴∠C= ∵CE//AB,∴∠AOD =∠C= 70°.∴∠BOD = 180°-70°=110°.在同圆或等圆中,圆心角相等 弧相等 弦相等 弦心距相等 学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。学生理解旋转的三要素,各抒己见,发现新知。 学生理解旋转的性质以及旋转对称图形的概念。 通过生活中的实际例子,帮助学生理解旋转的定义。让学生真正发现旋转的决定因素,从而加深对旋转概念的认识。 认识规律,并用旋转的性质解题。
课堂练习 下面四个图中的角,是圆心角的是( )A. B.
C. D. 解:根据圆心角的定义,圆心角是顶点在圆心,角的两边与圆相交的角。故选D.2.如图,在同圆中,若∠AOC=2∠BOD,则AC____2BD.(填“>”“<”或“=”)解:如图,以OD为边作∠DOE=∠BOD,OE与⊙O交于点E,连接AC、BE、BD、ED,则∠BOE=2∠BOD,BD=DE,∵∠AOC=2∠BOD,∴∠AOC=∠BOE,∴AC=BE,在△BDE中,BE
板书 课题:24.2.3圆心角、弧、弦、弦心距之间的关系1.圆是旋转对称图形2.弦、弧、弦心距、圆心角之间的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
