【新课标】24.2.4圆的确定 课件(共42张PPT)
文档属性
| 名称 | 【新课标】24.2.4圆的确定 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 17:44:18 | ||
图片预览







文档简介
(共42张PPT)
24.2.4 圆的确定
沪科版 九年级下
教学内容分析
前面学习了圆的弦、弧、弦心距等概念,以及垂径定理,在圆的基本概念基础上,本节内容主要探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤。
教学目标
1. 掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆;(重点)
2.理解外接圆、外心的概念,会作出三角形的外接圆;(难点)
3.理解反证法证明的步骤。
核心素养分析
本节探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤,培养了学生几何直观的素养,以及推理的能力。
新知导入
圆心角、弦、弧、弦心距之间的关系是什么?
在同圆或等圆中,两个圆心角、弦、弧、弦心距之间,有一组量相等,其余各组量都相等。
新知讲解
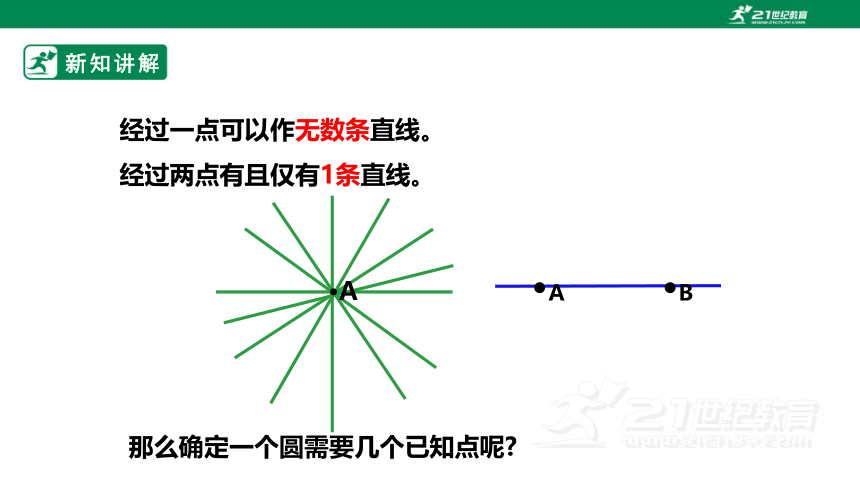
经过一点可以作无数条直线。
经过两点有且仅有1条直线。
·B
·A
·A
那么确定一个圆需要几个已知点呢
新知讲解
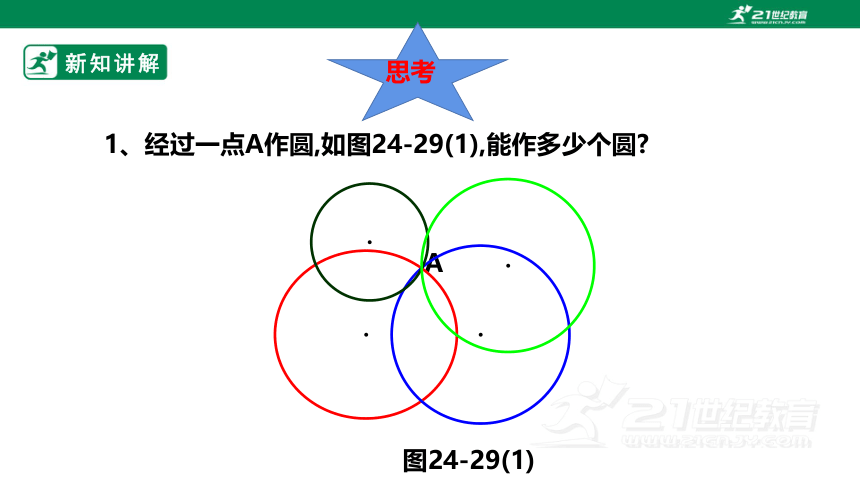
1、经过一点A作圆,如图24-29(1),能作多少个圆
思考
.A
图24-29(1)
·
·
·
·
新知讲解
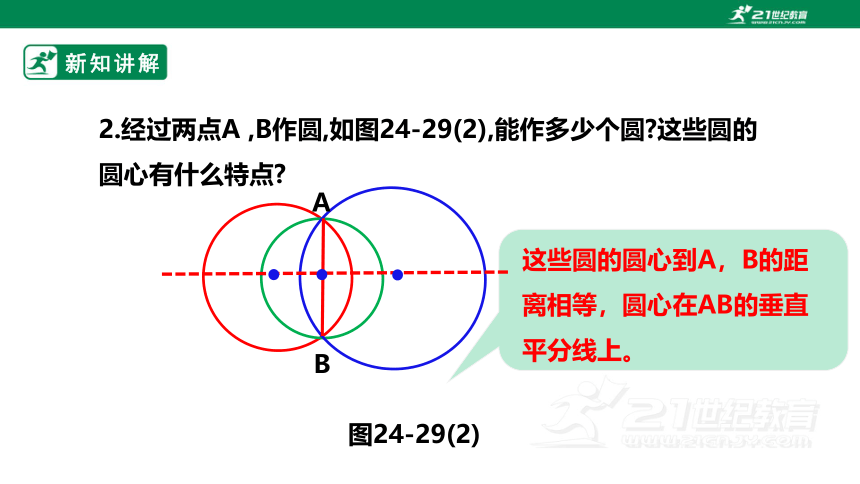
2.经过两点A ,B作圆,如图24-29(2),能作多少个圆 这些圆的圆心有什么特点
图24-29(2)
这些圆的圆心到A,B的距离相等,圆心在AB的垂直平分线上。
A
B
新知讲解
3.经过三点A,B ,C,能不能作圆
不一定
新知讲解
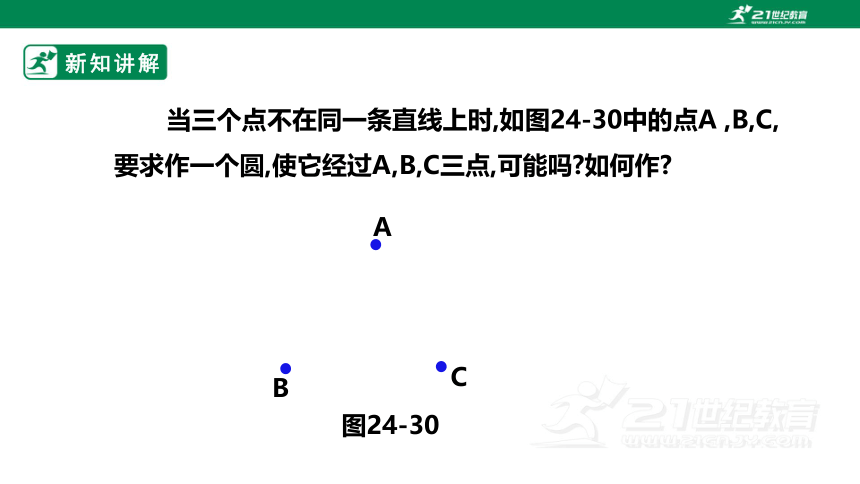
当三个点不在同一条直线上时,如图24-30中的点A ,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 如何作
A
B
C
图24-30
新知讲解
分析:经过不在同一条直线上的三点A,B,C能否作圆,
关键是看能否找到一点O,使OA=OB=OC.
若圆过A,B两点,圆心应在线段AB的垂直平分线上;
同理,若圆过B,C两点,圆心也应在线段BC的垂直平分线上.
所以AB ,BC两条线段的垂直平分线的交点О就是所找的点,
就是经过A,B,C三点的圆的圆心。
新知讲解
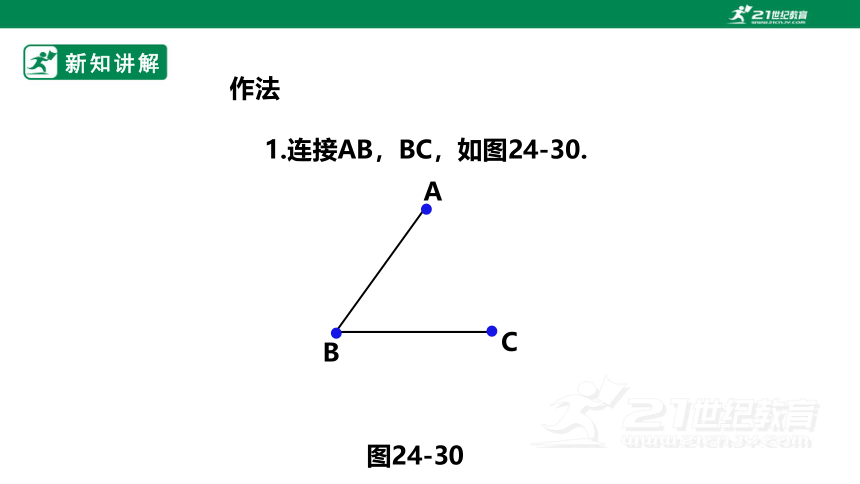
1.连接AB,BC,如图24-30.
A
B
C
图24-30
作法
新知讲解
2.分别作线段AB , BC的垂直平分线,设它们交于点О.
A
B
C
O
图24-30
新知讲解
3.以点О为圆心,OA为半径作圆,则☉O即为所作。
A
B
C
O
图24-30
不在同一直线上的三个点确定一个圆.
新知讲解
C
A
B
O
新知讲解
不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC
A
B
O
图24-30
C
三角形的外接圆
三角形的外心
圆的内接三角形
新知讲解
当三个点在同一条直线l上时,如图24-31中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗
A
B
C
图24-31
新知讲解
假设经过直线I上的三点A、B、C可以作圆,
设这个圆的圆心为O.
由OA =OB可知,点O在AB的垂直平分线l1上;
图24-31
A B C
l1
新知讲解
由OB=OC可知,点O也应在BC的垂直平分线l2上
图24-31
A B C
l1
l2
新知讲解
因为AB ,BC都在直线l上,
这样,经过点О便有两条直线l1、l2都垂直于直线l
图24-31
A B C
l1
l2
O
新知讲解
这与“过一点有且只有一条直线与已知直线垂直”相矛盾。
所以,经过同一条直线上的三点是不可以作圆的。
图24-31
A B C
l1
l2
O
新知讲解
这里的证明不是直接从题设推出结论,
而是先假设命题结论不成立,
然后经过推理,得出矛盾的结果,
最后断言结论一定成立,这样的证明方法叫做反证法.
用反证法证明命题的三个步骤:
(1)反设:假设命题的结论不成立;
(2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果;
(3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立.
新知讲解
新知讲解
已知:如图24-32,直线AB//直线CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.
图24-32
E
F
A B
C D
O1
O2
新知讲解
证明:假设∠EO1B≠∠EO2D,
过点O1作直线A'B',
使∠EO1B'=∠EO2D.
根据”同位角相等,两直线平行”,
得A'B'// CD.
图24-32
E
F
A B
C D
O1
O2
A'
B'
新知讲解
这样,过点O1就有两条直线AB,
A'B'平行于直线CD,
这与“过直线外一点有且只有一条直线
与这条直线平行”相矛盾,
即∠EO1B≠∠EO2D的假设不成立,
所以∠EO1B=∠EO2D.
图24-32
E
F
A B
C D
O1
O2
新知讲解
什么样的命题适合用反证法证明呢?
直接证明有困难
否定性命题
唯一性命题
至多、至少型命题
1、三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形外接圆的半径为_____
课堂练习
2.5
解:方程x2-12x+35=0,
分解因式得:(x-5)(x-7)=0,
可得x-5=0或x-7=0,
解得:x=5或x=7,
∵三角形第三边的长是方程x2-12x+35=0的根,
∴第三边的长为5或7,
当第三边长为5时,
∵3+4>5;
当第三边长为7时,3+4=7,不能构成三角形,舍去,
∴第三边为5,
∵32+42=52,
∴三角形是直角三角形,此三角形的外接圆的直径为最大边5,则此三角形的外接圆半径为2.5,
故答案为:2.5。
课堂练习
课堂练习
2.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,点O为坐标原点(网格纸中每个小正方形的边长为1).
(1)该图中弧所在圆的圆心D的坐标为____________.
(2,-1)
(2)根据(1)中的条件填空;
①⊙D的半径=____________(结果保留根号);
②点(-3,0)在⊙D__________.(填“上”、“内”或“外”);
③求出∠ADC的度数.
课堂练习
外
课堂练习
连接AD,CD,AC,
由平面直角坐标系得A(0,3),C(6,1),
∴
∵圆D的半径为 ,
∴AD=CD= ,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∠ADC=90°.
课堂练习
3.如图,已知⊙O是△ABC的外接圆,圆心O在△ABC的外部,AB=AC=4,BC= ,求⊙O的半径.
课堂练习
解:如图,连接AO,交BC于点D,连接BO
∵AB=AC,
∴AB=AC
又AO是半径,
∴AO⊥BC,BD=CD
∵BC= ,
∴BD=
课堂练习
∴在Rt△ABD中,
∠ADB=90°,
∴BD2+AD2=AB2
又∵AB=4,
∴AD=2
课堂练习
设半径为r.
在Rt△BDO中,
∵BD2+DO2=BO2
∴( )2+(r-2)2=r2
∴r=4
∴⊙O的半径为4.
不在同一直线上的三个点确定一个圆.
三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC
A
B
O
C
三角形的外接圆
三角形的外心
圆的内接三角形
课堂总结
课堂总结
用反证法证明命题三个步骤:
(1)反设:假设命题的结论不成立;
(2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果;
(3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立.
板书设计
24.2.4 圆的确定
1.不共线的三点确定一个圆
2.反证法
作业布置
必做题:课本P24的第2~4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.2.4 圆的确定
沪科版 九年级下
教学内容分析
前面学习了圆的弦、弧、弦心距等概念,以及垂径定理,在圆的基本概念基础上,本节内容主要探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤。
教学目标
1. 掌握经过一个点、2个点可以画圆,经过不共线的三点可以确定唯一的圆;(重点)
2.理解外接圆、外心的概念,会作出三角形的外接圆;(难点)
3.理解反证法证明的步骤。
核心素养分析
本节探究不在一条直线的三个点,可以确定一个圆,另外,学习了反证法证明命题的步骤,培养了学生几何直观的素养,以及推理的能力。
新知导入
圆心角、弦、弧、弦心距之间的关系是什么?
在同圆或等圆中,两个圆心角、弦、弧、弦心距之间,有一组量相等,其余各组量都相等。
新知讲解
经过一点可以作无数条直线。
经过两点有且仅有1条直线。
·B
·A
·A
那么确定一个圆需要几个已知点呢
新知讲解
1、经过一点A作圆,如图24-29(1),能作多少个圆
思考
.A
图24-29(1)
·
·
·
·
新知讲解
2.经过两点A ,B作圆,如图24-29(2),能作多少个圆 这些圆的圆心有什么特点
图24-29(2)
这些圆的圆心到A,B的距离相等,圆心在AB的垂直平分线上。
A
B
新知讲解
3.经过三点A,B ,C,能不能作圆
不一定
新知讲解
当三个点不在同一条直线上时,如图24-30中的点A ,B,C,要求作一个圆,使它经过A,B,C三点,可能吗 如何作
A
B
C
图24-30
新知讲解
分析:经过不在同一条直线上的三点A,B,C能否作圆,
关键是看能否找到一点O,使OA=OB=OC.
若圆过A,B两点,圆心应在线段AB的垂直平分线上;
同理,若圆过B,C两点,圆心也应在线段BC的垂直平分线上.
所以AB ,BC两条线段的垂直平分线的交点О就是所找的点,
就是经过A,B,C三点的圆的圆心。
新知讲解
1.连接AB,BC,如图24-30.
A
B
C
图24-30
作法
新知讲解
2.分别作线段AB , BC的垂直平分线,设它们交于点О.
A
B
C
O
图24-30
新知讲解
3.以点О为圆心,OA为半径作圆,则☉O即为所作。
A
B
C
O
图24-30
不在同一直线上的三个点确定一个圆.
新知讲解
C
A
B
O
新知讲解
不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC
A
B
O
图24-30
C
三角形的外接圆
三角形的外心
圆的内接三角形
新知讲解
当三个点在同一条直线l上时,如图24-31中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗
A
B
C
图24-31
新知讲解
假设经过直线I上的三点A、B、C可以作圆,
设这个圆的圆心为O.
由OA =OB可知,点O在AB的垂直平分线l1上;
图24-31
A B C
l1
新知讲解
由OB=OC可知,点O也应在BC的垂直平分线l2上
图24-31
A B C
l1
l2
新知讲解
因为AB ,BC都在直线l上,
这样,经过点О便有两条直线l1、l2都垂直于直线l
图24-31
A B C
l1
l2
O
新知讲解
这与“过一点有且只有一条直线与已知直线垂直”相矛盾。
所以,经过同一条直线上的三点是不可以作圆的。
图24-31
A B C
l1
l2
O
新知讲解
这里的证明不是直接从题设推出结论,
而是先假设命题结论不成立,
然后经过推理,得出矛盾的结果,
最后断言结论一定成立,这样的证明方法叫做反证法.
用反证法证明命题的三个步骤:
(1)反设:假设命题的结论不成立;
(2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果;
(3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立.
新知讲解
新知讲解
已知:如图24-32,直线AB//直线CD,直线EF分别交AB,CD于点O1,O2.
求证:∠EO1B=∠EO2D.
图24-32
E
F
A B
C D
O1
O2
新知讲解
证明:假设∠EO1B≠∠EO2D,
过点O1作直线A'B',
使∠EO1B'=∠EO2D.
根据”同位角相等,两直线平行”,
得A'B'// CD.
图24-32
E
F
A B
C D
O1
O2
A'
B'
新知讲解
这样,过点O1就有两条直线AB,
A'B'平行于直线CD,
这与“过直线外一点有且只有一条直线
与这条直线平行”相矛盾,
即∠EO1B≠∠EO2D的假设不成立,
所以∠EO1B=∠EO2D.
图24-32
E
F
A B
C D
O1
O2
新知讲解
什么样的命题适合用反证法证明呢?
直接证明有困难
否定性命题
唯一性命题
至多、至少型命题
1、三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形外接圆的半径为_____
课堂练习
2.5
解:方程x2-12x+35=0,
分解因式得:(x-5)(x-7)=0,
可得x-5=0或x-7=0,
解得:x=5或x=7,
∵三角形第三边的长是方程x2-12x+35=0的根,
∴第三边的长为5或7,
当第三边长为5时,
∵3+4>5;
当第三边长为7时,3+4=7,不能构成三角形,舍去,
∴第三边为5,
∵32+42=52,
∴三角形是直角三角形,此三角形的外接圆的直径为最大边5,则此三角形的外接圆半径为2.5,
故答案为:2.5。
课堂练习
课堂练习
2.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,点O为坐标原点(网格纸中每个小正方形的边长为1).
(1)该图中弧所在圆的圆心D的坐标为____________.
(2,-1)
(2)根据(1)中的条件填空;
①⊙D的半径=____________(结果保留根号);
②点(-3,0)在⊙D__________.(填“上”、“内”或“外”);
③求出∠ADC的度数.
课堂练习
外
课堂练习
连接AD,CD,AC,
由平面直角坐标系得A(0,3),C(6,1),
∴
∵圆D的半径为 ,
∴AD=CD= ,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∠ADC=90°.
课堂练习
3.如图,已知⊙O是△ABC的外接圆,圆心O在△ABC的外部,AB=AC=4,BC= ,求⊙O的半径.
课堂练习
解:如图,连接AO,交BC于点D,连接BO
∵AB=AC,
∴AB=AC
又AO是半径,
∴AO⊥BC,BD=CD
∵BC= ,
∴BD=
课堂练习
∴在Rt△ABD中,
∠ADB=90°,
∴BD2+AD2=AB2
又∵AB=4,
∴AD=2
课堂练习
设半径为r.
在Rt△BDO中,
∵BD2+DO2=BO2
∴( )2+(r-2)2=r2
∴r=4
∴⊙O的半径为4.
不在同一直线上的三个点确定一个圆.
三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC
A
B
O
C
三角形的外接圆
三角形的外心
圆的内接三角形
课堂总结
课堂总结
用反证法证明命题三个步骤:
(1)反设:假设命题的结论不成立;
(2)推理:从(1)中的“反设”出发,逐步推理直至出现与已知条件、定义、基本事实、定理等中任一个相矛盾的结果;
(3)结论:由矛盾的结果判定(1)中的“反设”不成立,从而肯定命题的结论成立.
板书设计
24.2.4 圆的确定
1.不共线的三点确定一个圆
2.反证法
作业布置
必做题:课本P24的第2~4题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
