2.5.1二次函数与一元二次方程 教案
图片预览



文档简介
中小学教育资源及组卷应用平台
2.5.1二次函数与一元二次方程 教学设计
课题 2.5.1二次函数与一元二次方程 单元 第2 单元 学科 数学 年级 九年级(下)
教材分析 本节课学习二次函数与一元二次方程之间的关系,将从方程知识“数”的层面进一步认识二次函数,也就是用数形结合的数学思想来认识二次函数.通过二次函数图像与一元二次方程之间关系的探究活动,体会二次函数与一元二次方程之间的联系,理解二次函数与一元二次方程的关系,会判断抛物线与x轴交点的个数、掌握方程与函数间的转化.
核心素养分析 逐步探索二次函数与一元二次方程之间的关系,函数图像与x轴的交点情况。由特殊到一般,提高学生的分析、探索归纳能力,进一步培养学生的数形结合思想.
学习目标 1.理解二次函数的图象与x轴交点的个数与一元二次方程根的个数之间的对应关系;2.会利用二次函数的图象与x轴交点的横坐标解相应的一元二次方程.
重点 探索二次函数图像与一元二次方程的关系,理解抛物线与x轴交点情况.
难点 函数→方程→x轴交点,三者之间的理解与运用.
教学过程
教学环节 教师活动 学生活动 设计意图
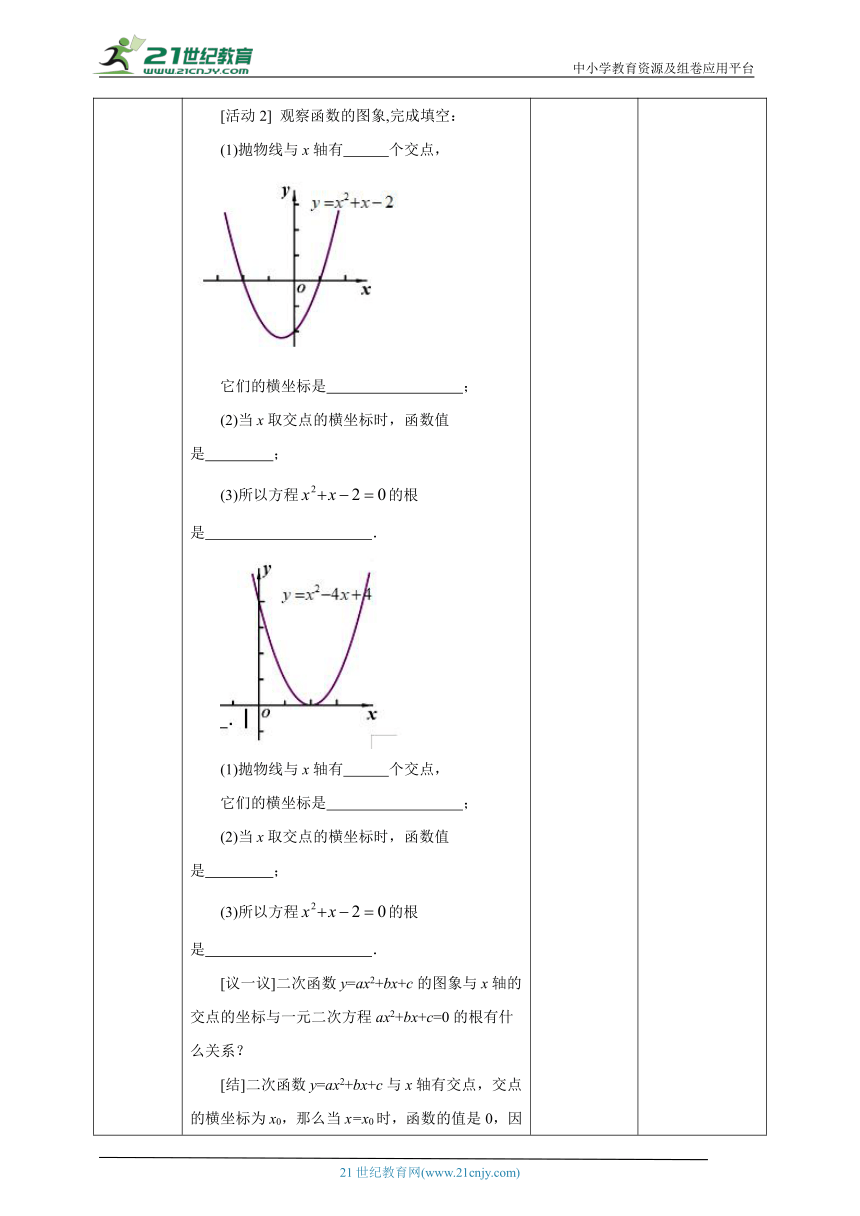
导入新课 一、创设情景,引出课题第一环节:学科交叉,发现问题我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面被以40m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,观察并思考下列问题:(1)h和t的关系式是什么?(2)小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.[方法一]看图象可知,8秒落地[方法二]解方程:第二环节:建立模型,分析问题[活动1] 二次函数的图象如下图所示,与同伴交流并回答问题.第三环节:反思辨析,深入问题[活动2] 观察函数的图象,完成填空:(1)抛物线与x轴有 个交点,它们的横坐标是 ;(2)当x取交点的横坐标时,函数值是 ;(3)所以方程的根是 .(1)抛物线与x轴有 个交点,它们的横坐标是 ;(2)当x取交点的横坐标时,函数值是 ;(3)所以方程的根是 .[议一议]二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?[结]二次函数y=ax2+bx+c与x轴有交点,交点的横坐标为x0,那么当x=x0时,函数的值是0,因此x=x0就是方程ax2+bx+c=0的根.即,二次函数y=ax2+bx+c与x轴交点的横坐标是方程ax2+bx+c=0的根. 思考自议体会二次函数与方程之间的联系. 理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系.
讲授新课 提炼概念第四环节:数形结合,解决问题[议一议]二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数y=ax2+bx+c的图 一元二次方程ax2+bx+c=0象和x轴交点有三种情况: 的根有三种情况:有两个交点 有两个不相等的实数根有一个交点 有两个相等的实数根没有交点 没有实数根典例精讲 例:何时小球离地面的高度是60m?你是如何知道的?解法1:令h=60故2s和6s时,小球离地面的高度是60m.解法2:看图象.不用计算,小球离地面的高度可能是100m吗 为什么 理解一元二次方程的根就是二次函数与x轴 交点的横坐标. 对二次函数与一元二次方程的关系的认识,是否理解了理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系.
课堂练习 四、巩固训练1.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).A.无解 B.x=1C.x=-4 D.x=-1或x=4D2.求下列二次函数的图像与x轴的交点.(1)y=x2+4x-5(2)y=-x2+x+23.二次函数y=x2+bx-1的图象与x轴相交吗?如果相交,有几个交点?解:∵ =b2-4×1×(-1)=b2+4>0∴二次函数y=x2+bx-1的图象与x轴相交,有2个交点. 4. 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来。就是直线与二次函数图象交点的横坐标。5.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.解:当k≠3时,y=(k-3)x2+2x+1是二次函数. 若二次函数y=(k-3)x2+2x+1的图象与x轴有交点, 则一元二次方程(k-3)x2+2x+1=0 中Δ≥0. 即 b2-4ac = 22-4(k-3) = -4k+16 ≥0 解得 k≤4 ∴k≤4且k≠3. 当k=3时,函数y=2x+1是一次函数,与x轴有一个交点, 符合题意; 综上所述,k的取值范围是k≤4.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
2.5.1二次函数与一元二次方程 教学设计
课题 2.5.1二次函数与一元二次方程 单元 第2 单元 学科 数学 年级 九年级(下)
教材分析 本节课学习二次函数与一元二次方程之间的关系,将从方程知识“数”的层面进一步认识二次函数,也就是用数形结合的数学思想来认识二次函数.通过二次函数图像与一元二次方程之间关系的探究活动,体会二次函数与一元二次方程之间的联系,理解二次函数与一元二次方程的关系,会判断抛物线与x轴交点的个数、掌握方程与函数间的转化.
核心素养分析 逐步探索二次函数与一元二次方程之间的关系,函数图像与x轴的交点情况。由特殊到一般,提高学生的分析、探索归纳能力,进一步培养学生的数形结合思想.
学习目标 1.理解二次函数的图象与x轴交点的个数与一元二次方程根的个数之间的对应关系;2.会利用二次函数的图象与x轴交点的横坐标解相应的一元二次方程.
重点 探索二次函数图像与一元二次方程的关系,理解抛物线与x轴交点情况.
难点 函数→方程→x轴交点,三者之间的理解与运用.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题第一环节:学科交叉,发现问题我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面被以40m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t(s)的关系如图所示,观察并思考下列问题:(1)h和t的关系式是什么?(2)小球经过多少秒后落地 你有几种求解方法 与同伴进行交流.[方法一]看图象可知,8秒落地[方法二]解方程:第二环节:建立模型,分析问题[活动1] 二次函数的图象如下图所示,与同伴交流并回答问题.第三环节:反思辨析,深入问题[活动2] 观察函数的图象,完成填空:(1)抛物线与x轴有 个交点,它们的横坐标是 ;(2)当x取交点的横坐标时,函数值是 ;(3)所以方程的根是 .(1)抛物线与x轴有 个交点,它们的横坐标是 ;(2)当x取交点的横坐标时,函数值是 ;(3)所以方程的根是 .[议一议]二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?[结]二次函数y=ax2+bx+c与x轴有交点,交点的横坐标为x0,那么当x=x0时,函数的值是0,因此x=x0就是方程ax2+bx+c=0的根.即,二次函数y=ax2+bx+c与x轴交点的横坐标是方程ax2+bx+c=0的根. 思考自议体会二次函数与方程之间的联系. 理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系.
讲授新课 提炼概念第四环节:数形结合,解决问题[议一议]二次函数y=ax2+bx+c的图象与x轴的交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数y=ax2+bx+c的图 一元二次方程ax2+bx+c=0象和x轴交点有三种情况: 的根有三种情况:有两个交点 有两个不相等的实数根有一个交点 有两个相等的实数根没有交点 没有实数根典例精讲 例:何时小球离地面的高度是60m?你是如何知道的?解法1:令h=60故2s和6s时,小球离地面的高度是60m.解法2:看图象.不用计算,小球离地面的高度可能是100m吗 为什么 理解一元二次方程的根就是二次函数与x轴 交点的横坐标. 对二次函数与一元二次方程的关系的认识,是否理解了理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系.
课堂练习 四、巩固训练1.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).A.无解 B.x=1C.x=-4 D.x=-1或x=4D2.求下列二次函数的图像与x轴的交点.(1)y=x2+4x-5(2)y=-x2+x+23.二次函数y=x2+bx-1的图象与x轴相交吗?如果相交,有几个交点?解:∵ =b2-4×1×(-1)=b2+4>0∴二次函数y=x2+bx-1的图象与x轴相交,有2个交点. 4. 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来。就是直线与二次函数图象交点的横坐标。5.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.解:当k≠3时,y=(k-3)x2+2x+1是二次函数. 若二次函数y=(k-3)x2+2x+1的图象与x轴有交点, 则一元二次方程(k-3)x2+2x+1=0 中Δ≥0. 即 b2-4ac = 22-4(k-3) = -4k+16 ≥0 解得 k≤4 ∴k≤4且k≠3. 当k=3时,函数y=2x+1是一次函数,与x轴有一个交点, 符合题意; 综上所述,k的取值范围是k≤4.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
