2.5.1二次函数与一元二次方程 课件(共20张PPT)
文档属性
| 名称 | 2.5.1二次函数与一元二次方程 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 19:22:46 | ||
图片预览








文档简介
(共20张PPT)
2.5.1二次函数与一元二次方程
北师大版 九年级 下册
教学目标
教学目标:1.经历探索二次函数与一元二次方程的关系的过程,体会方程
与函数之间的联系.
2.理解二次函数的图象和横轴交点的个数与一元二次方程的根
的个数之间的关系,理解何时方程有两个不相等的实数根、
两个相等的实数根和没有实数根.
教学重点:探索二次函数图像与一元二次方程的关系,理解抛物线与x轴交
点情况.
教学难点:函数→方程→x轴交点,三者之间的理解与运用.
我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0,且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢?本节课我们将探索有关问题.
新知讲解
合作学习
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么
情景引入
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?你有几种求解方法?
解:(1)由题意得:h0=0,v0=40
∴h=-5t2+40t
合作学习
(2)小球经过多少秒后落地?你有几种求解方法?
(2)法一:由图像可知小球经过8s后落地.
法二:令h=0得
-5t2+40t=0
解得t1=0(舍)t2=8
答:小球经过8s后落地.
h=-5t2+40t
活动探究
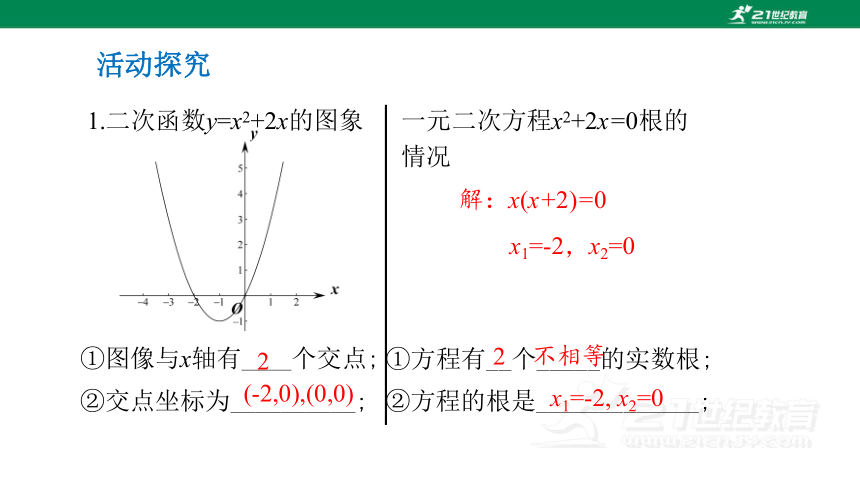
1.二次函数y=x2+2x的图象
①图像与x轴有____个交点;
②交点坐标为__________;
一元二次方程x2+2x=0根的情况
①方程有__个_____的实数根;
②方程的根是_____________;
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0
2.二次函数y=x2-2x+1的图象
①图像与x轴有____个交点;
②交点坐标为________;
一元二次方程x2-2x+1=0根的情况
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1
3.二次函数y=x2-2x+2的图象
图像与x轴没有交点;
一元二次方程x2-2x+2=0根的情况
方程没有实数根;
=b2-4ac
=(-2)2-4×1×2
=-4<0
提炼概念
二次函数图像与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根;
2个交点;
1个交点;
方程2个不相等实数根;
典例精讲
例: 本节开始时小球上抛问题中,何时小球离地面的高度是60m呢?你是如何知道的.
解:法1.由题意将h=60代入h=-5t2+40t中
-5t2+40t=60
解得t1=2, t2=6
法2.由图像可知:
直线h=60
(2,60)
(6,60)
2s和6s时小球离地面的高度是60m.
数形结合
不用计算,小球离地面的高度可能是100m吗 为什么
归纳概念
二次函数y=ax2+bx+c的图像 二次函数y=ax2+bx+c的图像与x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式 =b2-4ac
有2个交点
有两个不相等的实数根
b2-4ac>0
有1个交点
有两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
结论2:二次函数y=ax2+bx+c的图像与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
结论1:
课堂练习
1.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
D
2.求下列二次函数的图像与x轴的交点.
解:(1)当y=0,
0=x2+4x-5
(1)y=x2+4x-5
解得x1=-5, x2=1
所以二次函数与x轴的交点为 (-5,0), (1,0)
(2)当y=0,
0=-x2+x+2
解得x1=-1, x2=2
所以二次函数与x轴的交点为 (-1,0), (2,0)
(2)y=-x2+x+2
3.二次函数y=x2+bx-1的图象与x轴相交吗?如果相交,有几个交点?
解:∵ =b2-4×1×(-1)
=b2+4
>0
∴二次函数y=x2+bx-1的图象与x轴相交,有2个交点.
1
0
1
x
y
M
N
2
3
2
y=x2-4x+4
4. 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来.
5.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.
解:当k≠3时,y=(k-3)x2+2x+1是二次函数.
若二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
则一元二次方程(k-3)x2+2x+1=0 中Δ≥0.
即 b2-4ac = 22-4(k-3) = -4k+16 ≥0
解得 k≤4
∴k≤4且k≠3.
当k=3时,函数y=2x+1是一次函数,与x轴有一个交点,
符合题意;
综上所述,k的取值范围是k≤4.
课堂总结
二次函数y=ax2+bx+c的图像与x轴的交点有三种情况:有两个交点、有一个交点、没有交点.
与此相对应一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、没有实数根.
二次函数y=ax2+bx+c的图像与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
二次函数与一元二次方程的关系,体现了“数形结合”这一重要的数学思想方法.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.5.1二次函数与一元二次方程
北师大版 九年级 下册
教学目标
教学目标:1.经历探索二次函数与一元二次方程的关系的过程,体会方程
与函数之间的联系.
2.理解二次函数的图象和横轴交点的个数与一元二次方程的根
的个数之间的关系,理解何时方程有两个不相等的实数根、
两个相等的实数根和没有实数根.
教学重点:探索二次函数图像与一元二次方程的关系,理解抛物线与x轴交
点情况.
教学难点:函数→方程→x轴交点,三者之间的理解与运用.
我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0,且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢?本节课我们将探索有关问题.
新知讲解
合作学习
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么
情景引入
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?你有几种求解方法?
解:(1)由题意得:h0=0,v0=40
∴h=-5t2+40t
合作学习
(2)小球经过多少秒后落地?你有几种求解方法?
(2)法一:由图像可知小球经过8s后落地.
法二:令h=0得
-5t2+40t=0
解得t1=0(舍)t2=8
答:小球经过8s后落地.
h=-5t2+40t
活动探究
1.二次函数y=x2+2x的图象
①图像与x轴有____个交点;
②交点坐标为__________;
一元二次方程x2+2x=0根的情况
①方程有__个_____的实数根;
②方程的根是_____________;
2
(-2,0),(0,0)
2
不相等
x1=-2, x2=0
解:x(x+2)=0
x1=-2,x2=0
2.二次函数y=x2-2x+1的图象
①图像与x轴有____个交点;
②交点坐标为________;
一元二次方程x2-2x+1=0根的情况
1
(1,0)
2
相等
x1=x2=1
解:(x-1)2=0
x1=x2=1
3.二次函数y=x2-2x+2的图象
图像与x轴没有交点;
一元二次方程x2-2x+2=0根的情况
方程没有实数根;
=b2-4ac
=(-2)2-4×1×2
=-4<0
提炼概念
二次函数图像与x轴的交点坐标
y=x2+2x
y=x2-2x+1
y=x2-2x+2
x2+2x=0
x2-2x+1=0
x2-2x+2=0
一元二次方程的根
(-2,0),(0,0)
(1,0)
没有交点;
x1=-2, x2=0
x1=x2=1
方程没有实数根;
2个交点;
1个交点;
方程2个不相等实数根;
典例精讲
例: 本节开始时小球上抛问题中,何时小球离地面的高度是60m呢?你是如何知道的.
解:法1.由题意将h=60代入h=-5t2+40t中
-5t2+40t=60
解得t1=2, t2=6
法2.由图像可知:
直线h=60
(2,60)
(6,60)
2s和6s时小球离地面的高度是60m.
数形结合
不用计算,小球离地面的高度可能是100m吗 为什么
归纳概念
二次函数y=ax2+bx+c的图像 二次函数y=ax2+bx+c的图像与x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式 =b2-4ac
有2个交点
有两个不相等的实数根
b2-4ac>0
有1个交点
有两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
结论2:二次函数y=ax2+bx+c的图像与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
结论1:
课堂练习
1.小明画了一个函数y=x2+ax+b的图象如图所示,则关于x的方程x2+ax+b=0的解是( ).
A.无解 B.x=1
C.x=-4 D.x=-1或x=4
D
2.求下列二次函数的图像与x轴的交点.
解:(1)当y=0,
0=x2+4x-5
(1)y=x2+4x-5
解得x1=-5, x2=1
所以二次函数与x轴的交点为 (-5,0), (1,0)
(2)当y=0,
0=-x2+x+2
解得x1=-1, x2=2
所以二次函数与x轴的交点为 (-1,0), (2,0)
(2)y=-x2+x+2
3.二次函数y=x2+bx-1的图象与x轴相交吗?如果相交,有几个交点?
解:∵ =b2-4×1×(-1)
=b2+4
>0
∴二次函数y=x2+bx-1的图象与x轴相交,有2个交点.
1
0
1
x
y
M
N
2
3
2
y=x2-4x+4
4. 一元二次方程x2-4x+4=1的根与二次函数y=x2-4x+4的图象有什么关系?试把方程的根在图象上表示出来.
5.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,求k的取值范围.
解:当k≠3时,y=(k-3)x2+2x+1是二次函数.
若二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
则一元二次方程(k-3)x2+2x+1=0 中Δ≥0.
即 b2-4ac = 22-4(k-3) = -4k+16 ≥0
解得 k≤4
∴k≤4且k≠3.
当k=3时,函数y=2x+1是一次函数,与x轴有一个交点,
符合题意;
综上所述,k的取值范围是k≤4.
课堂总结
二次函数y=ax2+bx+c的图像与x轴的交点有三种情况:有两个交点、有一个交点、没有交点.
与此相对应一元二次方程ax2+bx+c=0的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、没有实数根.
二次函数y=ax2+bx+c的图像与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
二次函数与一元二次方程的关系,体现了“数形结合”这一重要的数学思想方法.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
