北师大版八年级上册 1.2一定是直角三角形吗 课件(共26张PPT)
文档属性
| 名称 | 北师大版八年级上册 1.2一定是直角三角形吗 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 06:22:03 | ||
图片预览







文档简介
(共26张PPT)
一定是直角三角形吗
4
3
4
∟
3
4
5
5
3
4
5
∟
32+42=25=52
已知:Rt
根据勾股定理
Rt
已知:32+42=52
5
12
13
13
∟
52+122=169=132
已知:Rt
根据勾股定理
Rt
已知:52+122=132
12
∟
5
∟
b
∟
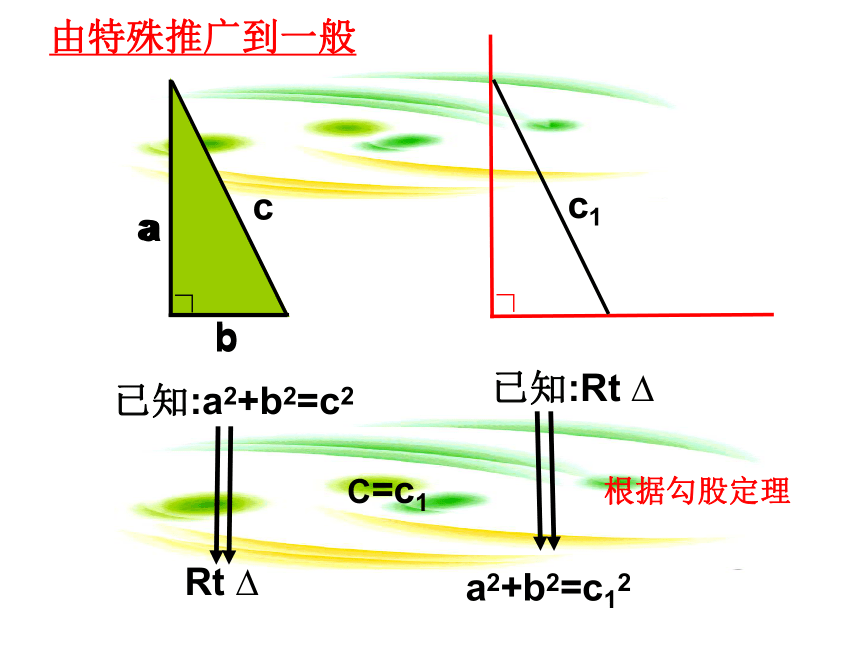
由特殊推广到一般
已知:a2+b2=c2
Rt
a
c
a
c1
a
C=c1
b
a2+b2=c12
已知:Rt
根据勾股定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是 直角三角形.
且最长边c所对的角是直角
结论:
c
a
b
变式: c2-b2 =a2 c2-a2 =b2
Rt
∟
例1
边长为7,24, 25的三角形是直角三角形吗
∵72+242=49+576=625
252 =625
∴72+242= 252
或252-242=(25+24)(25 -24) =49=72
2练习
下列几组数能否作为直角三角形的三边长?
( 说明理由)
(1)8,15,17(2)6,8,10
(3)9,12,15 (4)11,60,61
(5)12,18,22
fangwei.swf
三边长为3n,4n,5n ( ) 的三角形
(1)是不是直角三角形(2)是不是勾股数
9,12,15
6,8,10
3,4,5; 5,12,13; 7,24,25; 8,15,17
满足a2 +b2=c2的三个
正整数, 称为勾股数
(3n)2+(4n)2=25n2=(5n)2
勾股数扩大n (n为正整数)倍,还是勾股数
n为正整数
1小显身手
1下列几组数能否作为直角三角形的三边长?
( 说明理由)
(1)0.3,0.5,0.4(2)30,40,50(2)32 ,42 , 52
(3)
2:以上哪些是勾股数
3
1
—,
4
1
—,
1
5
—
fangwei.swf
A
B
C
.
∵(6k)2+(8k)2=100k2 =(10k)2
∴∠B=900
∵ A → B是正东,∴B → C是正北.
AB:BC:AC=8:6:10
2大显身手
西→东
解:设AB=8k,BC=6k,AC=10k
在草坪上截出三角形草坪
勾几1.gsp
B
D
C
A
∟
3综合应用
1:三角形三边满足:
a2 +b2=c2
c2-b2 =a2
c2-a2 =b2
以它们为边的正方形就能围成直角三角形
4探究
思考: 三个正方形的面积 为 S1 ,S2 ,S3(S3最大)满足什么条件时能围成一个直角三角形
S1+S2=S3
S3-S2=S1
S3-S1=S2
64
225
289
∟
1 面积为64,225,289的三个正方形能否围成一个直角三角形
64+225=289
289-225=64
100
225
289
64
2 用面积为36和100的两个正方形草坪和图中哪个正方形草坪 能围成一个直角三角形呢
36
64
∟
∟
36+100=136
100-36=64
100
225
289
64
36
81
3 用面积为81和面积为多少的正方形草坪,与图中面积为225的正方形草坪围成一个直角三角形呢
9,12,15
144
225-81=144
225+81=306
306
∟
∟
∟
二班树
3满足a2 +b2=c2的三个正整数,称为勾股数
4勾股数扩大n(n为正整数)倍,还是勾股数 .
5会根据题意正确选择勾股定理或逆定理解
决问题
2会通过边的关系判断直角三角形
1用数形结合的思想得到,如果三角形的三边长a,b,c满足a 2+b2=c2 ,那么这个三角形是直角三角形
数形结合
特殊到一般
解决实际问题
勾股数,即变化规律
a 2+b2=c2→Rt
抽象数学模型
实际背景
抽象出
由一般到特殊
总结规律
网格中判断三角形形状
A
B
C
.
∵(6k)2+(8k)2=100k2 =(10k)2
∴∠B=900
∵ A → B是正东,∴B → C是正北.
AB:BC:AC=8:6:10
大显身手
西→东
解:设AB=8k,BC=6k,AC=10k
在草坪上截出三角形草坪
勾几1.gsp
勾几2.gsp
B
无标题-1.swf
D
C
A
∟
3满足a2 +b2=c2的三个正整数,称为勾股数
4勾股数扩大n(n为正整数)倍,还是勾股数 .
5会根据题意正确选择勾股定理或逆定理解
决问题
2会通过边的关系判断直角三角形
1用数形结合的思想得到,如果三角形的三边长a,b,c满足a 2+b2=c2 ,那么这个三角形是直角三角形
数形结合
特殊到一般
解决实际问题
勾股数,即变化规律
a 2+b2=c2→Rt
抽象数学模型
实际背景
抽象出
由一般到特殊
总结规律
网格中判断三角形形状
再见
一定是直角三角形吗
4
3
4
∟
3
4
5
5
3
4
5
∟
32+42=25=52
已知:Rt
根据勾股定理
Rt
已知:32+42=52
5
12
13
13
∟
52+122=169=132
已知:Rt
根据勾股定理
Rt
已知:52+122=132
12
∟
5
∟
b
∟
由特殊推广到一般
已知:a2+b2=c2
Rt
a
c
a
c1
a
C=c1
b
a2+b2=c12
已知:Rt
根据勾股定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是 直角三角形.
且最长边c所对的角是直角
结论:
c
a
b
变式: c2-b2 =a2 c2-a2 =b2
Rt
∟
例1
边长为7,24, 25的三角形是直角三角形吗
∵72+242=49+576=625
252 =625
∴72+242= 252
或252-242=(25+24)(25 -24) =49=72
2练习
下列几组数能否作为直角三角形的三边长?
( 说明理由)
(1)8,15,17(2)6,8,10
(3)9,12,15 (4)11,60,61
(5)12,18,22
fangwei.swf
三边长为3n,4n,5n ( ) 的三角形
(1)是不是直角三角形(2)是不是勾股数
9,12,15
6,8,10
3,4,5; 5,12,13; 7,24,25; 8,15,17
满足a2 +b2=c2的三个
正整数, 称为勾股数
(3n)2+(4n)2=25n2=(5n)2
勾股数扩大n (n为正整数)倍,还是勾股数
n为正整数
1小显身手
1下列几组数能否作为直角三角形的三边长?
( 说明理由)
(1)0.3,0.5,0.4(2)30,40,50(2)32 ,42 , 52
(3)
2:以上哪些是勾股数
3
1
—,
4
1
—,
1
5
—
fangwei.swf
A
B
C
.
∵(6k)2+(8k)2=100k2 =(10k)2
∴∠B=900
∵ A → B是正东,∴B → C是正北.
AB:BC:AC=8:6:10
2大显身手
西→东
解:设AB=8k,BC=6k,AC=10k
在草坪上截出三角形草坪
勾几1.gsp
B
D
C
A
∟
3综合应用
1:三角形三边满足:
a2 +b2=c2
c2-b2 =a2
c2-a2 =b2
以它们为边的正方形就能围成直角三角形
4探究
思考: 三个正方形的面积 为 S1 ,S2 ,S3(S3最大)满足什么条件时能围成一个直角三角形
S1+S2=S3
S3-S2=S1
S3-S1=S2
64
225
289
∟
1 面积为64,225,289的三个正方形能否围成一个直角三角形
64+225=289
289-225=64
100
225
289
64
2 用面积为36和100的两个正方形草坪和图中哪个正方形草坪 能围成一个直角三角形呢
36
64
∟
∟
36+100=136
100-36=64
100
225
289
64
36
81
3 用面积为81和面积为多少的正方形草坪,与图中面积为225的正方形草坪围成一个直角三角形呢
9,12,15
144
225-81=144
225+81=306
306
∟
∟
∟
二班树
3满足a2 +b2=c2的三个正整数,称为勾股数
4勾股数扩大n(n为正整数)倍,还是勾股数 .
5会根据题意正确选择勾股定理或逆定理解
决问题
2会通过边的关系判断直角三角形
1用数形结合的思想得到,如果三角形的三边长a,b,c满足a 2+b2=c2 ,那么这个三角形是直角三角形
数形结合
特殊到一般
解决实际问题
勾股数,即变化规律
a 2+b2=c2→Rt
抽象数学模型
实际背景
抽象出
由一般到特殊
总结规律
网格中判断三角形形状
A
B
C
.
∵(6k)2+(8k)2=100k2 =(10k)2
∴∠B=900
∵ A → B是正东,∴B → C是正北.
AB:BC:AC=8:6:10
大显身手
西→东
解:设AB=8k,BC=6k,AC=10k
在草坪上截出三角形草坪
勾几1.gsp
勾几2.gsp
B
无标题-1.swf
D
C
A
∟
3满足a2 +b2=c2的三个正整数,称为勾股数
4勾股数扩大n(n为正整数)倍,还是勾股数 .
5会根据题意正确选择勾股定理或逆定理解
决问题
2会通过边的关系判断直角三角形
1用数形结合的思想得到,如果三角形的三边长a,b,c满足a 2+b2=c2 ,那么这个三角形是直角三角形
数形结合
特殊到一般
解决实际问题
勾股数,即变化规律
a 2+b2=c2→Rt
抽象数学模型
实际背景
抽象出
由一般到特殊
总结规律
网格中判断三角形形状
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
