北师大版八年级上册1.3勾股定理的应用 课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级上册1.3勾股定理的应用 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 528.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 23:12:15 | ||
图片预览




文档简介
(共15张PPT)
1.3 勾股定理的应用
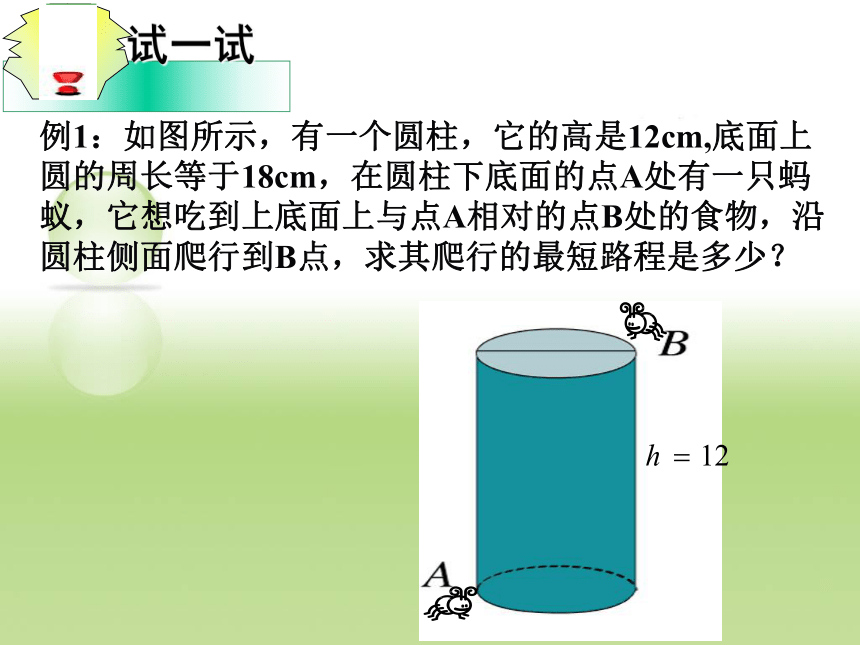
例1:如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
试一试
请大家尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?
议一议
如果将圆柱侧面剪开展开成一个长方形,从A点到B 点的最短路线是什么 你画对了吗
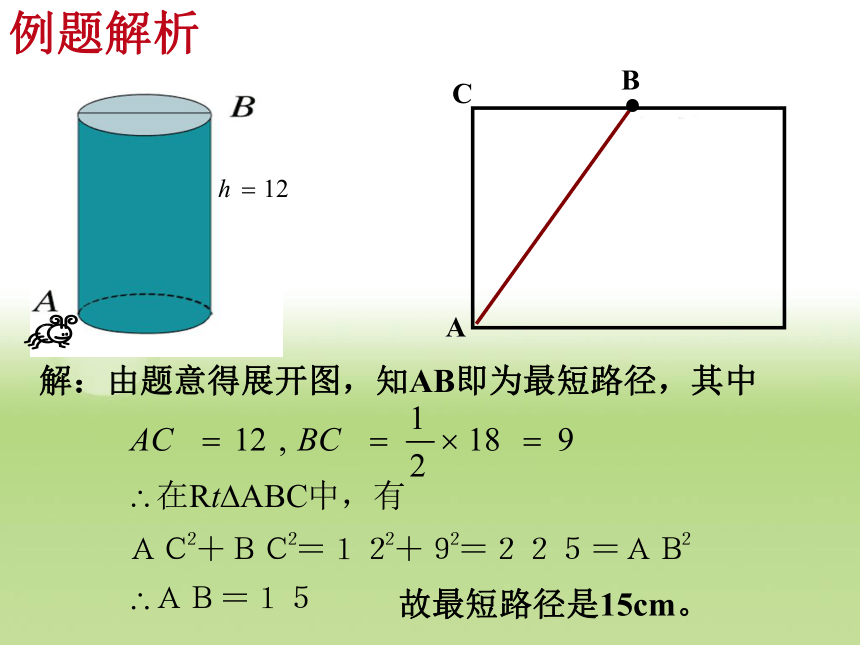
例题解析
C
解:由题意得展开图,知AB即为最短路径,其中
故最短路径是15cm。
B
A
归纳
解决几何体表面上两点之间的最短距离问题的关键是要设法把立体图形转化为平面图形,具体步骤是:
(1)把立体图形展成平面图形;
(2)确定点的位置;
(3)确定直角三角形;
(4)分析直角三角形的边长,用勾股定理求解.
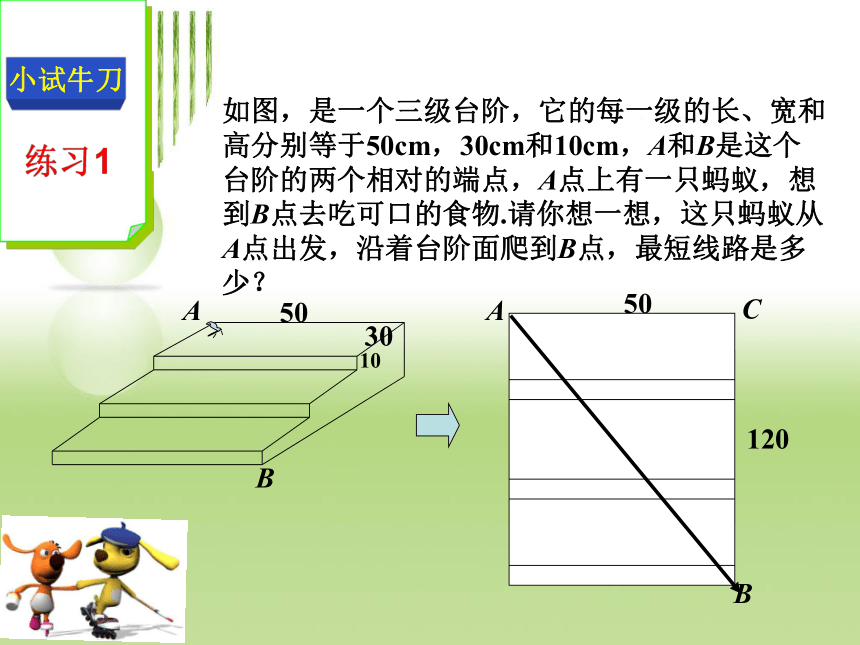
如图,是一个三级台阶,它的每一级的长、宽和高分别等于50cm,30cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
50
30
10
50
120
小试牛刀
例2 李叔叔想检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,随身只带了一把卷尺,
(1)你能替他想办法完成任务吗?
(2)量得AD长是30厘米,AB长是40厘米,BD长是50厘米。AD边垂直于AB边吗?
A
C
D
B
做一做
(3)如果李叔叔随身只有一个长度为20厘米的刻度尺,能有办法检验AD边是否垂直于AB边吗?边BC与边AB呢?
勾股定理与它的逆定理在应用上有什么区别?
议一议
勾股定理主要应用于在直角三角形中求线段
的长度,甚至周长或面积。
勾股定理的逆定理应用于根据三边的长度判断
三角形的形状。
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题,“今有池方一丈,葭生其中央,出水一尺。引葭赴岸,适与岸齐。问水深、葭长各几何?”这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?
试一试
中国人民的聪明智慧真的让人叹服!
5
解:设水池的深度为x尺,则芦苇的长度为 x+1尺。
x
x+1
由勾股定理得
x2 +52=(x+1)2
x=12
x2 +25= x2+2x+1
24= 2x
答:水池的深度为12尺,芦苇的长度为13尺
x+1=13(尺)
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长。已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长
小试牛刀
交流小结
通过本节课的学习,我们学习了哪些知识内容?
1.勾股定理在实际生活中的应用;
2.数学思想:
转化
实际问题
小结
方程思想,数形结合思想
数学问题
用勾股定理解决实际问题的具体步骤:
1.审题,分析实际问题;
2.把实际问题转化为数学问题;
3.运用勾股定理计算;
4.检验是否符合实际问题的真实性。
作 业:
P14 习题1.4 第1,3,4题
课外思考题:
学而不思则惘
B
A
2.如果蚂蚁处于的位置是一个长、宽、高分别为5、4、3的长
方体的左下端A,它到右上端B的最短路线该怎样选择呢?
1. 八(9)班的学生想知道学校旗杆的高度,他们发现旗杆上的绳子垂到地面还多2米,如图(1),你能帮他们把旗杆的高度和绳子的长度计算出来吗?
感谢可爱的孩子们
再 见
1.3 勾股定理的应用
例1:如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?
试一试
请大家尝试从A点到B点沿圆柱的侧面画出几条路线,你觉得哪条路线最短呢?
议一议
如果将圆柱侧面剪开展开成一个长方形,从A点到B 点的最短路线是什么 你画对了吗
例题解析
C
解:由题意得展开图,知AB即为最短路径,其中
故最短路径是15cm。
B
A
归纳
解决几何体表面上两点之间的最短距离问题的关键是要设法把立体图形转化为平面图形,具体步骤是:
(1)把立体图形展成平面图形;
(2)确定点的位置;
(3)确定直角三角形;
(4)分析直角三角形的边长,用勾股定理求解.
如图,是一个三级台阶,它的每一级的长、宽和高分别等于50cm,30cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
50
30
10
50
120
小试牛刀
例2 李叔叔想检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,随身只带了一把卷尺,
(1)你能替他想办法完成任务吗?
(2)量得AD长是30厘米,AB长是40厘米,BD长是50厘米。AD边垂直于AB边吗?
A
C
D
B
做一做
(3)如果李叔叔随身只有一个长度为20厘米的刻度尺,能有办法检验AD边是否垂直于AB边吗?边BC与边AB呢?
勾股定理与它的逆定理在应用上有什么区别?
议一议
勾股定理主要应用于在直角三角形中求线段
的长度,甚至周长或面积。
勾股定理的逆定理应用于根据三边的长度判断
三角形的形状。
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题,“今有池方一丈,葭生其中央,出水一尺。引葭赴岸,适与岸齐。问水深、葭长各几何?”这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?
试一试
中国人民的聪明智慧真的让人叹服!
5
解:设水池的深度为x尺,则芦苇的长度为 x+1尺。
x
x+1
由勾股定理得
x2 +52=(x+1)2
x=12
x2 +25= x2+2x+1
24= 2x
答:水池的深度为12尺,芦苇的长度为13尺
x+1=13(尺)
如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长。已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长
小试牛刀
交流小结
通过本节课的学习,我们学习了哪些知识内容?
1.勾股定理在实际生活中的应用;
2.数学思想:
转化
实际问题
小结
方程思想,数形结合思想
数学问题
用勾股定理解决实际问题的具体步骤:
1.审题,分析实际问题;
2.把实际问题转化为数学问题;
3.运用勾股定理计算;
4.检验是否符合实际问题的真实性。
作 业:
P14 习题1.4 第1,3,4题
课外思考题:
学而不思则惘
B
A
2.如果蚂蚁处于的位置是一个长、宽、高分别为5、4、3的长
方体的左下端A,它到右上端B的最短路线该怎样选择呢?
1. 八(9)班的学生想知道学校旗杆的高度,他们发现旗杆上的绳子垂到地面还多2米,如图(1),你能帮他们把旗杆的高度和绳子的长度计算出来吗?
感谢可爱的孩子们
再 见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
