北师大版八年级上册 2.7.2二次根式的运算 课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级上册 2.7.2二次根式的运算 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 23:22:01 | ||
图片预览







文档简介
(共21张PPT)
二次根式的运算
人教版
八年级
下册
学习目标
学习目标:
1.探索二次根式加减运算的方法和步骤;
2.会进行二次根式的加减运算.
学习重点:
1.在化简二次根式的基础上,应用分配律进行二次
根式的加减运算.
引入新课
5 dm
7.5 dm
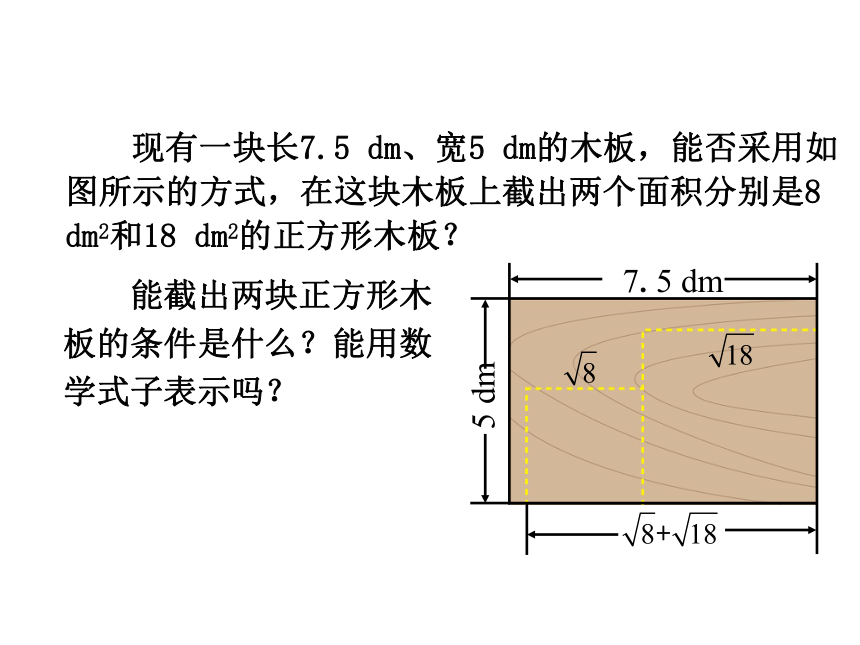
现有一块长7.5 dm、宽5 dm的木板,能否采用如图所示的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
讲授新课
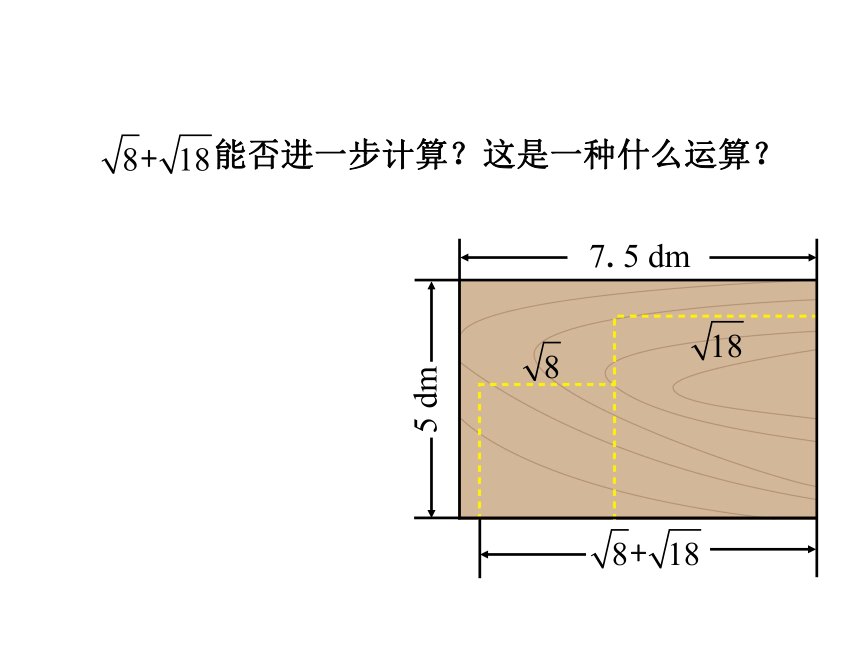
能否进一步计算?这是一种什么运算?
5 dm
7.5 dm
问题1
怎样计算 + ?
问题2:
有一个三角形它的两边长分别为 和 , 如果该三角形的周长为 ,你能求出第三边吗?
:
归纳:
1.如几个二次根式被开方数相同,可直接根据分配律进行加减运算。
2.如所给的二次根式不是最简单二次根式,应先化简,再考虑进行加减运算。
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫同类二次根式。
判断几个式子是不是同类二次根式的关键:
1.化成最简二次根式。
2.被开方数相同,根指头数相同。
1.在下列各组根式中,是同类二次根式的是( )
A B
C D
A
2.与 是同类二次根式的是( )
A B
C D
D
3.如果最简二次根式 与 是同类二次根式,求m,n的值。
例题解析
例1:下列各式中,哪些是同类二次根式?
注意:
判断是否为同类二次根式,只需看化为最简二次根式后被开方数是否相同,与最简二次根式前面的因式及符号无关。
例2:计算
(1) + - -
(2) + +
与合并同类项相类似,把同类二次根式
的系数相加减,做为结果的系数,根号及
根号内部都不变。
步骤:1.将每个二次根式化为最简二次根式
2.找出其中的同类二次根式。
3.合并同类二次根式。
“一化、二找、三合并”;
依据:
二次根式的性质、分配律和整式加减法则;
基本思想:
把二次根式加减问题转化为整式加减问题.
注意:不是同类二次根式不能合并。
请总结二次根式加减的步骤、依据和基本思想.
讲授新课
√
√
×
×
例1 判断下列计算是否正确?为什么?
(1)
(3)
(2)
(4)
讲授新课
计算下列各题,并注明每个步骤的依据:
化成最简
二次根式
合并被开方
数相同的二
次根式(即同类二次根式)
问题2:
讲授新课
课时小结
小结与收获:
(1)判断是否为同类二次根式的关键?
(2)二次根式的加减运算分哪几步进行?每一个步骤
的依据是什么?
二次根式的运算
人教版
八年级
下册
学习目标
学习目标:
1.探索二次根式加减运算的方法和步骤;
2.会进行二次根式的加减运算.
学习重点:
1.在化简二次根式的基础上,应用分配律进行二次
根式的加减运算.
引入新课
5 dm
7.5 dm
现有一块长7.5 dm、宽5 dm的木板,能否采用如图所示的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
能截出两块正方形木
板的条件是什么?能用数
学式子表示吗?
讲授新课
能否进一步计算?这是一种什么运算?
5 dm
7.5 dm
问题1
怎样计算 + ?
问题2:
有一个三角形它的两边长分别为 和 , 如果该三角形的周长为 ,你能求出第三边吗?
:
归纳:
1.如几个二次根式被开方数相同,可直接根据分配律进行加减运算。
2.如所给的二次根式不是最简单二次根式,应先化简,再考虑进行加减运算。
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式叫同类二次根式。
判断几个式子是不是同类二次根式的关键:
1.化成最简二次根式。
2.被开方数相同,根指头数相同。
1.在下列各组根式中,是同类二次根式的是( )
A B
C D
A
2.与 是同类二次根式的是( )
A B
C D
D
3.如果最简二次根式 与 是同类二次根式,求m,n的值。
例题解析
例1:下列各式中,哪些是同类二次根式?
注意:
判断是否为同类二次根式,只需看化为最简二次根式后被开方数是否相同,与最简二次根式前面的因式及符号无关。
例2:计算
(1) + - -
(2) + +
与合并同类项相类似,把同类二次根式
的系数相加减,做为结果的系数,根号及
根号内部都不变。
步骤:1.将每个二次根式化为最简二次根式
2.找出其中的同类二次根式。
3.合并同类二次根式。
“一化、二找、三合并”;
依据:
二次根式的性质、分配律和整式加减法则;
基本思想:
把二次根式加减问题转化为整式加减问题.
注意:不是同类二次根式不能合并。
请总结二次根式加减的步骤、依据和基本思想.
讲授新课
√
√
×
×
例1 判断下列计算是否正确?为什么?
(1)
(3)
(2)
(4)
讲授新课
计算下列各题,并注明每个步骤的依据:
化成最简
二次根式
合并被开方
数相同的二
次根式(即同类二次根式)
问题2:
讲授新课
课时小结
小结与收获:
(1)判断是否为同类二次根式的关键?
(2)二次根式的加减运算分哪几步进行?每一个步骤
的依据是什么?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
