2.5.2利用二次函数解一元二次方程 课件(共22张PPT)
文档属性
| 名称 | 2.5.2利用二次函数解一元二次方程 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 09:46:19 | ||
图片预览





文档简介
(共22张PPT)
2.5.2利用二次函数解一元二次方程
北师大版 九年级 下册
教学目标
教学目标:1. 利用二次函数的图象求一元二次方程的近似解.
2. 经历探索用二次函数图象求解一元二次方程近似解的过程,
体会用二次函数函数图象求一元二次方程解的方法.
教学重点:利用数形结合的思想估计一元二次方程近似解.
教学难点:用逼近法求一元二次方程近似解.
新知讲解
合作学习
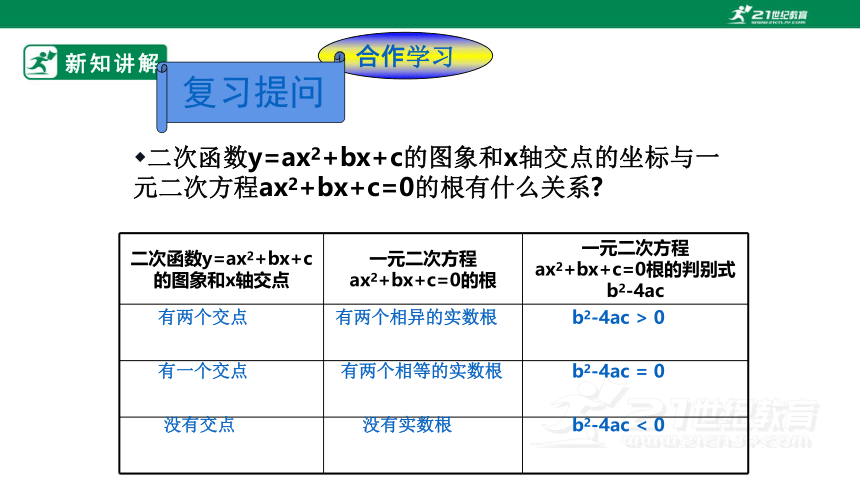
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
复习提问
合作学习
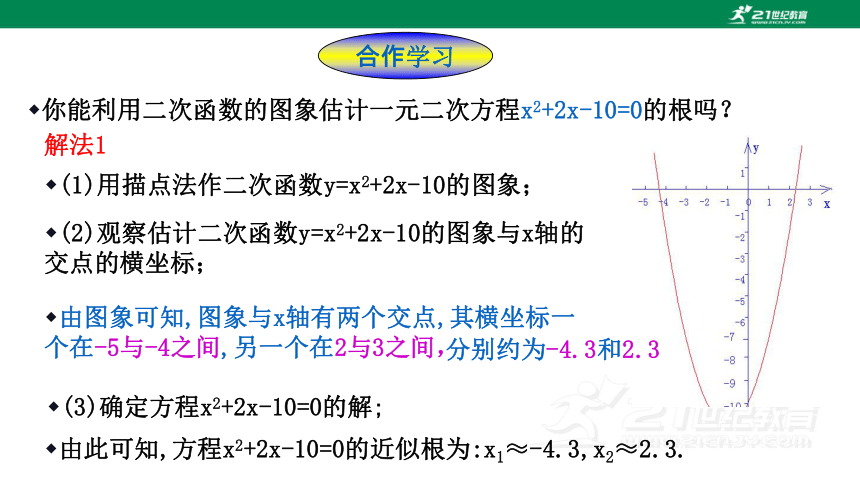
(1)用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2)观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,
(3)确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
分别约为-4.3和2.3
解法1
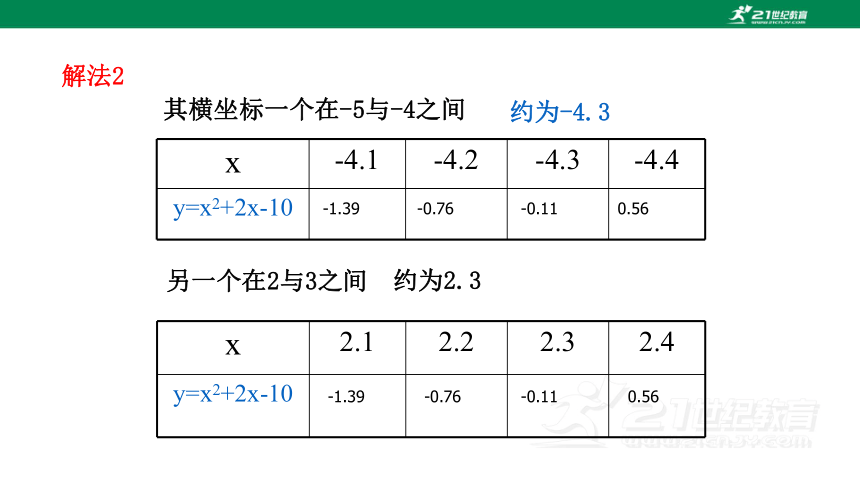
x -4.1 -4.2 -4.3 -4.4
y=x2+2x-10
x 2.1 2.2 2.3 2.4
y=x2+2x-10
其横坐标一个在-5与-4之间
另一个在2与3之间
约为-4.3
约为2.3
-1.39
-0.76
-0.11
0.56
-1.39
-0.76
-0.11
0.56
解法2
提炼概念
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解.
典例精讲
(1) 用描点法作二次函数y=x2+2x-10图象;
例:利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3) 观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
(2) 作直线y=3;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为
-4.7和2.7.
(4) 借助计算器确定方程x2+2x-10=3
的近似根为:x1≈-4.7,x2≈2.7.
(如何更准确估计近似值?)
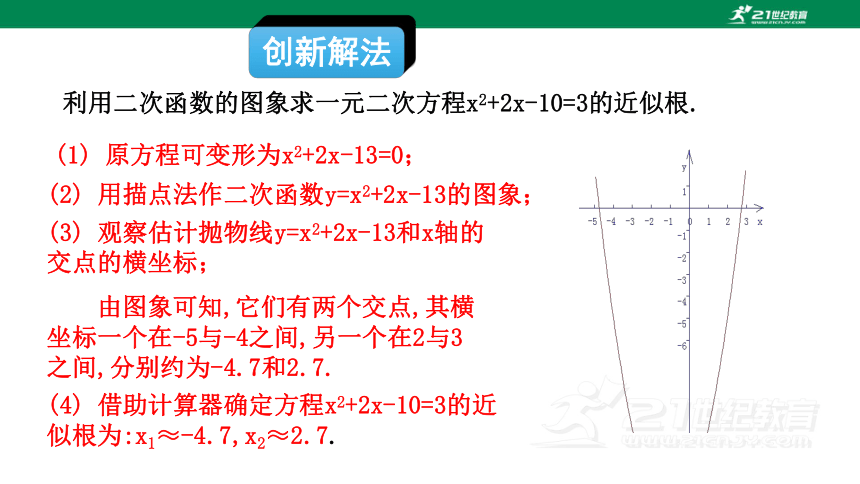
(1) 原方程可变形为x2+2x-13=0;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3) 观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7.
(4) 借助计算器确定方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2) 用描点法作二次函数y=x2+2x-13的图象;
创新解法
归纳概念
利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=h的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与直线y=h的交点的横坐标;
③确定一元二次方程ax2+bx+c=h的解.
课堂练习
C
1.
2.根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A.3C.3.24x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
D
4.二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
解:(1).观察估计二次函数y=-2x2+4x+1的图象与x轴的交点的横坐标;
(2)由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在2与3之间,分别约为-0.2和2.2(可将单位长再十等分,借助计算器确定其近似值).
(3).确定方程-2x2+4x+1=0的解;
由此可知,方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
5.利用二次函数的图象求一元二次方程3x2-x=1的近似根.
解:(1)用描点法作二次函数y=3x2-x-1的图象;
(2)观察估计二次函数y=3x2-x-1的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在0与1之间,分别约为-0.4和0.8.
(3)确定方程3x2-x-1=0的解;
方程3x2-x-1=0的近似根为:x1≈-0.4,x2≈0.8.
6.二次函数y=-x2+mx的图象如图,对称轴为直线x=2.若关于x的一元二次方程-x2+mx-t=0(t为实数)在1解:如图,关于x的一元二次方程-x2+mx-t=0的解就是抛物线
y=-x2+mx与直线y=t的交点的横坐标.
易得二次函数表达式为y=-x2+4x.
当x=1时,y=3;当x=5时,y=-5;当x=2时,y=4.
由图象可知,关于x的一元二次方程-x2+mx-t=0(t为实数)在1∴-5课堂总结
一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h(h是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.5.2利用二次函数解一元二次方程
北师大版 九年级 下册
教学目标
教学目标:1. 利用二次函数的图象求一元二次方程的近似解.
2. 经历探索用二次函数图象求解一元二次方程近似解的过程,
体会用二次函数函数图象求一元二次方程解的方法.
教学重点:利用数形结合的思想估计一元二次方程近似解.
教学难点:用逼近法求一元二次方程近似解.
新知讲解
合作学习
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
复习提问
合作学习
(1)用描点法作二次函数y=x2+2x-10的图象;
你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?
(2)观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,
(3)确定方程x2+2x-10=0的解;
由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.
分别约为-4.3和2.3
解法1
x -4.1 -4.2 -4.3 -4.4
y=x2+2x-10
x 2.1 2.2 2.3 2.4
y=x2+2x-10
其横坐标一个在-5与-4之间
另一个在2与3之间
约为-4.3
约为2.3
-1.39
-0.76
-0.11
0.56
-1.39
-0.76
-0.11
0.56
解法2
提炼概念
利用二次函数y=ax2+bx+c的图象求一元二次方
程ax2+bx+c=0的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与x轴的交点的横坐标;
③确定一元二次方程ax2+bx+c=0的解.
典例精讲
(1) 用描点法作二次函数y=x2+2x-10图象;
例:利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3) 观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;
(2) 作直线y=3;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为
-4.7和2.7.
(4) 借助计算器确定方程x2+2x-10=3
的近似根为:x1≈-4.7,x2≈2.7.
(如何更准确估计近似值?)
(1) 原方程可变形为x2+2x-13=0;
利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.
(3) 观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7.
(4) 借助计算器确定方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.
(2) 用描点法作二次函数y=x2+2x-13的图象;
创新解法
归纳概念
利用二次函数y=ax2+bx+c的图象求一元二次方程ax2+bx+c=h的近似根的一般步骤是怎样的?
①用描点法作二次函数y=ax2+bx+c的图象;
②观察估计二次函数的图象与直线y=h的交点的横坐标;
③确定一元二次方程ax2+bx+c=h的解.
课堂练习
C
1.
2.根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A.3
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
D
4.二次函数y=-2x2+4x+1的图象如图所示,求一元二次方程-2x2+4x+1=0的近似根.
解:(1).观察估计二次函数y=-2x2+4x+1的图象与x轴的交点的横坐标;
(2)由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在2与3之间,分别约为-0.2和2.2(可将单位长再十等分,借助计算器确定其近似值).
(3).确定方程-2x2+4x+1=0的解;
由此可知,方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.
5.利用二次函数的图象求一元二次方程3x2-x=1的近似根.
解:(1)用描点法作二次函数y=3x2-x-1的图象;
(2)观察估计二次函数y=3x2-x-1的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在0与1之间,分别约为-0.4和0.8.
(3)确定方程3x2-x-1=0的解;
方程3x2-x-1=0的近似根为:x1≈-0.4,x2≈0.8.
6.二次函数y=-x2+mx的图象如图,对称轴为直线x=2.若关于x的一元二次方程-x2+mx-t=0(t为实数)在1
y=-x2+mx与直线y=t的交点的横坐标.
易得二次函数表达式为y=-x2+4x.
当x=1时,y=3;当x=5时,y=-5;当x=2时,y=4.
由图象可知,关于x的一元二次方程-x2+mx-t=0(t为实数)在1
一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h(h是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
