2022-2023学年安徽省宿州市埇桥区教育集团八年级(上)期中数学试卷 (含解析)
文档属性
| 名称 | 2022-2023学年安徽省宿州市埇桥区教育集团八年级(上)期中数学试卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 10:16:50 | ||
图片预览



文档简介
2022-2023学年安徽省宿州市埇桥区教育集团八年级(上)期中数学试卷
一、选择题(每小题2分,共20分)
1.(2分)在0.458,,,,,这几个数中无理数有( )个.
A.1 B.2 C.3 D.4
2.(2分)下列长度的三条线段不能组成直角三角形的是( )
A.1.5,2.5,3 B.1,,2 C.6,8,10 D.5,12,13
3.(2分)若点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,点P的坐标是( )
A.(﹣4,3) B.(4,﹣3) C.(﹣3,4) D.(3,﹣4)
4.(2分)若点(m,n)在一次函数y=2x+1的图象上,则2m﹣n的值为( )
A.﹣2 B.﹣1 C.1 D.2
5.(2分)如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,1) C.(1,﹣2) D.(﹣3,1)
6.(2分)设边长为3的正方形的对角线长为a,下列关于a的说法错误的是( )
A.a是无理数
B.a可以用数轴上的一个点来表示
C.3<a<4
D.a是18的算术平方根
7.(2分)正比例函数y=kx的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
8.(2分)如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
9.(2分)将直线y=x+1向上平移5个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法错误的是( )
A.函数图象经过第一、二、三象限
B.函数图象与x轴的交点在x轴的正半轴
C.点(﹣2,4)在函数图象上
D.y随x的增大而增大
10.(2分)如图,一只蚂蚁沿着半圆形凹槽匀速爬行,则其顺着O→A→B→C→O运动的过程中,运动的时间x与蚂蚁离圆心的距离y之间的函数图象可大致表示为( )
A. B.
C. D.
二.填空题:(每小题3分,共18分)
11.(3分)9的算术平方根是 .
12.(3分)若点A(1﹣m,﹣1)与点B(2,1+n)关于y轴对称,则2m+n= .
13.(3分)写出一个y随x增大而减小的一次函数表达式,使它经过(﹣1,2).这个函数可以是 .
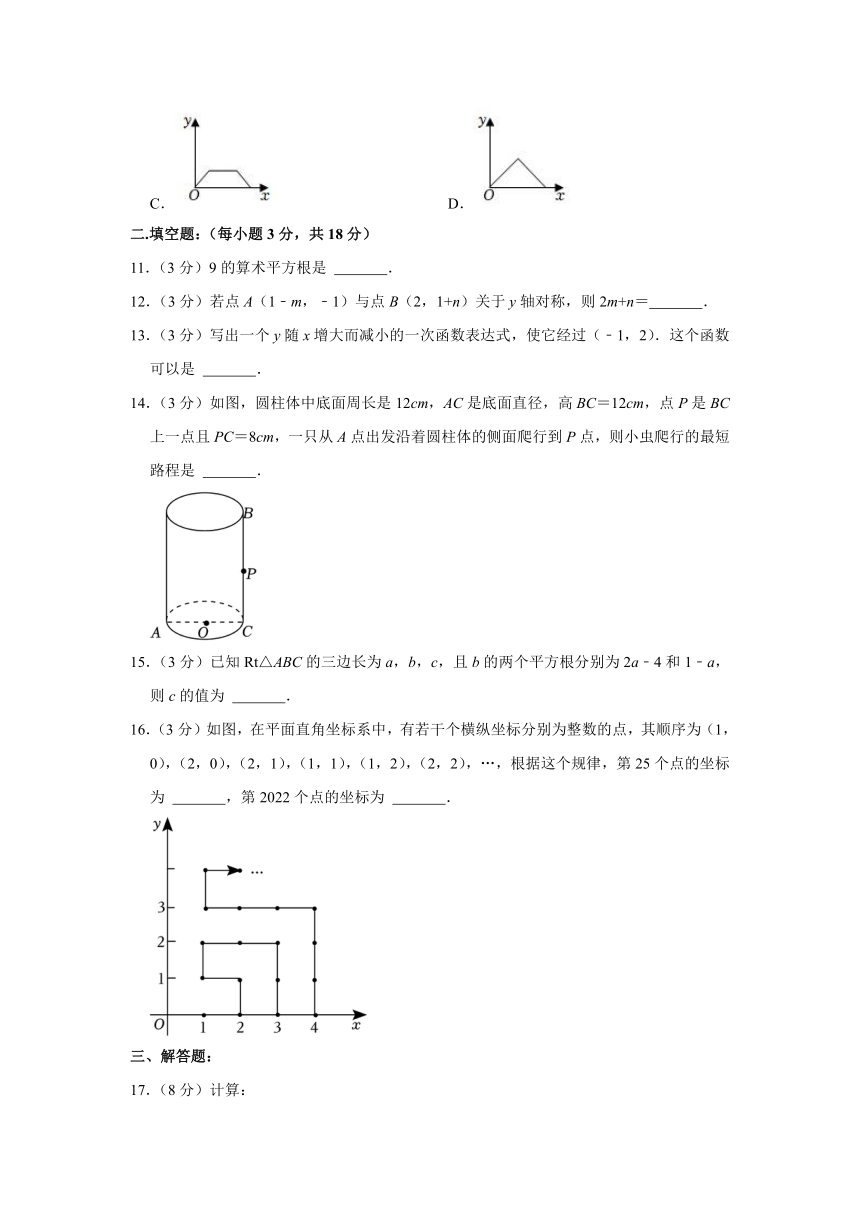
14.(3分)如图,圆柱体中底面周长是12cm,AC是底面直径,高BC=12cm,点P是BC上一点且PC=8cm,一只从A点出发沿着圆柱体的侧面爬行到P点,则小虫爬行的最短路程是 .
15.(3分)已知Rt△ABC的三边长为a,b,c,且b的两个平方根分别为2a﹣4和1﹣a,则c的值为 .
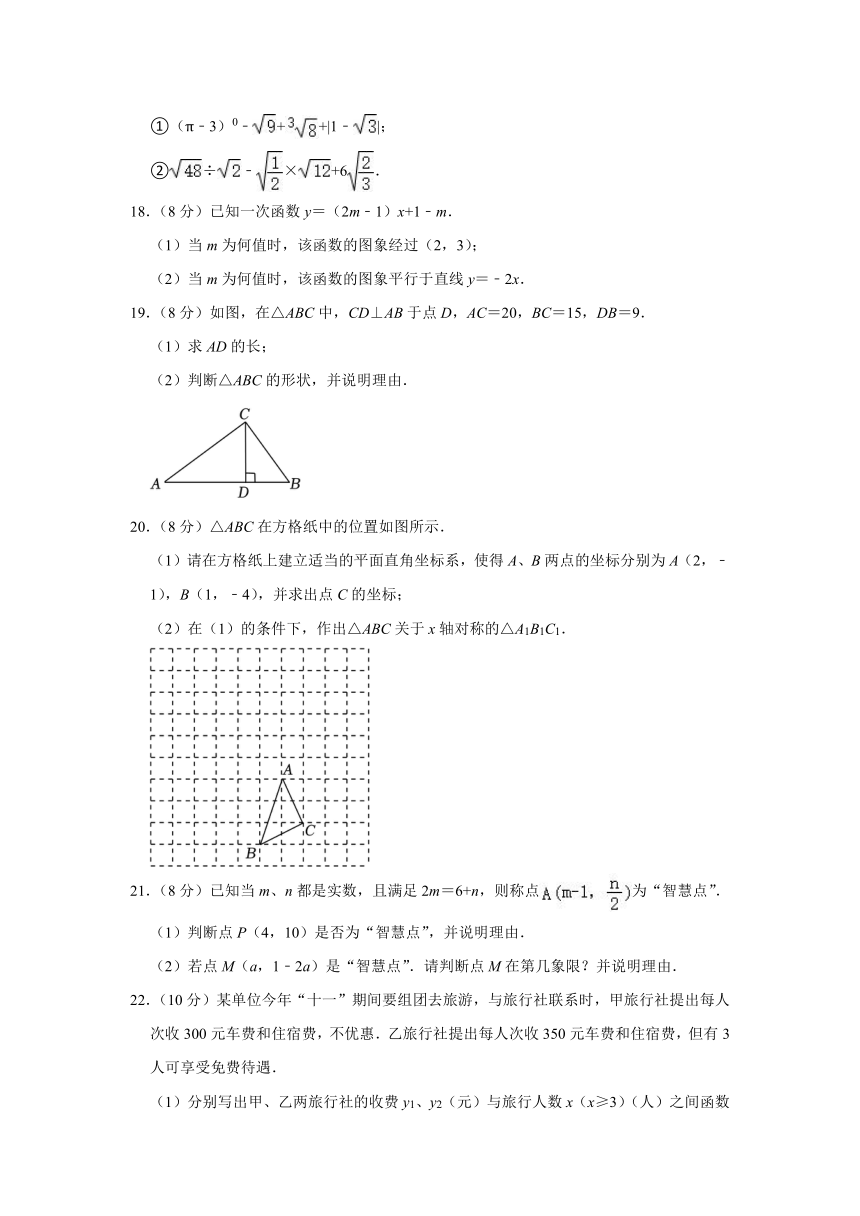
16.(3分)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 ,第2022个点的坐标为 .
三、解答题:
17.(8分)计算:
①(π﹣3)0﹣++|1﹣|;
②÷﹣×+6.
18.(8分)已知一次函数y=(2m﹣1)x+1﹣m.
(1)当m为何值时,该函数的图象经过(2,3);
(2)当m为何值时,该函数的图象平行于直线y=﹣2x.
19.(8分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求AD的长;
(2)判断△ABC的形状,并说明理由.
20.(8分)△ABC在方格纸中的位置如图所示.
(1)请在方格纸上建立适当的平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1),B(1,﹣4),并求出点C的坐标;
(2)在(1)的条件下,作出△ABC关于x轴对称的△A1B1C1.
21.(8分)已知当m、n都是实数,且满足2m=6+n,则称点为“智慧点”.
(1)判断点P(4,10)是否为“智慧点”,并说明理由.
(2)若点M(a,1﹣2a)是“智慧点”.请判断点M在第几象限?并说明理由.
22.(10分)某单位今年“十一”期间要组团去旅游,与旅行社联系时,甲旅行社提出每人次收300元车费和住宿费,不优惠.乙旅行社提出每人次收350元车费和住宿费,但有3人可享受免费待遇.
(1)分别写出甲、乙两旅行社的收费y1、y2(元)与旅行人数x(x≥3)(人)之间函数关系式;
(2)如果组织20人的旅行团时,选哪家旅行社比较合算?
(3)当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
23.(12分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,点C、D均在函数图象上.
(1)判断点是否在直线AB上,并说明理由;
(2)当﹣1≤y≤3时,求x的取值范围;
(3)在x轴上是否存在点P,使得△ADP的面积为3?若存在,请求出点P的坐标;若不存在,请说明理由.
2022-2023学年安徽省宿州市埇桥区教育集团八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题2分,共20分)
1.(2分)在0.458,,,,,这几个数中无理数有( )个.
A.1 B.2 C.3 D.4
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定求解即可.
【解答】解:∵
∴在0.458,,,,,这几个数中,
有理数有:0.458,,,,
无理数有,,共2个.
故选:B.
2.(2分)下列长度的三条线段不能组成直角三角形的是( )
A.1.5,2.5,3 B.1,,2 C.6,8,10 D.5,12,13
【分析】根据勾股定理的逆定理逐项判断即可.
【解答】解:A.1.52+2.52≠32,不能组成直角三角形,符合题意;
B. ,能组成直角三角形,不符合题意;
C.62+82=102,能组成直角三角形,不符合题意;
D.52+122=132,能组成直角三角形,不符合题意;
故选:A.
3.(2分)若点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,点P的坐标是( )
A.(﹣4,3) B.(4,﹣3) C.(﹣3,4) D.(3,﹣4)
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度结合第二象限内点的坐标特征解答.
【解答】解:∵点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,
∴点P的横坐标是﹣3,纵坐标是4,
∴点P的坐标为(﹣3,4).
故选:C.
4.(2分)若点(m,n)在一次函数y=2x+1的图象上,则2m﹣n的值为( )
A.﹣2 B.﹣1 C.1 D.2
【分析】利用一次函数图象上点的坐标特征可得出n=2m+1,变形后即可得出2m﹣n=﹣1.
【解答】解:∵点(m,n)在函数y=2x+1的图象上,
∴n=2m+1,
∴2m﹣n=﹣1.
故选:B.
5.(2分)如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,1) C.(1,﹣2) D.(﹣3,1)
【分析】根据“马”和“帅”的坐标建立出坐标系即可得到答案.
【解答】解:由题意建立坐标系,
∴“兵”位于点(﹣3,1).
故选:D.
6.(2分)设边长为3的正方形的对角线长为a,下列关于a的说法错误的是( )
A.a是无理数
B.a可以用数轴上的一个点来表示
C.3<a<4
D.a是18的算术平方根
【分析】根据勾股定理,可得a的长,根据a的长,可得答案.
【解答】解:a=,
Aa是无理数,故A正确;
B实数与数轴上的点一一对应,故B正确;
Ca>4,故C错误;
Da=,故D正确;
故选:C.
7.(2分)正比例函数y=kx的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
【分析】根据正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.
【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,
∴k<0,
∵一次函数y=x+k的一次项系数大于0,常数项小于0,
∴一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.
故选:A.
8.(2分)如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.
【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.
∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,
∴OA=OB=,
∴a=﹣1﹣.
故选:A.
9.(2分)将直线y=x+1向上平移5个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法错误的是( )
A.函数图象经过第一、二、三象限
B.函数图象与x轴的交点在x轴的正半轴
C.点(﹣2,4)在函数图象上
D.y随x的增大而增大
【分析】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.
【解答】解:将直线y=x+1向上平移5个单位长度后得到直线y=x+1+5,即y=x+6,
A、直线y=x+6经过第一、二、三象限,故不符合题意;
B、直线y=x+6与x轴交于(﹣6,0),即与x轴交于正半轴,故符合题意;
C、当x=﹣2时,y=﹣2+6=4,即点(﹣2,4)在函数图象上,故不符合题意;
D、直线y=x+6中,a=1>0,则y随x的增大而增大,故不符合题意.
故选:B.
10.(2分)如图,一只蚂蚁沿着半圆形凹槽匀速爬行,则其顺着O→A→B→C→O运动的过程中,运动的时间x与蚂蚁离圆心的距离y之间的函数图象可大致表示为( )
A. B.
C. D.
【分析】根据蚂蚁爬向A时距离O的距离越来越远,在上运动时,随着时间的变化,距离不发生变化,得出图象是与x轴平行的线段,从C爬向O时距离O的距离越来越小即可得出结论.
【解答】解:一只蚂蚁从O点出发,沿着半圆形凹槽匀速爬行,在开始时经过半径OA这一段,蚂蚁到O点的距离y随运动时间t的增大而增大;
到弧ABC这一段,蚂蚁到O点的距离y不变,图象是与x轴平行的线段;走另一条半径CO时,蚂蚁离圆心的距离y随t的增大而减小;
故选:C.
二.填空题:(每小题3分,共18分)
11.(3分)9的算术平方根是 3 .
【分析】9的平方根为±3,算术平方根为非负,从而得出结论.
【解答】解:∵(±3)2=9,
∴9的算术平方根是3.
故答案为:3.
12.(3分)若点A(1﹣m,﹣1)与点B(2,1+n)关于y轴对称,则2m+n= 4 .
【分析】根据点的坐标关于坐标轴对称“关于谁对称,谁就不变,另一个互为相反数”,进而问题可求解.
【解答】解:由题意得:1﹣m=﹣2,1+n=﹣1,
∴m=3,n=﹣2,
∴2m+n=2×3﹣2=4;
故答案为:4.
13.(3分)写出一个y随x增大而减小的一次函数表达式,使它经过(﹣1,2).这个函数可以是 y=﹣x+1(答案不唯一) .
【分析】设一次函数表达式为y=kx+b(k≠0),由y随x的增大而减小,利用一次函数的性质可得出k<0,取k=﹣1,结合一次函数图象经过点(﹣1,2)可得出b=1,进而可得出一次函数表达式可以为y=﹣x+1.
【解答】解:设一次函数表达式为y=kx+b(k≠0).
∵y随x的增大而减小,
∴k<0,取k=﹣1.
又∵一次函数图象经过点(﹣1,2),
∴1+b=2,解得b=1,
∴一次函数的表达式为y=﹣x+1.
故答案为:y=﹣x+1(答案不唯一).
14.(3分)如图,圆柱体中底面周长是12cm,AC是底面直径,高BC=12cm,点P是BC上一点且PC=8cm,一只从A点出发沿着圆柱体的侧面爬行到P点,则小虫爬行的最短路程是 10cm .
【分析】先把图形展开,连接AP,求出CP、AC长,根据勾股定理求出AP即可.
【解答】解:如图展开,连接AP,则线段AP的长是从A点出发沿着圆柱的表面爬行到点P的最短距离,
∵PC=8cm,
∵圆柱的底面周长为12cm,
∴AC=6cm,
在Rt△ACP中,由勾股定理得:AP==10(cm),
故答案为:10cm.
15.(3分)已知Rt△ABC的三边长为a,b,c,且b的两个平方根分别为2a﹣4和1﹣a,则c的值为 5或 .
【分析】根据平方根的性质可得2a﹣4+1﹣a=0,从而得到a=3,b=(1﹣a)2=4,然后分两种情况讨论:当c为斜边时,当c为直角边时,即可求解.
【解答】解:∵b的两个平方根分别为2a﹣4和1﹣a,
∴2a﹣4+1﹣a=0,
解得:a=3,
∴b=(1﹣a)2=4,
当c为斜边时,,
当c为直角边时,,
故答案为:5或.
16.(3分)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 (5,0) ,第2022个点的坐标为 (45,3) .
【分析】观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…,
右下角的点的横坐标为n时,共有n2个,
①∵52=25,5是奇数,
∴第25个点是(5,0),
②∵452=2025,45是奇数,
∴第2025个点是(45,0),
即第2022个点是(45,3)
故答案为(5,0),(45,3).
三、解答题:
17.(8分)计算:
①(π﹣3)0﹣++|1﹣|;
②÷﹣×+6.
【分析】①直接利用零指数幂的性质、立方根的性质、绝对值的性质、二次根式的性质分别化简,进而得出答案;
②直接利用二次根式的乘除运算法则化简,进而得出答案.
【解答】解:①(π﹣3)0﹣++|1﹣|
=1﹣3+2+﹣1
=﹣1+;
②÷﹣×+6
=2﹣+6×
=2﹣+2
=3.
18.(8分)已知一次函数y=(2m﹣1)x+1﹣m.
(1)当m为何值时,该函数的图象经过(2,3);
(2)当m为何值时,该函数的图象平行于直线y=﹣2x.
【分析】(1)将点的坐标代入解析式即可求出m的值;
(2)根据平行直线的比例系数相同解答.
【解答】解:(1)∵该函数的图象经过(2,3),
∴2(2m﹣1)+1﹣m=3,
解得,
答:当时,该函数的图象经过点(2,3);
(2)∵该函数的图象平行于直线y=﹣2x,
∴2m﹣1=﹣2,
解得 ,
答:当时,该函数的图象平行于直线y=﹣2x.
19.(8分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求AD的长;
(2)判断△ABC的形状,并说明理由.
【分析】(1)应用勾股定理,求出CD,再运用勾股定理即可求出AD;
(2)判断出AC2+BC2=AB2,即可判断△ABC为直角三角形.
【解答】解:(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,由勾股定理得:,
在Rt△BCD中,由勾股定理得,
(2)△ABC是直角三角形,
理由:由(1)知:AD=16,
∴AB=AD+DB=16+9=25,
在△ABC中,
∵AC2+BC2=202+152=625,AB2=252=625,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
20.(8分)△ABC在方格纸中的位置如图所示.
(1)请在方格纸上建立适当的平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1),B(1,﹣4),并求出点C的坐标;
(2)在(1)的条件下,作出△ABC关于x轴对称的△A1B1C1.
【分析】(1)由A、B两点坐标确定原点,再建立平面直角坐标系即可,由所建立的平面直角坐标系即可直接得出点C的坐标;
(2)找出△ABC各顶点关于x轴对称的对应点A1、B1、C1,再顺次连接A1、B1、C1即可.
【解答】解:(1)建立的平面直角坐标系如图所示,
∴点C的坐标为:(3,﹣3);
(2)如图,△A1B1C1即为所作.
21.(8分)已知当m、n都是实数,且满足2m=6+n,则称点为“智慧点”.
(1)判断点P(4,10)是否为“智慧点”,并说明理由.
(2)若点M(a,1﹣2a)是“智慧点”.请判断点M在第几象限?并说明理由.
【分析】(1)根据P点坐标,代入中,求出m和n的值,然后代入2m,6+n检验等号是否成立即可;
(2)直接利用“智慧点”的定义得出a的值进而得出答案.
【解答】解:(1)点P不是“智慧点”,
由题意得:,
∴m=5,n=20,
∴2m=2×5=10,
6+n=6+20=26,
∴2m≠6+n,
∴点P(4,10)不是“智慧点”;
(2)点M在第四象限,
理由:∵点M(a,1﹣2a)是“智慧点”,
∴,
∴m=a+1,n=2﹣4a,
∵2n=6+n,
∴2(a+1)=6+2﹣4a,
解得a=1,
∴点M(1,﹣1),
∴点M在第四象限.
22.(10分)某单位今年“十一”期间要组团去旅游,与旅行社联系时,甲旅行社提出每人次收300元车费和住宿费,不优惠.乙旅行社提出每人次收350元车费和住宿费,但有3人可享受免费待遇.
(1)分别写出甲、乙两旅行社的收费y1、y2(元)与旅行人数x(x≥3)(人)之间函数关系式;
(2)如果组织20人的旅行团时,选哪家旅行社比较合算?
(3)当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
【分析】(1)设甲旅行社的收费为y1元,乙旅行社的收费为y2元,旅行人数为x人,根据单价乘以数量等于总价就可以表示出y与x之间的函数关系式;
(2)将x=20分别代入y1与y2的解析式,求出y1与y2的大小,进行比较就可以求出结论;
(3)根据所需费用一样多列方程可解得答案.
【解答】解:(1)根据题意得:
y1=300x,
y2=350(x﹣3)=350x﹣1050.
答:y1=300x,y2=350x﹣1050(x≥3);
(2)当x=20时,
y1=300×20=6000元,
y2=350×20﹣1050=5950元;
∵6000>5950,
∴y1>y2,
∴选择乙旅行社比较合算;
(3)∵所需费用一样多,
∴300x=350(x﹣3),
解得x=21,
答:当旅行团为21人时,选甲或乙旅行社所需费用一样多.
23.(12分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,点C、D均在函数图象上.
(1)判断点是否在直线AB上,并说明理由;
(2)当﹣1≤y≤3时,求x的取值范围;
(3)在x轴上是否存在点P,使得△ADP的面积为3?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)在中,令得,即知,0)在直线AB上;
(2)在中,令y=﹣1得,得x=2,令y=3得,得x=﹣1,然后问题可求解;
(3)求出D,A的坐标,由△ADP的面积为3,可得,从而可得P的坐标.
【解答】解:(1),0)在直线AB上,理由如下:
在中,
令得,∴,0)在直线AB上;
(2)解:在中,
令y=﹣1得,
解得x=2,
令y=3得,
解得x=﹣1,∴当﹣1≤y≤3时,x的取值范围是﹣1≤x≤2;
(3)解:存在点P,
理由:由(1)知:点,由(2)知:点D(﹣1,3),
设点P的坐标为(m,0),
∴,
∵S△ADP=3,
∴,
解得,
综上所述,点P的坐标为或.
一、选择题(每小题2分,共20分)
1.(2分)在0.458,,,,,这几个数中无理数有( )个.
A.1 B.2 C.3 D.4
2.(2分)下列长度的三条线段不能组成直角三角形的是( )
A.1.5,2.5,3 B.1,,2 C.6,8,10 D.5,12,13
3.(2分)若点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,点P的坐标是( )
A.(﹣4,3) B.(4,﹣3) C.(﹣3,4) D.(3,﹣4)
4.(2分)若点(m,n)在一次函数y=2x+1的图象上,则2m﹣n的值为( )
A.﹣2 B.﹣1 C.1 D.2
5.(2分)如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,1) C.(1,﹣2) D.(﹣3,1)
6.(2分)设边长为3的正方形的对角线长为a,下列关于a的说法错误的是( )
A.a是无理数
B.a可以用数轴上的一个点来表示
C.3<a<4
D.a是18的算术平方根
7.(2分)正比例函数y=kx的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
8.(2分)如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
9.(2分)将直线y=x+1向上平移5个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法错误的是( )
A.函数图象经过第一、二、三象限
B.函数图象与x轴的交点在x轴的正半轴
C.点(﹣2,4)在函数图象上
D.y随x的增大而增大
10.(2分)如图,一只蚂蚁沿着半圆形凹槽匀速爬行,则其顺着O→A→B→C→O运动的过程中,运动的时间x与蚂蚁离圆心的距离y之间的函数图象可大致表示为( )
A. B.
C. D.
二.填空题:(每小题3分,共18分)
11.(3分)9的算术平方根是 .
12.(3分)若点A(1﹣m,﹣1)与点B(2,1+n)关于y轴对称,则2m+n= .
13.(3分)写出一个y随x增大而减小的一次函数表达式,使它经过(﹣1,2).这个函数可以是 .
14.(3分)如图,圆柱体中底面周长是12cm,AC是底面直径,高BC=12cm,点P是BC上一点且PC=8cm,一只从A点出发沿着圆柱体的侧面爬行到P点,则小虫爬行的最短路程是 .
15.(3分)已知Rt△ABC的三边长为a,b,c,且b的两个平方根分别为2a﹣4和1﹣a,则c的值为 .
16.(3分)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 ,第2022个点的坐标为 .
三、解答题:
17.(8分)计算:
①(π﹣3)0﹣++|1﹣|;
②÷﹣×+6.
18.(8分)已知一次函数y=(2m﹣1)x+1﹣m.
(1)当m为何值时,该函数的图象经过(2,3);
(2)当m为何值时,该函数的图象平行于直线y=﹣2x.
19.(8分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求AD的长;
(2)判断△ABC的形状,并说明理由.
20.(8分)△ABC在方格纸中的位置如图所示.
(1)请在方格纸上建立适当的平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1),B(1,﹣4),并求出点C的坐标;
(2)在(1)的条件下,作出△ABC关于x轴对称的△A1B1C1.
21.(8分)已知当m、n都是实数,且满足2m=6+n,则称点为“智慧点”.
(1)判断点P(4,10)是否为“智慧点”,并说明理由.
(2)若点M(a,1﹣2a)是“智慧点”.请判断点M在第几象限?并说明理由.
22.(10分)某单位今年“十一”期间要组团去旅游,与旅行社联系时,甲旅行社提出每人次收300元车费和住宿费,不优惠.乙旅行社提出每人次收350元车费和住宿费,但有3人可享受免费待遇.
(1)分别写出甲、乙两旅行社的收费y1、y2(元)与旅行人数x(x≥3)(人)之间函数关系式;
(2)如果组织20人的旅行团时,选哪家旅行社比较合算?
(3)当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
23.(12分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,点C、D均在函数图象上.
(1)判断点是否在直线AB上,并说明理由;
(2)当﹣1≤y≤3时,求x的取值范围;
(3)在x轴上是否存在点P,使得△ADP的面积为3?若存在,请求出点P的坐标;若不存在,请说明理由.
2022-2023学年安徽省宿州市埇桥区教育集团八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每小题2分,共20分)
1.(2分)在0.458,,,,,这几个数中无理数有( )个.
A.1 B.2 C.3 D.4
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定求解即可.
【解答】解:∵
∴在0.458,,,,,这几个数中,
有理数有:0.458,,,,
无理数有,,共2个.
故选:B.
2.(2分)下列长度的三条线段不能组成直角三角形的是( )
A.1.5,2.5,3 B.1,,2 C.6,8,10 D.5,12,13
【分析】根据勾股定理的逆定理逐项判断即可.
【解答】解:A.1.52+2.52≠32,不能组成直角三角形,符合题意;
B. ,能组成直角三角形,不符合题意;
C.62+82=102,能组成直角三角形,不符合题意;
D.52+122=132,能组成直角三角形,不符合题意;
故选:A.
3.(2分)若点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,点P的坐标是( )
A.(﹣4,3) B.(4,﹣3) C.(﹣3,4) D.(3,﹣4)
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度结合第二象限内点的坐标特征解答.
【解答】解:∵点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,
∴点P的横坐标是﹣3,纵坐标是4,
∴点P的坐标为(﹣3,4).
故选:C.
4.(2分)若点(m,n)在一次函数y=2x+1的图象上,则2m﹣n的值为( )
A.﹣2 B.﹣1 C.1 D.2
【分析】利用一次函数图象上点的坐标特征可得出n=2m+1,变形后即可得出2m﹣n=﹣1.
【解答】解:∵点(m,n)在函数y=2x+1的图象上,
∴n=2m+1,
∴2m﹣n=﹣1.
故选:B.
5.(2分)如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,1) C.(1,﹣2) D.(﹣3,1)
【分析】根据“马”和“帅”的坐标建立出坐标系即可得到答案.
【解答】解:由题意建立坐标系,
∴“兵”位于点(﹣3,1).
故选:D.
6.(2分)设边长为3的正方形的对角线长为a,下列关于a的说法错误的是( )
A.a是无理数
B.a可以用数轴上的一个点来表示
C.3<a<4
D.a是18的算术平方根
【分析】根据勾股定理,可得a的长,根据a的长,可得答案.
【解答】解:a=,
Aa是无理数,故A正确;
B实数与数轴上的点一一对应,故B正确;
Ca>4,故C错误;
Da=,故D正确;
故选:C.
7.(2分)正比例函数y=kx的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
【分析】根据正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.
【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,
∴k<0,
∵一次函数y=x+k的一次项系数大于0,常数项小于0,
∴一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.
故选:A.
8.(2分)如图所示,在数轴上点A所表示的数为a,则a的值为( )
A.﹣1﹣ B.1﹣ C.﹣ D.﹣1+
【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.
【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.
∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,
∴OA=OB=,
∴a=﹣1﹣.
故选:A.
9.(2分)将直线y=x+1向上平移5个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法错误的是( )
A.函数图象经过第一、二、三象限
B.函数图象与x轴的交点在x轴的正半轴
C.点(﹣2,4)在函数图象上
D.y随x的增大而增大
【分析】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.
【解答】解:将直线y=x+1向上平移5个单位长度后得到直线y=x+1+5,即y=x+6,
A、直线y=x+6经过第一、二、三象限,故不符合题意;
B、直线y=x+6与x轴交于(﹣6,0),即与x轴交于正半轴,故符合题意;
C、当x=﹣2时,y=﹣2+6=4,即点(﹣2,4)在函数图象上,故不符合题意;
D、直线y=x+6中,a=1>0,则y随x的增大而增大,故不符合题意.
故选:B.
10.(2分)如图,一只蚂蚁沿着半圆形凹槽匀速爬行,则其顺着O→A→B→C→O运动的过程中,运动的时间x与蚂蚁离圆心的距离y之间的函数图象可大致表示为( )
A. B.
C. D.
【分析】根据蚂蚁爬向A时距离O的距离越来越远,在上运动时,随着时间的变化,距离不发生变化,得出图象是与x轴平行的线段,从C爬向O时距离O的距离越来越小即可得出结论.
【解答】解:一只蚂蚁从O点出发,沿着半圆形凹槽匀速爬行,在开始时经过半径OA这一段,蚂蚁到O点的距离y随运动时间t的增大而增大;
到弧ABC这一段,蚂蚁到O点的距离y不变,图象是与x轴平行的线段;走另一条半径CO时,蚂蚁离圆心的距离y随t的增大而减小;
故选:C.
二.填空题:(每小题3分,共18分)
11.(3分)9的算术平方根是 3 .
【分析】9的平方根为±3,算术平方根为非负,从而得出结论.
【解答】解:∵(±3)2=9,
∴9的算术平方根是3.
故答案为:3.
12.(3分)若点A(1﹣m,﹣1)与点B(2,1+n)关于y轴对称,则2m+n= 4 .
【分析】根据点的坐标关于坐标轴对称“关于谁对称,谁就不变,另一个互为相反数”,进而问题可求解.
【解答】解:由题意得:1﹣m=﹣2,1+n=﹣1,
∴m=3,n=﹣2,
∴2m+n=2×3﹣2=4;
故答案为:4.
13.(3分)写出一个y随x增大而减小的一次函数表达式,使它经过(﹣1,2).这个函数可以是 y=﹣x+1(答案不唯一) .
【分析】设一次函数表达式为y=kx+b(k≠0),由y随x的增大而减小,利用一次函数的性质可得出k<0,取k=﹣1,结合一次函数图象经过点(﹣1,2)可得出b=1,进而可得出一次函数表达式可以为y=﹣x+1.
【解答】解:设一次函数表达式为y=kx+b(k≠0).
∵y随x的增大而减小,
∴k<0,取k=﹣1.
又∵一次函数图象经过点(﹣1,2),
∴1+b=2,解得b=1,
∴一次函数的表达式为y=﹣x+1.
故答案为:y=﹣x+1(答案不唯一).
14.(3分)如图,圆柱体中底面周长是12cm,AC是底面直径,高BC=12cm,点P是BC上一点且PC=8cm,一只从A点出发沿着圆柱体的侧面爬行到P点,则小虫爬行的最短路程是 10cm .
【分析】先把图形展开,连接AP,求出CP、AC长,根据勾股定理求出AP即可.
【解答】解:如图展开,连接AP,则线段AP的长是从A点出发沿着圆柱的表面爬行到点P的最短距离,
∵PC=8cm,
∵圆柱的底面周长为12cm,
∴AC=6cm,
在Rt△ACP中,由勾股定理得:AP==10(cm),
故答案为:10cm.
15.(3分)已知Rt△ABC的三边长为a,b,c,且b的两个平方根分别为2a﹣4和1﹣a,则c的值为 5或 .
【分析】根据平方根的性质可得2a﹣4+1﹣a=0,从而得到a=3,b=(1﹣a)2=4,然后分两种情况讨论:当c为斜边时,当c为直角边时,即可求解.
【解答】解:∵b的两个平方根分别为2a﹣4和1﹣a,
∴2a﹣4+1﹣a=0,
解得:a=3,
∴b=(1﹣a)2=4,
当c为斜边时,,
当c为直角边时,,
故答案为:5或.
16.(3分)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 (5,0) ,第2022个点的坐标为 (45,3) .
【分析】观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…,
右下角的点的横坐标为n时,共有n2个,
①∵52=25,5是奇数,
∴第25个点是(5,0),
②∵452=2025,45是奇数,
∴第2025个点是(45,0),
即第2022个点是(45,3)
故答案为(5,0),(45,3).
三、解答题:
17.(8分)计算:
①(π﹣3)0﹣++|1﹣|;
②÷﹣×+6.
【分析】①直接利用零指数幂的性质、立方根的性质、绝对值的性质、二次根式的性质分别化简,进而得出答案;
②直接利用二次根式的乘除运算法则化简,进而得出答案.
【解答】解:①(π﹣3)0﹣++|1﹣|
=1﹣3+2+﹣1
=﹣1+;
②÷﹣×+6
=2﹣+6×
=2﹣+2
=3.
18.(8分)已知一次函数y=(2m﹣1)x+1﹣m.
(1)当m为何值时,该函数的图象经过(2,3);
(2)当m为何值时,该函数的图象平行于直线y=﹣2x.
【分析】(1)将点的坐标代入解析式即可求出m的值;
(2)根据平行直线的比例系数相同解答.
【解答】解:(1)∵该函数的图象经过(2,3),
∴2(2m﹣1)+1﹣m=3,
解得,
答:当时,该函数的图象经过点(2,3);
(2)∵该函数的图象平行于直线y=﹣2x,
∴2m﹣1=﹣2,
解得 ,
答:当时,该函数的图象平行于直线y=﹣2x.
19.(8分)如图,在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9.
(1)求AD的长;
(2)判断△ABC的形状,并说明理由.
【分析】(1)应用勾股定理,求出CD,再运用勾股定理即可求出AD;
(2)判断出AC2+BC2=AB2,即可判断△ABC为直角三角形.
【解答】解:(1)∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,由勾股定理得:,
在Rt△BCD中,由勾股定理得,
(2)△ABC是直角三角形,
理由:由(1)知:AD=16,
∴AB=AD+DB=16+9=25,
在△ABC中,
∵AC2+BC2=202+152=625,AB2=252=625,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
20.(8分)△ABC在方格纸中的位置如图所示.
(1)请在方格纸上建立适当的平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1),B(1,﹣4),并求出点C的坐标;
(2)在(1)的条件下,作出△ABC关于x轴对称的△A1B1C1.
【分析】(1)由A、B两点坐标确定原点,再建立平面直角坐标系即可,由所建立的平面直角坐标系即可直接得出点C的坐标;
(2)找出△ABC各顶点关于x轴对称的对应点A1、B1、C1,再顺次连接A1、B1、C1即可.
【解答】解:(1)建立的平面直角坐标系如图所示,
∴点C的坐标为:(3,﹣3);
(2)如图,△A1B1C1即为所作.
21.(8分)已知当m、n都是实数,且满足2m=6+n,则称点为“智慧点”.
(1)判断点P(4,10)是否为“智慧点”,并说明理由.
(2)若点M(a,1﹣2a)是“智慧点”.请判断点M在第几象限?并说明理由.
【分析】(1)根据P点坐标,代入中,求出m和n的值,然后代入2m,6+n检验等号是否成立即可;
(2)直接利用“智慧点”的定义得出a的值进而得出答案.
【解答】解:(1)点P不是“智慧点”,
由题意得:,
∴m=5,n=20,
∴2m=2×5=10,
6+n=6+20=26,
∴2m≠6+n,
∴点P(4,10)不是“智慧点”;
(2)点M在第四象限,
理由:∵点M(a,1﹣2a)是“智慧点”,
∴,
∴m=a+1,n=2﹣4a,
∵2n=6+n,
∴2(a+1)=6+2﹣4a,
解得a=1,
∴点M(1,﹣1),
∴点M在第四象限.
22.(10分)某单位今年“十一”期间要组团去旅游,与旅行社联系时,甲旅行社提出每人次收300元车费和住宿费,不优惠.乙旅行社提出每人次收350元车费和住宿费,但有3人可享受免费待遇.
(1)分别写出甲、乙两旅行社的收费y1、y2(元)与旅行人数x(x≥3)(人)之间函数关系式;
(2)如果组织20人的旅行团时,选哪家旅行社比较合算?
(3)当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
【分析】(1)设甲旅行社的收费为y1元,乙旅行社的收费为y2元,旅行人数为x人,根据单价乘以数量等于总价就可以表示出y与x之间的函数关系式;
(2)将x=20分别代入y1与y2的解析式,求出y1与y2的大小,进行比较就可以求出结论;
(3)根据所需费用一样多列方程可解得答案.
【解答】解:(1)根据题意得:
y1=300x,
y2=350(x﹣3)=350x﹣1050.
答:y1=300x,y2=350x﹣1050(x≥3);
(2)当x=20时,
y1=300×20=6000元,
y2=350×20﹣1050=5950元;
∵6000>5950,
∴y1>y2,
∴选择乙旅行社比较合算;
(3)∵所需费用一样多,
∴300x=350(x﹣3),
解得x=21,
答:当旅行团为21人时,选甲或乙旅行社所需费用一样多.
23.(12分)如图,已知一次函数的图象与x轴、y轴分别交于点A、B,点C、D均在函数图象上.
(1)判断点是否在直线AB上,并说明理由;
(2)当﹣1≤y≤3时,求x的取值范围;
(3)在x轴上是否存在点P,使得△ADP的面积为3?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)在中,令得,即知,0)在直线AB上;
(2)在中,令y=﹣1得,得x=2,令y=3得,得x=﹣1,然后问题可求解;
(3)求出D,A的坐标,由△ADP的面积为3,可得,从而可得P的坐标.
【解答】解:(1),0)在直线AB上,理由如下:
在中,
令得,∴,0)在直线AB上;
(2)解:在中,
令y=﹣1得,
解得x=2,
令y=3得,
解得x=﹣1,∴当﹣1≤y≤3时,x的取值范围是﹣1≤x≤2;
(3)解:存在点P,
理由:由(1)知:点,由(2)知:点D(﹣1,3),
设点P的坐标为(m,0),
∴,
∵S△ADP=3,
∴,
解得,
综上所述,点P的坐标为或.
同课章节目录
