27.3位似(第一课时)位似图形的概念及画法
文档属性
| 名称 | 27.3位似(第一课时)位似图形的概念及画法 |  | |
| 格式 | zip | ||
| 文件大小 | 476.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-19 22:17:26 | ||
图片预览




文档简介
课件19张PPT。27.3 位 似27.3位似(第一课时)位似图形的概念及画法1. 前面我们已经学习了图形的哪些变换?平移:平移的方向,平移的距离.
旋转:旋转中心,旋转方向,旋转角度.
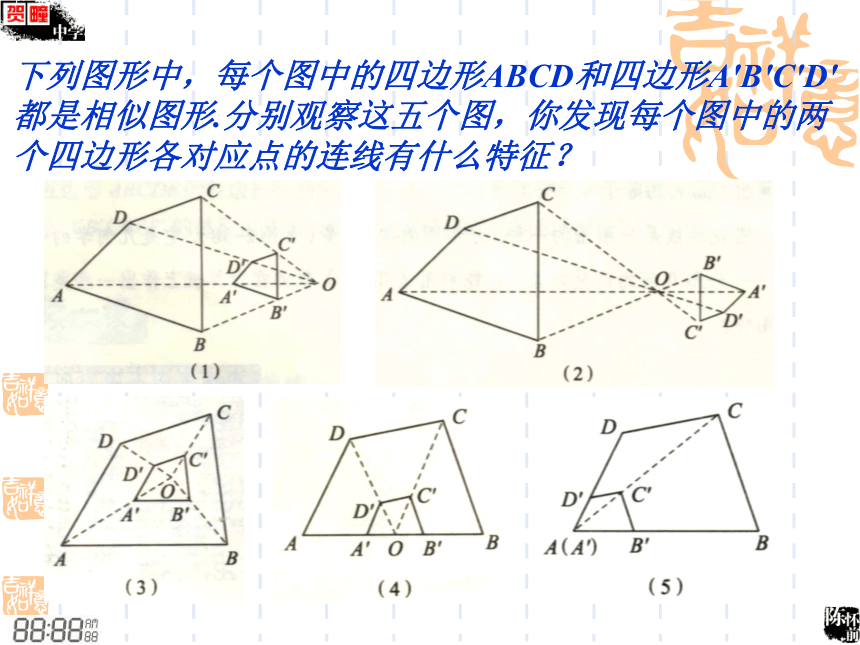
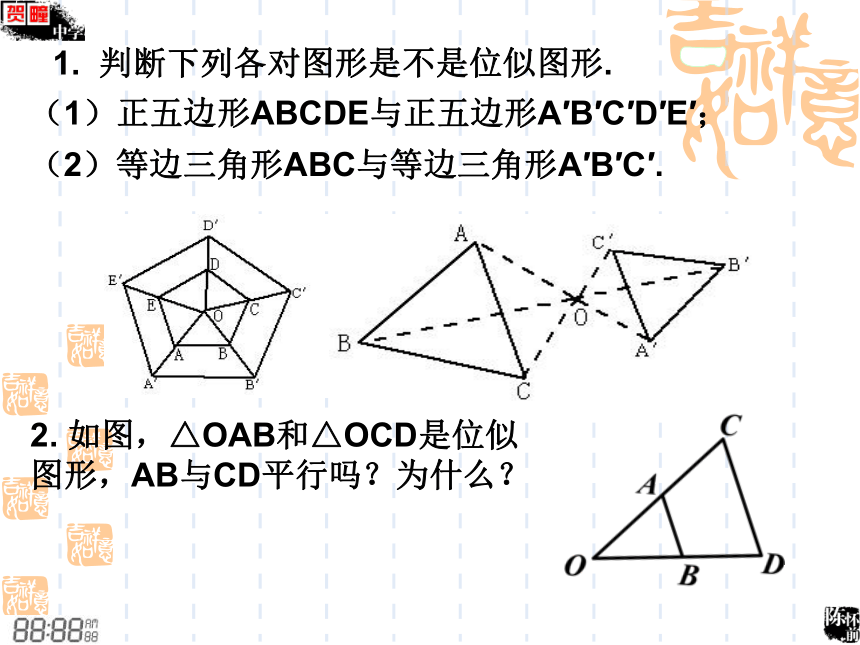
相似:相似比.对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.下面请欣赏如下图形的变换下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?1.位似图形的概念如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行(或在同一直线上),那么这样的两个图形叫做位似图形,这个点叫做位似中心.相似对应点的连线相交一点对应边平行(或在同一直线上)位似三要素1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; (2)等边三角形ABC与等边三角形A′B′C′.2. 如图,△OAB和△OCD是位似
图形,AB与CD平行吗?为什么?3. 如图所示的图形中,是位似图形的是________4. 如图,已知△EFH和△MNK是位似图形,那么其位似中心是点( ).判断下面的正方形是不是位似图形?(1)不是ACDBFEG显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形 位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。思考:位似图形有何性质?若△ABC与△A'B'C'的相似比为:1:2,
则OA:OA'=( )。OAA'BCB'C'1:2性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. O.ABCA'C'B'. 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍. OA:OA'=OB:OB'=OC:OC'= 1:2思考:还有没其他作法?OABA'C’B’CACBO如果位似中心跑到三角形内部呢?ABA’C’B’CO以0为中心把△ABC
缩小为原来的一半。 位似的作用 位似可以将一个图形放大或缩小。作位似图形,要用尺规作图
若指定位似中心,一般可作两个,位于位似中心两侧;
若不指定位似中心,一般可作无数个.①确定位似中心,位似中心的位置可随意选择;
②找到原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③在连线上取关键点的对应点,使之满足放缩比例;
④顺次连接截取对应点。 作位似的步骤 ①定 ②找 ③截 ④连1.位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
2.位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.
3.位似图形的作法:
①定 ②找 ③截 ④连课本P60 【习题27.3】第1、2、4题《名校课堂》P43~44
旋转:旋转中心,旋转方向,旋转角度.
相似:相似比.对称(轴对称与轴对称图形,中心对称与中心对称图形):对称轴,对称中心.注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.下面请欣赏如下图形的变换下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?1.位似图形的概念如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行(或在同一直线上),那么这样的两个图形叫做位似图形,这个点叫做位似中心.相似对应点的连线相交一点对应边平行(或在同一直线上)位似三要素1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; (2)等边三角形ABC与等边三角形A′B′C′.2. 如图,△OAB和△OCD是位似
图形,AB与CD平行吗?为什么?3. 如图所示的图形中,是位似图形的是________4. 如图,已知△EFH和△MNK是位似图形,那么其位似中心是点( ).判断下面的正方形是不是位似图形?(1)不是ACDBFEG显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形 位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。思考:位似图形有何性质?若△ABC与△A'B'C'的相似比为:1:2,
则OA:OA'=( )。OAA'BCB'C'1:2性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比. O.ABCA'C'B'. 1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍. OA:OA'=OB:OB'=OC:OC'= 1:2思考:还有没其他作法?OABA'C’B’CACBO如果位似中心跑到三角形内部呢?ABA’C’B’CO以0为中心把△ABC
缩小为原来的一半。 位似的作用 位似可以将一个图形放大或缩小。作位似图形,要用尺规作图
若指定位似中心,一般可作两个,位于位似中心两侧;
若不指定位似中心,一般可作无数个.①确定位似中心,位似中心的位置可随意选择;
②找到原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③在连线上取关键点的对应点,使之满足放缩比例;
④顺次连接截取对应点。 作位似的步骤 ①定 ②找 ③截 ④连1.位似图形的概念:
如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
2.位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.
3.位似图形的作法:
①定 ②找 ③截 ④连课本P60 【习题27.3】第1、2、4题《名校课堂》P43~44
