3.1.3空间向量数量积运算和+3.1.4空间向量的正交分解及其坐标表示 课件(共25张PPT)
文档属性
| 名称 | 3.1.3空间向量数量积运算和+3.1.4空间向量的正交分解及其坐标表示 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 659.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 13:11:58 | ||
图片预览








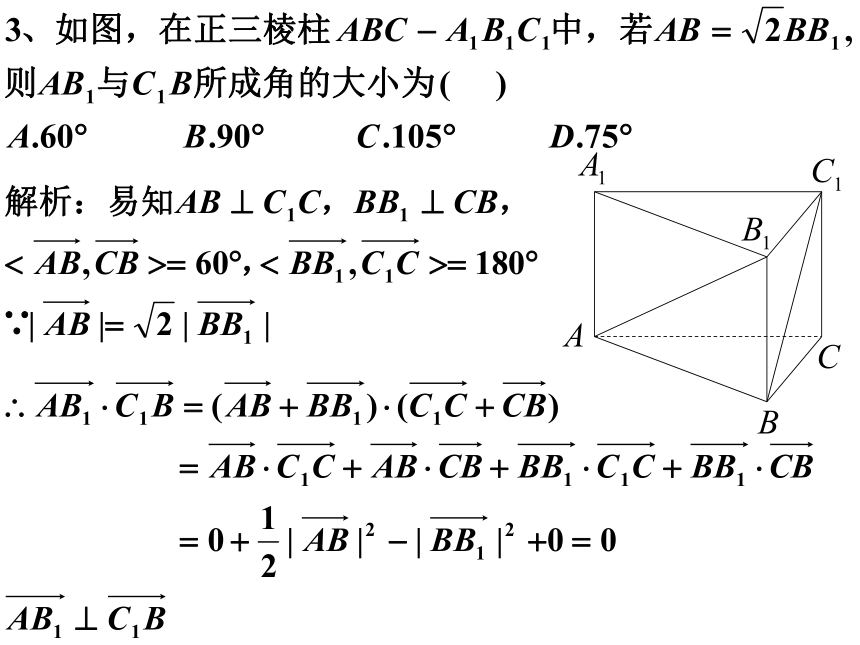
文档简介
(共25张PPT)
3.1.3 空间向量的数量积运算
3.1.4空间向量的
正交分解及其坐标表示
3.1.3 空间向量的数量积运算
一、复习回顾:平面向量的数量积运算
1、平面向量的数量积定义:
2、平面向量的数量积的几何意义:
3、平面向量的数量积的主要性质:
1)两个向量的夹角的定义:
a
O
A
b
B
二、类似地,我们可以定义空间向量的数量积运算:
2)空间向量的数量积
注:
①两个向量的数量积是数量,可以正,负或0,而不是向量.
②规定:零向量与任意向量的数量积为0.
a
O
A
b
B
C
思考:
3)空间两个向量的数量积性质
——数量积为零是判定两非零向量垂直的充要条件
——用于计算向量的模
——用于计算向量的夹角
4)空间向量的数量积满足的运算律
三、课堂练习
1350
变式1
5、已知线段AB、BD在平面a内,BD⊥AB,线段AC⊥a,如果AB=a,BD=b,AC=c,求C、D之间的距离.
解:∵
四.空间向量数量积在立体几何中的应用:
l
A
O
P
例2、已知m,n是平面 内的两条相交直线,直线l与m,n的交点为B,且l⊥m,l⊥n,求证:l⊥
m
n
B
g
l
五.拓展练习:
1、已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB
A
B
C
O
3.1.4空间向量的
正交分解及其坐标表示
A
课前练习
A′
B′
O
A
B
C
P
a
P′
新课讲解
O
A
B
C
P
a
P′
新课讲解
1、空间向量基本定理
注意:
新课讲解
1、空间向量基本定理
已知向量 是空间的一个基底,
试判断 构成该空间的另一个基底?
方程无解
假设 共面,则存在实数x,y使得
所以 不共面,可以作为一个基底
练习:
O
x
y
z
新课讲解
O
x
y
z
新课讲解
×
×
√
设正方体的棱长为2,如图,以D为原点建立空间直角坐标系,则向量 的坐标分别是什么?
练习1:
x
z
y
A'
B
C
A
D'
C'
B'
D
x
y
z
O
3.1.3 空间向量的数量积运算
3.1.4空间向量的
正交分解及其坐标表示
3.1.3 空间向量的数量积运算
一、复习回顾:平面向量的数量积运算
1、平面向量的数量积定义:
2、平面向量的数量积的几何意义:
3、平面向量的数量积的主要性质:
1)两个向量的夹角的定义:
a
O
A
b
B
二、类似地,我们可以定义空间向量的数量积运算:
2)空间向量的数量积
注:
①两个向量的数量积是数量,可以正,负或0,而不是向量.
②规定:零向量与任意向量的数量积为0.
a
O
A
b
B
C
思考:
3)空间两个向量的数量积性质
——数量积为零是判定两非零向量垂直的充要条件
——用于计算向量的模
——用于计算向量的夹角
4)空间向量的数量积满足的运算律
三、课堂练习
1350
变式1
5、已知线段AB、BD在平面a内,BD⊥AB,线段AC⊥a,如果AB=a,BD=b,AC=c,求C、D之间的距离.
解:∵
四.空间向量数量积在立体几何中的应用:
l
A
O
P
例2、已知m,n是平面 内的两条相交直线,直线l与m,n的交点为B,且l⊥m,l⊥n,求证:l⊥
m
n
B
g
l
五.拓展练习:
1、已知:在空间四边形OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB
A
B
C
O
3.1.4空间向量的
正交分解及其坐标表示
A
课前练习
A′
B′
O
A
B
C
P
a
P′
新课讲解
O
A
B
C
P
a
P′
新课讲解
1、空间向量基本定理
注意:
新课讲解
1、空间向量基本定理
已知向量 是空间的一个基底,
试判断 构成该空间的另一个基底?
方程无解
假设 共面,则存在实数x,y使得
所以 不共面,可以作为一个基底
练习:
O
x
y
z
新课讲解
O
x
y
z
新课讲解
×
×
√
设正方体的棱长为2,如图,以D为原点建立空间直角坐标系,则向量 的坐标分别是什么?
练习1:
x
z
y
A'
B
C
A
D'
C'
B'
D
x
y
z
O
