3.2.2-3.2.3空间向量的平行和垂直问题 课件(24张PPT)
文档属性
| 名称 | 3.2.2-3.2.3空间向量的平行和垂直问题 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 13:12:24 | ||
图片预览





文档简介
(共24张PPT)
3.2.2-3.2.3
空间向量的平行和垂直问题
A
平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.
给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的.
几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面的法向量,向量 是与平面平行或在平面内,则有
l
m
l
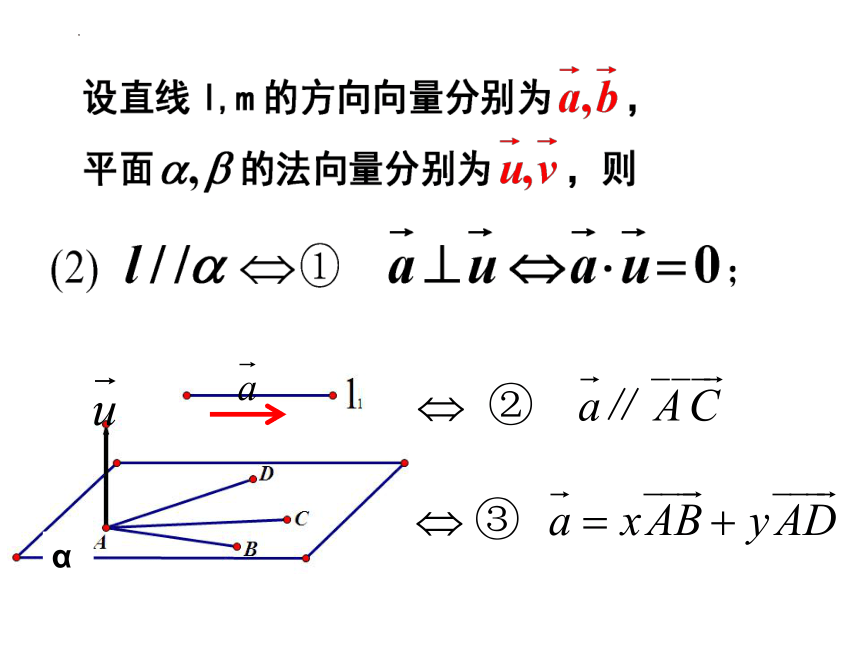
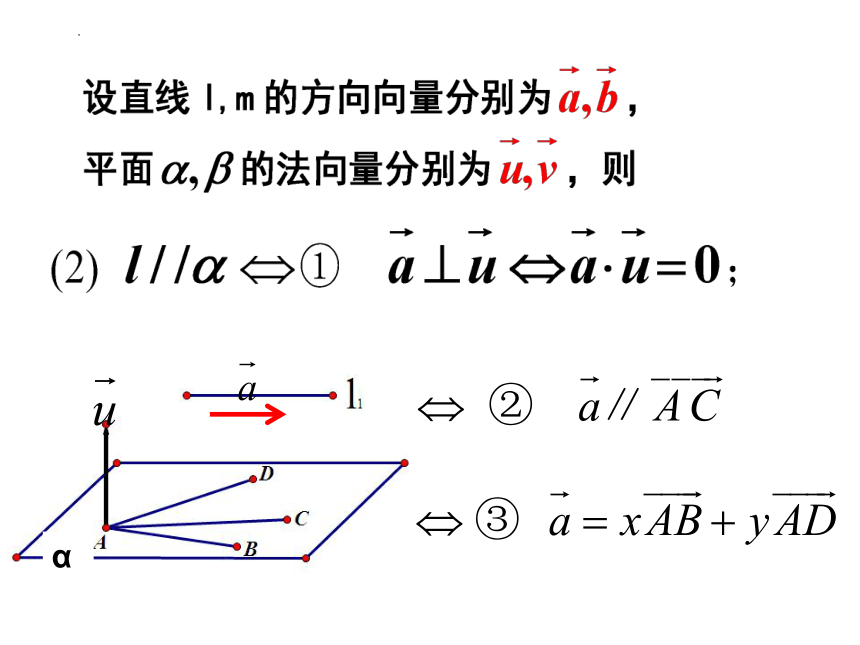
(一). 平行关系:
α
α
β
m
l
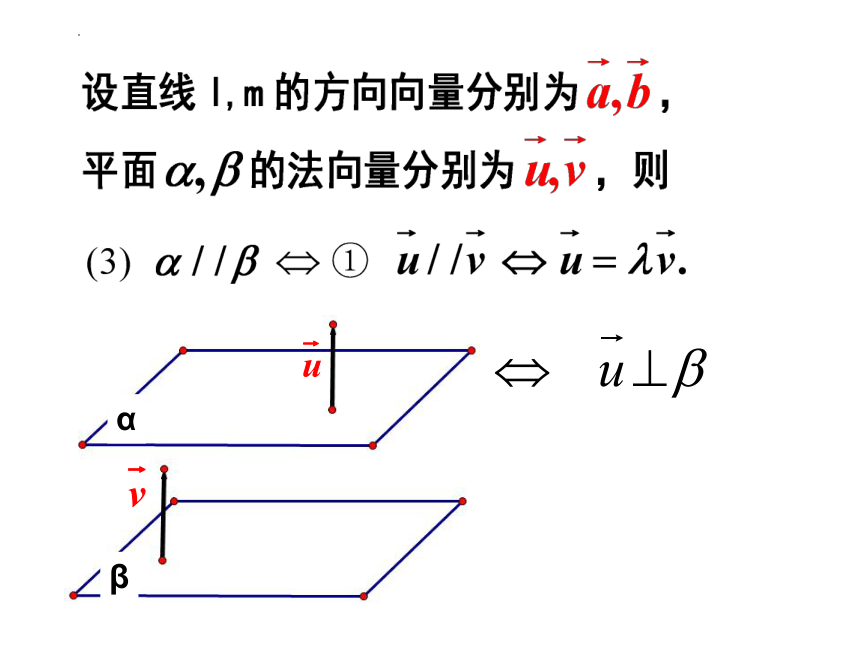
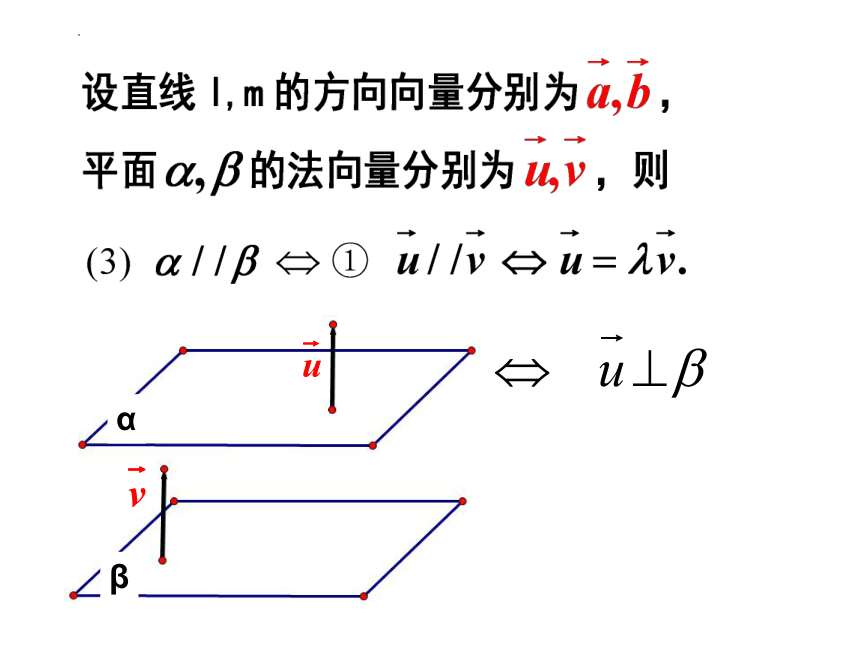
(一). 平行关系:
α
α
β
(二)、垂直关系:
l
m
l
A
B
C
α
β
1、平行关系:
2、垂直关系:
例1.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.
平行或重合
垂直
平行或重合
例1.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.
垂直
平行或重合
相交
例2 四棱锥P-ABCD中,底面ABCD是正方形, PD⊥底面ABCD,PD=DC=6, E是PB的中点,DF:FB=CG:GP=1:2 . 求证:AE//FG.
A
B
C
D
P
G
X
Y
Z
F
E
A(6,0,0),
F(2,2,0),
E(3,3,3),
G(0,4,2),
AE//FG
证 :如图所示, 建立空间直
角坐标系.
//
AE与FG不共线
几何法呢?
例3 四棱锥P-ABCD中,底面ABCD是正
方形,PD⊥底面ABCD,PD=DC, E是PC的
中点, (1)求证:PA//平面EDB.
A
B
C
D
P
E
X
Y
Z
G
解1 立体几何法
A
B
C
D
P
E
X
Y
Z
G
如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:连结AC,AC交BD于点G,连结EG
解法2
A
B
C
D
P
E
X
Y
Z
解3:如图所示建立空间直角坐标系,
点D为坐标原点,设DC=1
(1)证明:
设平面EDB的法向量为
A
B
C
D
P
E
X
Y
Z
解4:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:
解得 x=-2,y=1
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
是BB1,,CD中点,求证:D1F
例4 正方体
中,E、F分别
平面ADE.
证明:设正方体棱长为1, 为单位正交基底,建立如图所示坐标系D-xyz,
所以
,E是AA1中点,
例5 正方体
平面C1BD.
证明:
E
求证:平面EBD
设正方体棱长为2, 建立如图所示坐标系
平面C1BD的一个法向量是
E(0,0,1)
D(0,2,0)
B(2,0,0)
设平面EBD的一个法向量是
平面C1BD.
平面EBD
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
CD中点,求证:D1F
练习.在正方体
中,E、F分别是BB1,,
平面ADE
所以
3.2.2-3.2.3
空间向量的平行和垂直问题
A
平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量.
给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的.
几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面的法向量,向量 是与平面平行或在平面内,则有
l
m
l
(一). 平行关系:
α
α
β
m
l
(一). 平行关系:
α
α
β
(二)、垂直关系:
l
m
l
A
B
C
α
β
1、平行关系:
2、垂直关系:
例1.设 分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.
平行或重合
垂直
平行或重合
例1.设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.
垂直
平行或重合
相交
例2 四棱锥P-ABCD中,底面ABCD是正方形, PD⊥底面ABCD,PD=DC=6, E是PB的中点,DF:FB=CG:GP=1:2 . 求证:AE//FG.
A
B
C
D
P
G
X
Y
Z
F
E
A(6,0,0),
F(2,2,0),
E(3,3,3),
G(0,4,2),
AE//FG
证 :如图所示, 建立空间直
角坐标系.
//
AE与FG不共线
几何法呢?
例3 四棱锥P-ABCD中,底面ABCD是正
方形,PD⊥底面ABCD,PD=DC, E是PC的
中点, (1)求证:PA//平面EDB.
A
B
C
D
P
E
X
Y
Z
G
解1 立体几何法
A
B
C
D
P
E
X
Y
Z
G
如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:连结AC,AC交BD于点G,连结EG
解法2
A
B
C
D
P
E
X
Y
Z
解3:如图所示建立空间直角坐标系,
点D为坐标原点,设DC=1
(1)证明:
设平面EDB的法向量为
A
B
C
D
P
E
X
Y
Z
解4:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1
(1)证明:
解得 x=-2,y=1
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
是BB1,,CD中点,求证:D1F
例4 正方体
中,E、F分别
平面ADE.
证明:设正方体棱长为1, 为单位正交基底,建立如图所示坐标系D-xyz,
所以
,E是AA1中点,
例5 正方体
平面C1BD.
证明:
E
求证:平面EBD
设正方体棱长为2, 建立如图所示坐标系
平面C1BD的一个法向量是
E(0,0,1)
D(0,2,0)
B(2,0,0)
设平面EBD的一个法向量是
平面C1BD.
平面EBD
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
CD中点,求证:D1F
练习.在正方体
中,E、F分别是BB1,,
平面ADE
所以
