3.1.5 空间向量运算的坐标表示 课件(12张PPT)
文档属性
| 名称 | 3.1.5 空间向量运算的坐标表示 课件(12张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 13:45:02 | ||
图片预览


文档简介
(共12张PPT)
3.1.5 空间向量的坐标运算
z
x
O
y
飞机的飞行速度是很快的,时速都在1 000 km以上,全世界的飞机非常多,这些飞机在天空中风驰电掣,速度是如此的快,不是很容易撞机吗?我们如何确定一架飞机在空中的位置呢?
复习旧知一:空间直角坐标系
一、空间直角坐标系
y
z
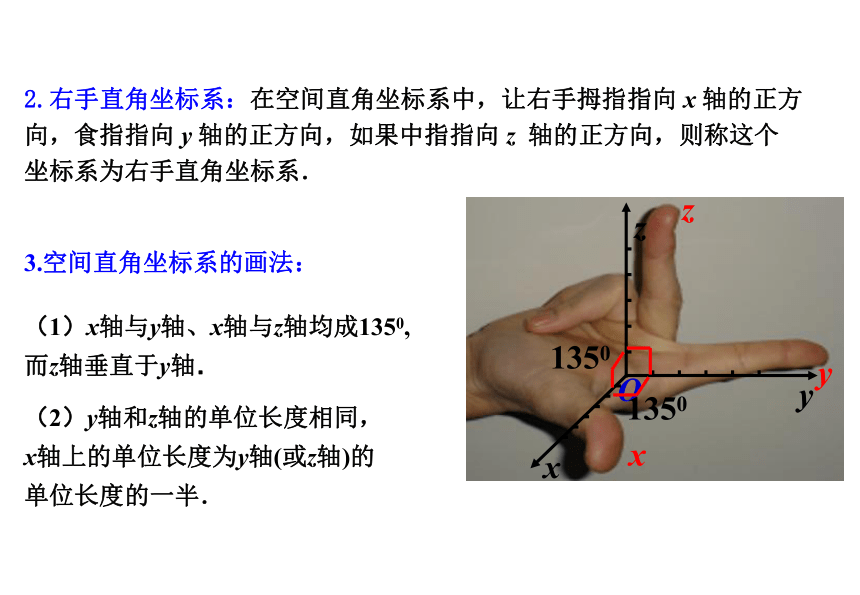
如图, 是单位正方体.以O为原点,分别以射线OA,OC,OD’ 的方向为正方向,以线段OA,OC, OD’的长为单位长,建立三条数轴:x轴、y 轴、z 轴.这时我们说建立了一个空间直角坐标系 ,
A
B
C
O
x
1.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
其中点O 叫做坐标原点,
x轴、y 轴、z 轴叫做坐标轴.
2.右手直角坐标系:在空间直角坐标系中,让右手拇指指向 x 轴的正方向,食指指向 y 轴的正方向,如果中指指向 z 轴的正方向,则称这个坐标系为右手直角坐标系.
x
y
z
(1)x轴与y轴、x轴与z轴均成1350,而z轴垂直于y轴.
(2)y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半.
3.空间直角坐标系的画法:
O
x
y
z
1350
1350
二、空间点的坐标
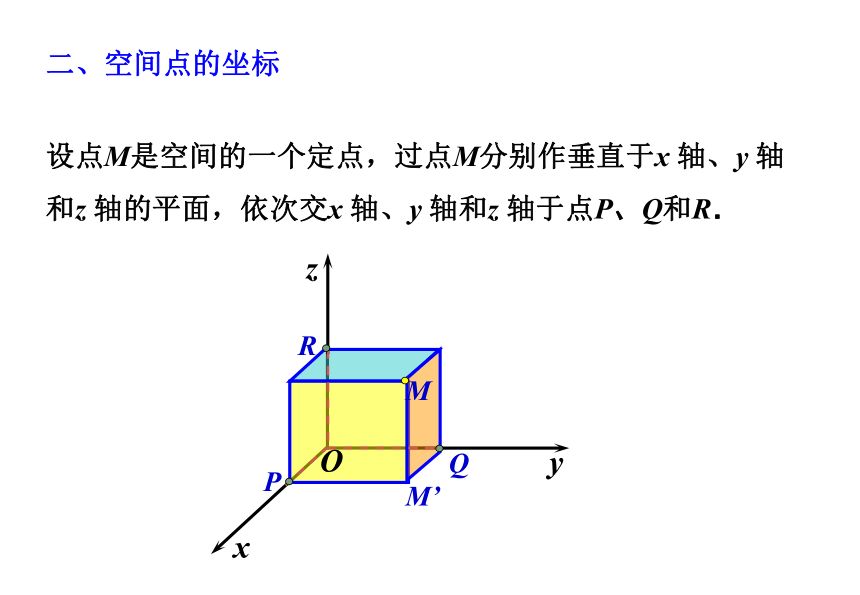
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
y
x
z
M’
O
M
R
Q
P
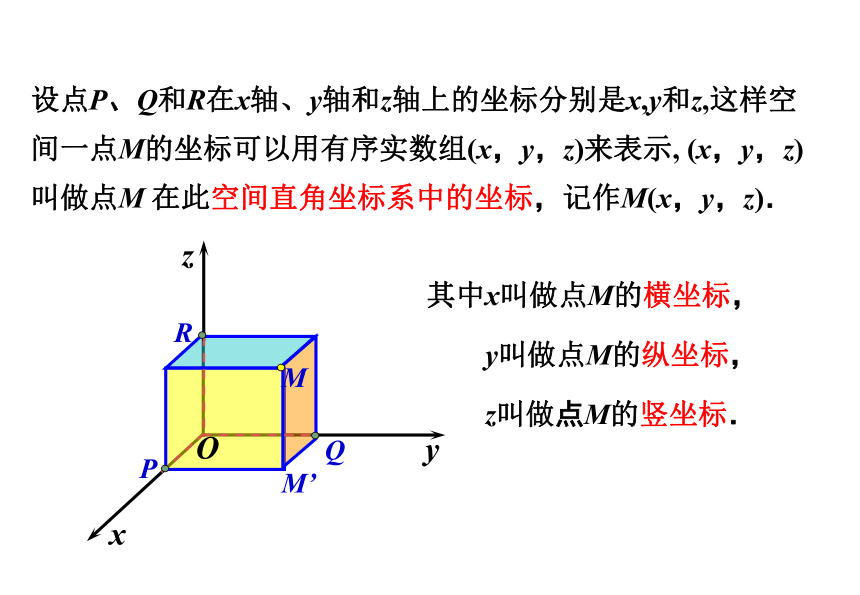
设点P、Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,这样空间一点M的坐标可以用有序实数组(x,y,z)来表示, (x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).
其中x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.
y
x
z
M’
O
M
R
Q
P
复习二 平面向量的坐标运算
1.空间向量a,b,其坐标形式为a=(a1,a2),b=(b1,b2).
向量运算 向量表示 坐标表示
加法 a+b a+b=_______________________
减法 a-b a-b=_______________________
数乘 λa λa=_______________
数量积 a·b a·b=________________
(a1+b1,a2+b2,)
(a1-b1,a2-b2,)
(λa1,λa2,)
a1b1+a2b2
2. 平面向量的平行、垂直及模、夹角
设a=(a1,a2),b=(b1,b2),则
名称 满足条件 向量表示形式 坐标表示形式
a∥b a=λb(λ∈R) a1=λb1,a2=λb2(λ∈R)
a⊥b a·b=0 a·b=___________________
模 |a|=______ ___________________
夹角 cos〈a,b〉= cos〈a,b〉=
a1b1+a2b2=0
新课讲解: 类比平面向量,探求空间向量的坐标运算
一、空间向量a,b,其坐标形式为a=(a1,a2,a3),b=(b1,b2,b3).
向量运算 向量表示 坐标表示
加法 a+b a+b=_______________________
减法 a-b a-b=_______________________
数乘 λa λa=_______________
数量积 a·b a·b=________________
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
知识点二 空间向量的平行、垂直及模、夹角
设a=(a1,a2,a3),b=(b1,b2,b3),则
名称 满足条件 向量表示形式 坐标表示形式
a∥b a=λb(λ∈R) a1=λb1,a2=λb2,a3=λb3(λ∈R)
a⊥b a·b=0 a·b=___________________
模 |a|=______ ___________________
夹角 cos〈a,b〉= cos〈a,b〉=
a1b1+a2b2+a3b3=0
知识点三 向量的坐标及两点间的距离公式
在空间直角坐标系中,设A(a1,b1,c1),B(a2,b2,c2),则
(1) = ;
(2)dAB= = .
(a2-a1,b2-b1,c2-c1)
课后作业
1、 活页61-62《3.1.5空间向量运算的坐标表示》
3.1.5 空间向量的坐标运算
z
x
O
y
飞机的飞行速度是很快的,时速都在1 000 km以上,全世界的飞机非常多,这些飞机在天空中风驰电掣,速度是如此的快,不是很容易撞机吗?我们如何确定一架飞机在空中的位置呢?
复习旧知一:空间直角坐标系
一、空间直角坐标系
y
z
如图, 是单位正方体.以O为原点,分别以射线OA,OC,OD’ 的方向为正方向,以线段OA,OC, OD’的长为单位长,建立三条数轴:x轴、y 轴、z 轴.这时我们说建立了一个空间直角坐标系 ,
A
B
C
O
x
1.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
其中点O 叫做坐标原点,
x轴、y 轴、z 轴叫做坐标轴.
2.右手直角坐标系:在空间直角坐标系中,让右手拇指指向 x 轴的正方向,食指指向 y 轴的正方向,如果中指指向 z 轴的正方向,则称这个坐标系为右手直角坐标系.
x
y
z
(1)x轴与y轴、x轴与z轴均成1350,而z轴垂直于y轴.
(2)y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半.
3.空间直角坐标系的画法:
O
x
y
z
1350
1350
二、空间点的坐标
设点M是空间的一个定点,过点M分别作垂直于x 轴、y 轴和z 轴的平面,依次交x 轴、y 轴和z 轴于点P、Q和R.
y
x
z
M’
O
M
R
Q
P
设点P、Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,这样空间一点M的坐标可以用有序实数组(x,y,z)来表示, (x,y,z)叫做点M 在此空间直角坐标系中的坐标,记作M(x,y,z).
其中x叫做点M的横坐标,
y叫做点M的纵坐标,
z叫做点M的竖坐标.
y
x
z
M’
O
M
R
Q
P
复习二 平面向量的坐标运算
1.空间向量a,b,其坐标形式为a=(a1,a2),b=(b1,b2).
向量运算 向量表示 坐标表示
加法 a+b a+b=_______________________
减法 a-b a-b=_______________________
数乘 λa λa=_______________
数量积 a·b a·b=________________
(a1+b1,a2+b2,)
(a1-b1,a2-b2,)
(λa1,λa2,)
a1b1+a2b2
2. 平面向量的平行、垂直及模、夹角
设a=(a1,a2),b=(b1,b2),则
名称 满足条件 向量表示形式 坐标表示形式
a∥b a=λb(λ∈R) a1=λb1,a2=λb2(λ∈R)
a⊥b a·b=0 a·b=___________________
模 |a|=______ ___________________
夹角 cos〈a,b〉= cos〈a,b〉=
a1b1+a2b2=0
新课讲解: 类比平面向量,探求空间向量的坐标运算
一、空间向量a,b,其坐标形式为a=(a1,a2,a3),b=(b1,b2,b3).
向量运算 向量表示 坐标表示
加法 a+b a+b=_______________________
减法 a-b a-b=_______________________
数乘 λa λa=_______________
数量积 a·b a·b=________________
(a1+b1,a2+b2,a3+b3)
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
知识点二 空间向量的平行、垂直及模、夹角
设a=(a1,a2,a3),b=(b1,b2,b3),则
名称 满足条件 向量表示形式 坐标表示形式
a∥b a=λb(λ∈R) a1=λb1,a2=λb2,a3=λb3(λ∈R)
a⊥b a·b=0 a·b=___________________
模 |a|=______ ___________________
夹角 cos〈a,b〉= cos〈a,b〉=
a1b1+a2b2+a3b3=0
知识点三 向量的坐标及两点间的距离公式
在空间直角坐标系中,设A(a1,b1,c1),B(a2,b2,c2),则
(1) = ;
(2)dAB= = .
(a2-a1,b2-b1,c2-c1)
课后作业
1、 活页61-62《3.1.5空间向量运算的坐标表示》
