2.1.2 演绎推理 课件(16张PPT)
文档属性
| 名称 | 2.1.2 演绎推理 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 13:14:20 | ||
图片预览




文档简介
(共16张PPT)
2.1.2 演绎推理
北京师范大学银川学校
2.1.2 演绎推理
2、合情推理的思维过程
合情推理
归纳推理
类比推理
1、合情推理的分类
复习回顾
一般原理 特殊情况 结论
所有金属都能导电 铜是金属
太阳系大行星以椭圆轨道绕太阳运行 天王星是太阳系的大行星
奇数都不能被2整除 2017是奇数
三角函数都是周期函数 因为三角函数
铜能导电
天王星以椭圆形轨道绕太阳运行
2017不能被2整除
所以是周期函数
观察发现
思考1:观察上述推理具有怎样的特征?
思考2:每一个例子由几部分组成?
演 绎 推 理 的 含 义
1、含义:从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理
演绎推理的一般模式:三段论
大前提-----
小前提-----
结论-----
2、三段论
已知的一般原理原理
所研究的特殊情况
根据一般原理,对特殊情况作出判断
概念归纳
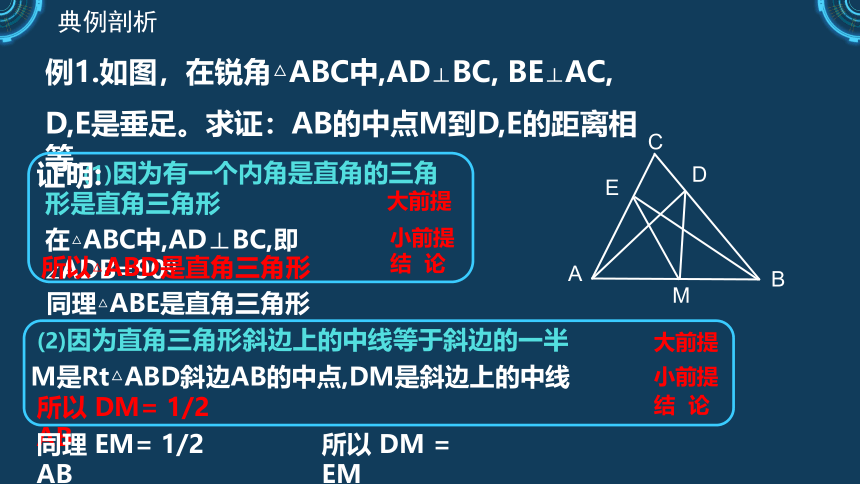
例1.如图,在锐角△ABC中,AD⊥BC, BE⊥AC,
D,E是垂足。求证:AB的中点M到D,E的距离相等.
(1)因为有一个内角是直角的三角形是直角三角形
证明:
大前提
在△ABC中,AD⊥BC,即∠ADB=900
小前提
所以△ABD是直角三角形
同理△ABE是直角三角形
(2)因为直角三角形斜边上的中线等于斜边的一半
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以 DM= 1/2 AB
同理 EM= 1/2 AB
大前提
小前提
结 论
结 论
所以 DM = EM
A
B
M
D
C
E
典例剖析
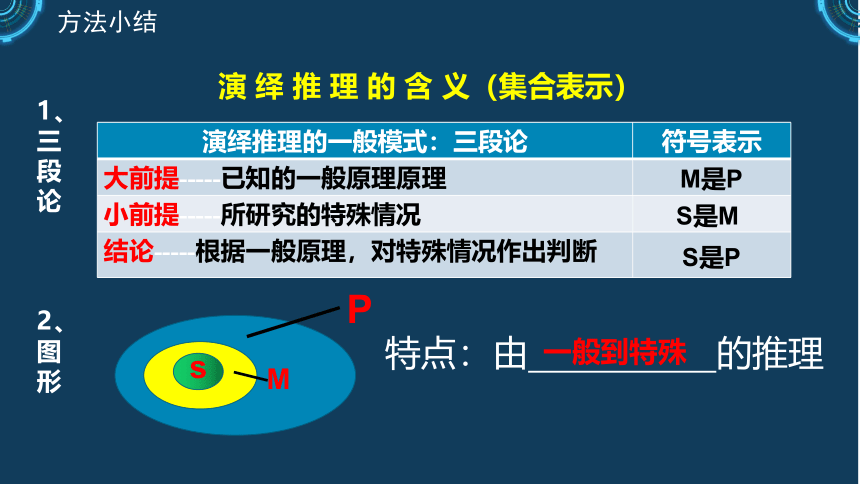
演 绎 推 理 的 含 义(集合表示)
演绎推理的一般模式:三段论 符号表示
大前提-----已知的一般原理原理
小前提-----所研究的特殊情况
结论-----根据一般原理,对特殊情况作出判断
MMM M
P
1、三段论
2、图形
特点:由 的推理
一般到特殊
M是P
S是M
S是P
方法小结
s
证明:
(方法1)
大前提
(可以省略)
小前提
结 论
在区间(a,b)内,若f′(x)>0,那么函数f(x)在区间(a,b)内单调递增.
所以函数f(x)=-x2+2x在(-∞,1]上是增函数
典例剖析
证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
证明:(方法2)
大前提
(可以省略)
小前提
结 论
满足对于任意x1,x2∈D,若x1任取x1,x2 ∈(-∞,1] 且x1f(x1)-f(x2)=(-x12+2x1)-(x22+2x2)
=(x2-x1)(x1+x2-2) 因为x10
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)所以函数f(x)=-x2+2x在(-∞,1]上是增函数.
典例剖析
证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
思考
在演绎推理中,只要前提和推理形式是正确的,结论必定正确。
演绎推理的结论一定正确吗?
因为指数函数 y=ax 是减函数,
而 y=2x 是指数函数,
所以 y=2x 是减函数。
错因:大前提是错误的,所以结论是错误的。
辨析知真
合情推理
归纳推理 类比推理 区别 推理形式
推理结论
联系 合情推理与演绎推理的区别与联系
演绎推理
由一般到特殊的推理
在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确
合情推理的结论需要演绎推理的验证,而演绎推理的方向和思路一般是通过合情推理获得的
课堂总结
由部分到整体、由个别到一般的推理
由特殊到特殊
的推理
结论不一定正确,有待进一步证明
高考链接
A
课堂检测
A
1、(提升题)如图:在△ABC中,AC>BC,CD是AB边上的高, 求证∠ACD>∠BCD。
错因:偷换概念。
证明:
在△ABC中,
因为CD⊥AB,AC>BC
所以AD>BD,
于是∠ACD>∠ BCD。
A
C
B
D
A
C
B
D
A
C
D
课堂检测
课后作业
导学案课后练习
感谢聆听!
北京师范大学银川学校
2.1.2 演绎推理
北京师范大学银川学校
2.1.2 演绎推理
2、合情推理的思维过程
合情推理
归纳推理
类比推理
1、合情推理的分类
复习回顾
一般原理 特殊情况 结论
所有金属都能导电 铜是金属
太阳系大行星以椭圆轨道绕太阳运行 天王星是太阳系的大行星
奇数都不能被2整除 2017是奇数
三角函数都是周期函数 因为三角函数
铜能导电
天王星以椭圆形轨道绕太阳运行
2017不能被2整除
所以是周期函数
观察发现
思考1:观察上述推理具有怎样的特征?
思考2:每一个例子由几部分组成?
演 绎 推 理 的 含 义
1、含义:从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理
演绎推理的一般模式:三段论
大前提-----
小前提-----
结论-----
2、三段论
已知的一般原理原理
所研究的特殊情况
根据一般原理,对特殊情况作出判断
概念归纳
例1.如图,在锐角△ABC中,AD⊥BC, BE⊥AC,
D,E是垂足。求证:AB的中点M到D,E的距离相等.
(1)因为有一个内角是直角的三角形是直角三角形
证明:
大前提
在△ABC中,AD⊥BC,即∠ADB=900
小前提
所以△ABD是直角三角形
同理△ABE是直角三角形
(2)因为直角三角形斜边上的中线等于斜边的一半
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以 DM= 1/2 AB
同理 EM= 1/2 AB
大前提
小前提
结 论
结 论
所以 DM = EM
A
B
M
D
C
E
典例剖析
演 绎 推 理 的 含 义(集合表示)
演绎推理的一般模式:三段论 符号表示
大前提-----已知的一般原理原理
小前提-----所研究的特殊情况
结论-----根据一般原理,对特殊情况作出判断
MMM M
P
1、三段论
2、图形
特点:由 的推理
一般到特殊
M是P
S是M
S是P
方法小结
s
证明:
(方法1)
大前提
(可以省略)
小前提
结 论
在区间(a,b)内,若f′(x)>0,那么函数f(x)在区间(a,b)内单调递增.
所以函数f(x)=-x2+2x在(-∞,1]上是增函数
典例剖析
证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
证明:(方法2)
大前提
(可以省略)
小前提
结 论
满足对于任意x1,x2∈D,若x1
=(x2-x1)(x1+x2-2) 因为x1
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)
典例剖析
证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
思考
在演绎推理中,只要前提和推理形式是正确的,结论必定正确。
演绎推理的结论一定正确吗?
因为指数函数 y=ax 是减函数,
而 y=2x 是指数函数,
所以 y=2x 是减函数。
错因:大前提是错误的,所以结论是错误的。
辨析知真
合情推理
归纳推理 类比推理 区别 推理形式
推理结论
联系 合情推理与演绎推理的区别与联系
演绎推理
由一般到特殊的推理
在大前提、小前提和推理形式都正确的前提下,得到的结论一定正确
合情推理的结论需要演绎推理的验证,而演绎推理的方向和思路一般是通过合情推理获得的
课堂总结
由部分到整体、由个别到一般的推理
由特殊到特殊
的推理
结论不一定正确,有待进一步证明
高考链接
A
课堂检测
A
1、(提升题)如图:在△ABC中,AC>BC,CD是AB边上的高, 求证∠ACD>∠BCD。
错因:偷换概念。
证明:
在△ABC中,
因为CD⊥AB,AC>BC
所以AD>BD,
于是∠ACD>∠ BCD。
A
C
B
D
A
C
B
D
A
C
D
课堂检测
课后作业
导学案课后练习
感谢聆听!
北京师范大学银川学校
