1.3.2函数的极值与导数 说课课件(46张PPT)
文档属性
| 名称 | 1.3.2函数的极值与导数 说课课件(46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 13:14:45 | ||
图片预览










文档简介
(共46张PPT)
1.3.2函数的极值与导数
高中数学 人教A版 选修2-2
目录
Contents
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
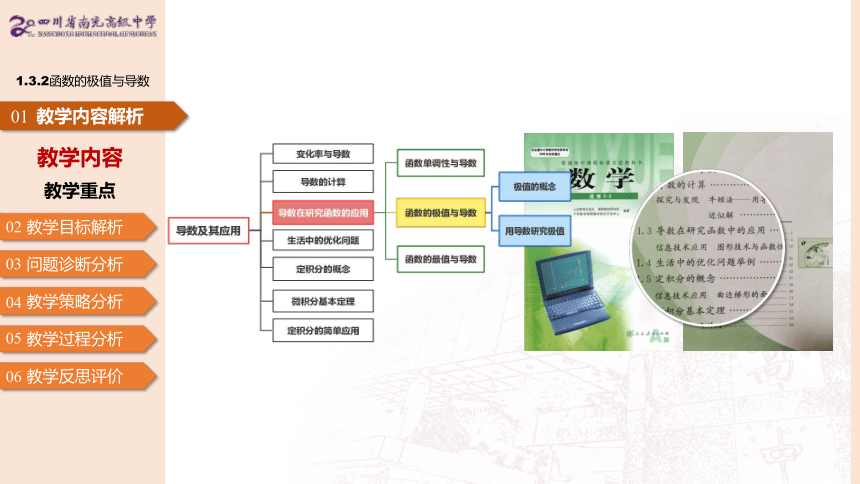
极值
局部范围内的最值——“单调性转折点”
单调性
基本初等函数——定义法;
复杂函数——
导数
定量刻画函数的局部变化规律,是基本工具.
导数
?
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
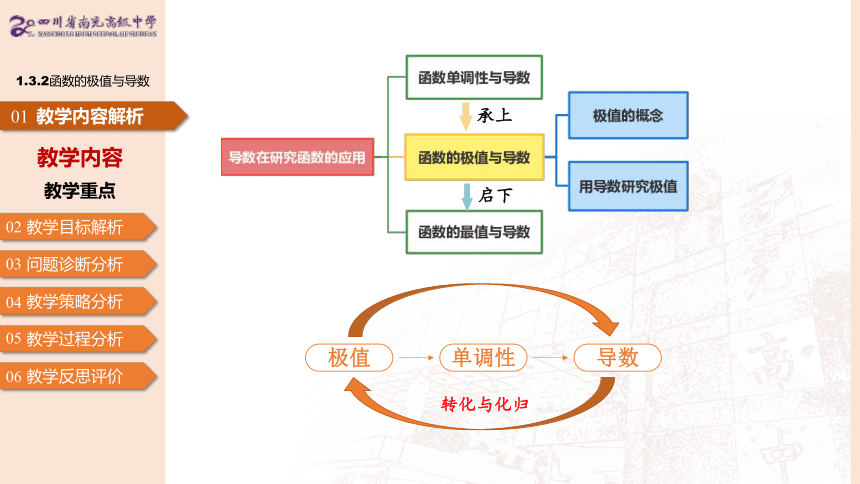
极值
单调性
导数
转化与化归
承上
启下
教学内容
教学重点
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
函数极值的概念
教学重点
利用导数求函数的极值
1.3.2函数的极值与导数
教学内容解析
01
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
教学目标解析
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
②借助函数的图象,了解函数在某点取得极值的必要条件和充分条件;能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值;体会导数与单调性、极值、最大 (小)值的关系.
①结合实例,借助几何直观了解函数的单调性与导数的关系;能利用导数研究函数的单调性;对于多项式函数,能求不超过三次的多项式函数的单调区间.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
学情分析
教学难点
授课对象是南充高中高二学生
较好的观察分析、抽象概括的能力.
已具备的认知基础:
学生具备知识基础、活动经验、运用意识.
可能出现的障碍:
极值概念理论性强,对学生思维要求高.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
学情分析
教学难点
极值的概念理解
函数的极值与导数的关系
教学难点
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
教学策略
问题引导 明确方向
自主探究 合作交流
转化与化归
极值是什么 怎么求
理解概念
掌握方法
教师为主导
学生为主体
知识为主线
思维为主旨
问题探究式教学法
——
试错
转化
验证
结论
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
通过滑雪大跳台等实例,引导学生借助几何直观,经历“极值”概念的生成过程,尊重学生认知规律,通过师生共同设疑探讨,将高等数学中的“邻域”通过“画圈”形象地刻画.
以徐利治RMI原理为指导,以三次多项式函数为载体,通过自主探究、合作交流,将求函数的极值点问题映射到求导函数的变号零点问题,问题转化,以退为进,规范板书,步骤程序化.
教学难点
难点突破
问题探究式教学法
教学策略
理解函数的极值
与导数的关系
理解极值的概念
教师为主导
学生为主体
知识为主线
思维为主旨
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
巩固拓展
概念应用
循序渐进 发展素养
目标检测检验效果
课堂小结
形成系统
生成概念
内涵辨析
创设情境提出问题
作业布置
分层提升
函数的单调性与导数——实践作业成果展示
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
创设情境 提出问题
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
滑雪大跳台
紧跟时代热点,
创造适合情境,
调动学习兴趣,
激发爱国情怀.
高台跳水
群山风景
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
创设情境 提出问题
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
高台跳水
滑雪大跳台
群山风景
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
单调性变化的转折点
波峰波谷
教学反思评价
06
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
局部最值
创设情境 提出问题
生成概念 内涵辨析
环节一:生成极值概念
积累数学活动经验,
发展数学抽象核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
y = f (x)
极小值点
极大值点
函数 在点 的函数值 比它在点 附近其他点的函数值都小,我们把点 叫做函数 极小值点,叫做函数 的极小值.
【图象角度】
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
函数 在点 b 的函数值 比它在点 附近其他点的函数值都大,我们把点 叫做函数 极大值点,叫做函数 的极大值.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
以“群山曲线”为载体,讨论交流,理解概念.
设计
意图
生成概念 内涵辨析
巩固拓展 概念应用
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
第一组分享
”—左右邻居
疑惑:是极大值点吗?
结论:端点不是极值点
追问:
教师追问
方法:“”
第六组分享
教师确认
“”—不是任意,而是存在
理解概念 达成目标
生成概念 内涵辨析
巩固拓展 概念应用
第八组分享
同意第六组
立德树人
不惧低谷 勇攀顶峰
环节二:极值内涵辨析
登峰造极
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
登峰造极
不惧低谷 勇攀顶峰
设计意图
挖掘内涵,深度辨析,考虑问题严谨的同时,也尊重学生认知规律. 发展学生直观想象核心素养. 落实“立德树人”育人目标.
生成概念 内涵辨析
巩固拓展 概念应用
第一组分享
”—左右邻居
结论:端点不是极值点
追问:
教师追问
方法:“”
第六组分享
教师确认
“”—不是任意,而是存在
理解概念 达成目标
第八组分享
同意第六组
疑惑:是极大值点吗?
立德树人
不惧低谷 勇攀顶峰
登峰造极
1.3.2函数的极值与导数
理解概念 达成目标
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
创设情境 提出问题
教学反思评价
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
01
02
03
04
05
06
生成概念 内涵辨析
巩固拓展 概念应用
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
设置基本初等函数,通过图象快速判断,巩固极值概念,获得发展所必需的数学基础知识和基本技能,体现数形结合思想,培养学生直观想象的数学核心素养.
设计
意图
例1 判断下列函数是否有极值,如果有,是极小值还是极大值.
环节三:利用导数求函数极值
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
例2 判断函数是否有极值?如果有,求出极值.
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
方法:定义
第四组分享
第二组帮助
“”—— 存在
师生共同操作确认
质疑:万一先减后增再减呢?
结论:先增后减
困难:先增后减?
回归定义
以三次函数“逼迫”学生另寻他法,层层展开的探讨,激活学生“最近发展区”,自然合理引出导数,发展直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
试错
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
方法:定义
第四组分享
第二组帮助
“”—— 存在
师生共同操作确认
质疑:万一先减后增再减呢?
结论:先增后减
困难:先增后减?
回归定义
转化
验证
结论
用导数研究函数
例2 判断函数是否有极值?如果有,求出极值.
以三次函数“逼迫”学生另寻他法,层层展开的探讨,激活学生“最近发展区”,自然合理引出导数,发展直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
导数几何意义
左负右正中间值为0
极小值——左负右正
极大值——左正右负
第3组成果
第6组成果
环节四:
函数的极值与导数关系
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
原函数的极值点——导函数的变号零点
借助几何直观,让学生“看得见”、“说得出”,对于直观结果,可以深刻到符号化水平去刻画,发展学生直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
定义域优先
1.函数求导
2.方程求根
3.列表判号
4.求出极值
基础知识
巩固拓展 概念应用
目标检测 检验效果
可导函数的极值点
导函数的变号零点
对应
方程的根
化归
基本技能
活动经验
基本思想
教师示范 学生总结
师生合作 点明核心
数学运算
逻辑推理
解题步骤:
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
体会导数的工具性、优越性
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
意外之喜
作出图象
1.3.2函数的极值与导数
掌握方法 达成目标
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
导数值为 0 是函数在该点取极值的必要不充分条件
设计意图
主要检测学生利用导数研究函数极值的方法和步骤,学生充分展现自我,获得不同的数学体验.
目标检测
目标检测 检验效果
1.3.2函数的极值与导数
完成检测 达成目标
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
课堂小结 形成系统
“我学会了极值的概念”
“我体会到了导数在解决函数问题的重要性”
数形结合
“数学与生活息息相关,要用数学的眼光看世界”
“极值不一定是最值,
我们要不同角度看待问题”
……
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
课堂教学思维导图
理清知识结构,提炼数学方法,感悟数学思想,发生数学素养.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
教材课后练习题,巩固极值概念重视基础知识和基本技能.
用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界.
极值定义拓展阅读,既不影响主体知识建构,又能使学有余力的学生得到进一步发展.
“不同的人在数学上得到不同的发展.”
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
数学知识的“学术形态”转化为数学课堂的“教学形态”
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
原函数的极值问题
导函数变号零点问题
映射
导函数有变号零点
代数运算
原函数有极值
反演
徐利治先生关系—映射—反演(RMI)原理
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
“研究对象在变,思想方法不变,研究套路不变”
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
实现教学目标,
提升核心素养!发现问题、提出问题、
分析问题、解决问题.
敬请批评指正!
高中数学 人教A版 选修2-2
1.3.2函数的极值与导数
高中数学 人教A版 选修2-2
目录
Contents
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
极值
局部范围内的最值——“单调性转折点”
单调性
基本初等函数——定义法;
复杂函数——
导数
定量刻画函数的局部变化规律,是基本工具.
导数
?
教学内容
教学重点
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
教学反思评价
1.3.2函数的极值与导数
01
02
03
04
05
06
极值
单调性
导数
转化与化归
承上
启下
教学内容
教学重点
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
函数极值的概念
教学重点
利用导数求函数的极值
1.3.2函数的极值与导数
教学内容解析
01
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
教学目标解析
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
②借助函数的图象,了解函数在某点取得极值的必要条件和充分条件;能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值;体会导数与单调性、极值、最大 (小)值的关系.
①结合实例,借助几何直观了解函数的单调性与导数的关系;能利用导数研究函数的单调性;对于多项式函数,能求不超过三次的多项式函数的单调区间.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
学情分析
教学难点
授课对象是南充高中高二学生
较好的观察分析、抽象概括的能力.
已具备的认知基础:
学生具备知识基础、活动经验、运用意识.
可能出现的障碍:
极值概念理论性强,对学生思维要求高.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
学情分析
教学难点
极值的概念理解
函数的极值与导数的关系
教学难点
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
教学策略
问题引导 明确方向
自主探究 合作交流
转化与化归
极值是什么 怎么求
理解概念
掌握方法
教师为主导
学生为主体
知识为主线
思维为主旨
问题探究式教学法
——
试错
转化
验证
结论
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
通过滑雪大跳台等实例,引导学生借助几何直观,经历“极值”概念的生成过程,尊重学生认知规律,通过师生共同设疑探讨,将高等数学中的“邻域”通过“画圈”形象地刻画.
以徐利治RMI原理为指导,以三次多项式函数为载体,通过自主探究、合作交流,将求函数的极值点问题映射到求导函数的变号零点问题,问题转化,以退为进,规范板书,步骤程序化.
教学难点
难点突破
问题探究式教学法
教学策略
理解函数的极值
与导数的关系
理解极值的概念
教师为主导
学生为主体
知识为主线
思维为主旨
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
巩固拓展
概念应用
循序渐进 发展素养
目标检测检验效果
课堂小结
形成系统
生成概念
内涵辨析
创设情境提出问题
作业布置
分层提升
函数的单调性与导数——实践作业成果展示
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
创设情境 提出问题
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
滑雪大跳台
紧跟时代热点,
创造适合情境,
调动学习兴趣,
激发爱国情怀.
高台跳水
群山风景
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
创设情境 提出问题
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
高台跳水
滑雪大跳台
群山风景
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
单调性变化的转折点
波峰波谷
教学反思评价
06
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
局部最值
创设情境 提出问题
生成概念 内涵辨析
环节一:生成极值概念
积累数学活动经验,
发展数学抽象核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
y = f (x)
极小值点
极大值点
函数 在点 的函数值 比它在点 附近其他点的函数值都小,我们把点 叫做函数 极小值点,叫做函数 的极小值.
【图象角度】
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
函数 在点 b 的函数值 比它在点 附近其他点的函数值都大,我们把点 叫做函数 极大值点,叫做函数 的极大值.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
以“群山曲线”为载体,讨论交流,理解概念.
设计
意图
生成概念 内涵辨析
巩固拓展 概念应用
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
第一组分享
”—左右邻居
疑惑:是极大值点吗?
结论:端点不是极值点
追问:
教师追问
方法:“”
第六组分享
教师确认
“”—不是任意,而是存在
理解概念 达成目标
生成概念 内涵辨析
巩固拓展 概念应用
第八组分享
同意第六组
立德树人
不惧低谷 勇攀顶峰
环节二:极值内涵辨析
登峰造极
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
登峰造极
不惧低谷 勇攀顶峰
设计意图
挖掘内涵,深度辨析,考虑问题严谨的同时,也尊重学生认知规律. 发展学生直观想象核心素养. 落实“立德树人”育人目标.
生成概念 内涵辨析
巩固拓展 概念应用
第一组分享
”—左右邻居
结论:端点不是极值点
追问:
教师追问
方法:“”
第六组分享
教师确认
“”—不是任意,而是存在
理解概念 达成目标
第八组分享
同意第六组
疑惑:是极大值点吗?
立德树人
不惧低谷 勇攀顶峰
登峰造极
1.3.2函数的极值与导数
理解概念 达成目标
教学内容解析
教学目标解析
问题诊断分析
教学策略分析
教学过程分析
创设情境 提出问题
教学反思评价
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
01
02
03
04
05
06
生成概念 内涵辨析
巩固拓展 概念应用
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
设置基本初等函数,通过图象快速判断,巩固极值概念,获得发展所必需的数学基础知识和基本技能,体现数形结合思想,培养学生直观想象的数学核心素养.
设计
意图
例1 判断下列函数是否有极值,如果有,是极小值还是极大值.
环节三:利用导数求函数极值
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
例2 判断函数是否有极值?如果有,求出极值.
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
方法:定义
第四组分享
第二组帮助
“”—— 存在
师生共同操作确认
质疑:万一先减后增再减呢?
结论:先增后减
困难:先增后减?
回归定义
以三次函数“逼迫”学生另寻他法,层层展开的探讨,激活学生“最近发展区”,自然合理引出导数,发展直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
试错
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
方法:定义
第四组分享
第二组帮助
“”—— 存在
师生共同操作确认
质疑:万一先减后增再减呢?
结论:先增后减
困难:先增后减?
回归定义
转化
验证
结论
用导数研究函数
例2 判断函数是否有极值?如果有,求出极值.
以三次函数“逼迫”学生另寻他法,层层展开的探讨,激活学生“最近发展区”,自然合理引出导数,发展直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
导数几何意义
左负右正中间值为0
极小值——左负右正
极大值——左正右负
第3组成果
第6组成果
环节四:
函数的极值与导数关系
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
原函数的极值点——导函数的变号零点
借助几何直观,让学生“看得见”、“说得出”,对于直观结果,可以深刻到符号化水平去刻画,发展学生直观想象、逻辑推理核心素养.
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
定义域优先
1.函数求导
2.方程求根
3.列表判号
4.求出极值
基础知识
巩固拓展 概念应用
目标检测 检验效果
可导函数的极值点
导函数的变号零点
对应
方程的根
化归
基本技能
活动经验
基本思想
教师示范 学生总结
师生合作 点明核心
数学运算
逻辑推理
解题步骤:
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
体会导数的工具性、优越性
无法判断是否有极值
困难:快速获取图象
方法:描点法
困难:不同图不一致
第五组分享
意外之喜
作出图象
1.3.2函数的极值与导数
掌握方法 达成目标
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
导数值为 0 是函数在该点取极值的必要不充分条件
设计意图
主要检测学生利用导数研究函数极值的方法和步骤,学生充分展现自我,获得不同的数学体验.
目标检测
目标检测 检验效果
1.3.2函数的极值与导数
完成检测 达成目标
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
课堂小结 形成系统
作业布置 分层提升
巩固拓展 概念应用
目标检测 检验效果
例题练习 掌握方法
抽象实例 生成概念
目标检测 深化概念
贴近生活 立德树人
通过具体实例抽象出函数图象,借助函数图象感知“波峰波谷” “单调性转折点”,生成极值概念,体会类比、数形结合思想,发展数学抽象、数学建模核心素养.
通过三次多项式函数的极值判断,将可导函数的极值点对应到求导函数的变号零点,掌握用导数求函数极值的方法和步骤,领悟函数与方程、转化与化归思想,发展学生数学运算、逻辑推理核心素养.
通过判断函数是否有极值,理解函数在某点取得极值的必要条件和充分条件,发展学生逻辑推理、直观想象核心素养.
通过群山起伏建立“不惧低谷”信心,树立全面看待事物的世界观, 体会极值与最值、局部与整体的关系,培养 “全局观”,落实“立德树人”育人目标.
1
2
3
4
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
课堂小结 形成系统
“我学会了极值的概念”
“我体会到了导数在解决函数问题的重要性”
数形结合
“数学与生活息息相关,要用数学的眼光看世界”
“极值不一定是最值,
我们要不同角度看待问题”
……
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
课堂教学思维导图
理清知识结构,提炼数学方法,感悟数学思想,发生数学素养.
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
创设情境 提出问题
教学反思评价
06
生成概念 内涵辨析
巩固拓展 概念应用
目标检测 检验效果
课堂小结 形成系统
作业布置 分层提升
教材课后练习题,巩固极值概念重视基础知识和基本技能.
用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界.
极值定义拓展阅读,既不影响主体知识建构,又能使学有余力的学生得到进一步发展.
“不同的人在数学上得到不同的发展.”
设计
意图
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
数学知识的“学术形态”转化为数学课堂的“教学形态”
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
原函数的极值问题
导函数变号零点问题
映射
导函数有变号零点
代数运算
原函数有极值
反演
徐利治先生关系—映射—反演(RMI)原理
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
“研究对象在变,思想方法不变,研究套路不变”
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
1.3.2函数的极值与导数
教学内容解析
01
教学目标解析
02
问题诊断分析
03
教学策略分析
04
教学过程分析
05
教学反思评价
06
为什么?
函数的极值与导数的关系(难点)
(基本思想、基本活动经验)
会用数学的思维思考世界
怎么求?
利用导数求三次函数的极值的方法和步骤(重点)(基本技能)
会用数学的语言表达世界
是什么?
极值的概念
(重点、难点)(基础知识)
会用数学的眼光观察世界
实现教学目标,
提升核心素养!发现问题、提出问题、
分析问题、解决问题.
敬请批评指正!
高中数学 人教A版 选修2-2
