2022—2023学年人教版数学七年级下册 6.2立方根 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级下册 6.2立方根 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 15:02:47 | ||
图片预览






文档简介
(共17张PPT)
6.2
立方根
第六章 实数
学习目标
1. 了解立方根的概念,掌握立方根的性质特征和一些重要结论.
2. 探究立方根的移位规律,并根据规律求一个数的立方根.
3. 会进行带立方根的两个数的大小比较.
引入
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多少?
:设这种包装箱的棱长为
∵
∴
∴这种包装箱的棱长应该为3m.
立方根概念
(1)平方根的概念: 如果一个数的平方等于 a ,
(1)平方根的概念: 那么这个数叫做 a 的平方根或二次方根.
(2)立方根的概念: 如果一个数的立方等于 a ,
(2)立方根的概念: 那么这个数叫做 a 的立方根或三次方根.
符号表示:
读作:“三次根号a”,其中a是被开方数,3是根指数.
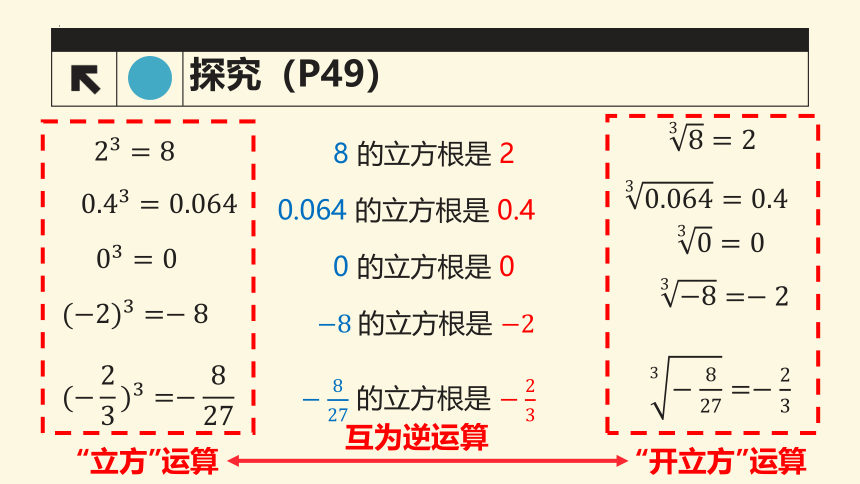
探究(P49)
8 的立方根是 2
0.064 的立方根是 0.4
0 的立方根是 0
的立方根是
的立方根是
“立方”运算
“开立方”运算
互为逆运算
探究
正数、负数和0的立方根各有什么特点?
归纳:
正数的立方根是正数,
负数的立方根是负数,
0的立方根是0.
探究:平方根与立方根性质特征的异同
平方根 立方根
正数 有两个平方根,它们互为相反数 有一个正的立方根
0 0 0
负数 没有平方根 有一个负的立方根
小结 常用的立方数表
跟踪训练1
(1)算数平方根等于它本身的数是______.
(2)平方根等于它本身的数是______.
(3)立方根等于它本身的数是______.
跟踪训练2:求下列各式的值
(1);(2);(3).
探究1:求下列各式的值,你能发现什么?
(1) (2) (3)
(4) (5) (6)
结论:
探究2:求下列各式的值,你能发现什么?
(1) (2)
(3) (4)
结论2:
探究3:找规律
……
规律:
被开方数的小数点向右或向左每移动 3 位,
它的立方根的小数点就相应的向右或向左移动 1 位;
跟踪训练3:求下列各式的值
(1)已知 ,
(1)则_____, _____,_____.
(2)已知 ,
(1)则______, ______,______.
(3)若n < < n+1(其中n为正整数),则n= .
跟踪训练4
P51 练习3.
小结
作业
3
6.2
立方根
第六章 实数
学习目标
1. 了解立方根的概念,掌握立方根的性质特征和一些重要结论.
2. 探究立方根的移位规律,并根据规律求一个数的立方根.
3. 会进行带立方根的两个数的大小比较.
引入
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多少?
:设这种包装箱的棱长为
∵
∴
∴这种包装箱的棱长应该为3m.
立方根概念
(1)平方根的概念: 如果一个数的平方等于 a ,
(1)平方根的概念: 那么这个数叫做 a 的平方根或二次方根.
(2)立方根的概念: 如果一个数的立方等于 a ,
(2)立方根的概念: 那么这个数叫做 a 的立方根或三次方根.
符号表示:
读作:“三次根号a”,其中a是被开方数,3是根指数.
探究(P49)
8 的立方根是 2
0.064 的立方根是 0.4
0 的立方根是 0
的立方根是
的立方根是
“立方”运算
“开立方”运算
互为逆运算
探究
正数、负数和0的立方根各有什么特点?
归纳:
正数的立方根是正数,
负数的立方根是负数,
0的立方根是0.
探究:平方根与立方根性质特征的异同
平方根 立方根
正数 有两个平方根,它们互为相反数 有一个正的立方根
0 0 0
负数 没有平方根 有一个负的立方根
小结 常用的立方数表
跟踪训练1
(1)算数平方根等于它本身的数是______.
(2)平方根等于它本身的数是______.
(3)立方根等于它本身的数是______.
跟踪训练2:求下列各式的值
(1);(2);(3).
探究1:求下列各式的值,你能发现什么?
(1) (2) (3)
(4) (5) (6)
结论:
探究2:求下列各式的值,你能发现什么?
(1) (2)
(3) (4)
结论2:
探究3:找规律
……
规律:
被开方数的小数点向右或向左每移动 3 位,
它的立方根的小数点就相应的向右或向左移动 1 位;
跟踪训练3:求下列各式的值
(1)已知 ,
(1)则_____, _____,_____.
(2)已知 ,
(1)则______, ______,______.
(3)若n < < n+1(其中n为正整数),则n= .
跟踪训练4
P51 练习3.
小结
作业
3
