2022-2023学年七年级下学期数学人教版8.3二元一次方程 课件(共17张ppt)
文档属性
| 名称 | 2022-2023学年七年级下学期数学人教版8.3二元一次方程 课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 67.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 15:04:47 | ||
图片预览





文档简介
(共17张PPT)
《九章算术》与二元一次方程方程
九章算术
一、历史追踪
数学起源于人类的生产生活
一、历史追踪
人类从远古时代就开始积累数学知识
一、历史追踪
《九章算术》是中国古代第一步完整的数学著作
二、温故知新
活动一
1、上述所描的点的坐标都是适合关系式y=5-x?
2、上述所描的点,是否都在一次函数y=5-x的图象上?
3、在一次函数y=5-x的图象上任取一个点,它的坐标满足方程x+y=5吗?
4、以方程x+y=5的解为坐标的所有的点所组成的图象,与一次函数y=5-x的图象相同吗?
1.方程x+y=5的解有多少个?请写出其中的几个(至少写出3个)
2.以上述解中x的值为横坐标,y的值为纵坐标,所得的点的坐标有哪些?
3.在平面直角坐标系中描出上述坐标所对应的点.
二、温故知新
活动二
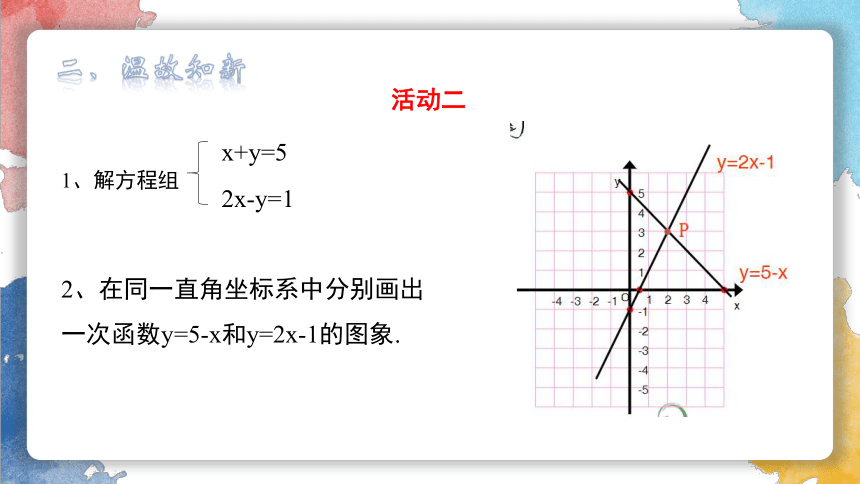
1、解方程组
x+y=5
2x-y=1
2、在同一直角坐标系中分别画出一次函数y=5-x和y=2x-1的图象.
二、温故知新
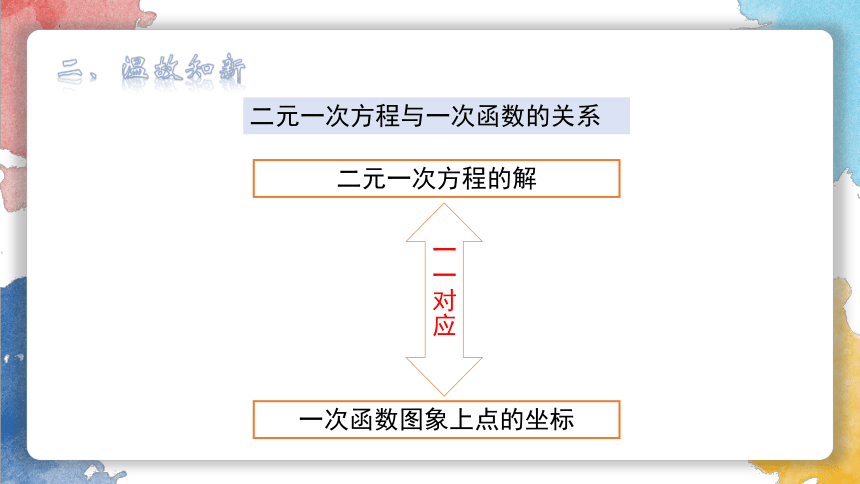
二元一次方程的解
一次函数图象上点的坐标
一一对应
二元一次方程与一次函数的关系
今有共买物,人出八,盈三;人出七,不足四。
二、自主探究
译:
有一些人共同买一个物品,每人出8元,还盈余3元,每人出7元,则还差4元。
盈不足
设人数为x,
则有:8x-3=7x+4
二元一次方程
一元一次方程
设人数为x,物价为y,则:
8x=y+3
7x=y-4
x=7
y=53
x=7
物价为:8×7-3=53
盈不足术
古今思异·一
置所出率,盈、不足各居其下。
令维乘所出率,并以为实。
并盈、不足为法。
盈不足相与同其买物者,置所出率,以少减多,余,以约法、实。
实为物价,法为人数。
今有共买物,人出八,盈三;人出七,不足四。
3
7 4
32+21=53 实
3+4=7 法
8-7=1 余
53 价
7 人
今有上禾三秉,中禾二秉,下禾一秉,共三十九斗;上禾二秉,中禾三秉,下禾一秉,共三十四斗;上禾一秉,中禾二,下禾三秉,共二十六斗。问上、中、下禾共一秉各几何?
二、自主探究
3束上等的稻,2束中等的稻,1束下等的稻,共出谷39斗;
2束上等的稻,3束中等的稻,1束下等的稻,共出谷34斗;
1束上等的稻,2束中等的稻,3束下等的稻,共出谷26斗.
问:上、中、下三种稻,每束的出谷量各是多少斗
3x+2y+z=39
2x+3y+z=34
x+2y+3z=26
设上等稻出谷量为x斗,中等稻出谷量为y斗,下等稻出谷量为z斗
古今思异·二
古今思异·二
方程術曰,置上禾三秉,中禾二秉,下禾一秉,實三十九斗,於右方。
中、左禾列如右方。以右行上禾遍乘中行而以直除。又乘其次,亦以直除。
然以中行中禾不盡者遍乘左行而以直除。
左方下禾不盡者,上為法,下為實。
實即下禾之實。
求中禾,以法乘中行下實,而除下禾之實。餘如中禾秉數而一,即中禾之實。
求上禾亦以法乘右行下實,而除下禾、中禾之實。餘如上禾秉數而一,即上禾之實。實皆如法,各得一斗。
方程术——直除法
古今思异·二
方程术——直除法
用算筹摆成“方阵”
遍乘直除(减)法
《九章算术》是世界上最早系统叙述了分数运算的著作,其中盈不足的算法更是一项令人惊奇的创造。
“方程”章还在世界数学史上最早提出负数概念及正负数加减法法则。
该书的一些知识还传播至印度和阿拉伯,甚至经过这些地区远至欧洲《九章算术》是几代人共同劳动的结晶,它的出现标志着中国古代数学体系的形成。
《九章算术》的历史影响:
三、源远流长
四、总结归纳
提炼
代入
加减
《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50,问:甲、乙两人各带了多少钱?设甲、乙两人持钱的数量分别为x,y,则可列方程组为( )
五、趁热打铁
《九章算术》与二元一次方程方程
九章算术
一、历史追踪
数学起源于人类的生产生活
一、历史追踪
人类从远古时代就开始积累数学知识
一、历史追踪
《九章算术》是中国古代第一步完整的数学著作
二、温故知新
活动一
1、上述所描的点的坐标都是适合关系式y=5-x?
2、上述所描的点,是否都在一次函数y=5-x的图象上?
3、在一次函数y=5-x的图象上任取一个点,它的坐标满足方程x+y=5吗?
4、以方程x+y=5的解为坐标的所有的点所组成的图象,与一次函数y=5-x的图象相同吗?
1.方程x+y=5的解有多少个?请写出其中的几个(至少写出3个)
2.以上述解中x的值为横坐标,y的值为纵坐标,所得的点的坐标有哪些?
3.在平面直角坐标系中描出上述坐标所对应的点.
二、温故知新
活动二
1、解方程组
x+y=5
2x-y=1
2、在同一直角坐标系中分别画出一次函数y=5-x和y=2x-1的图象.
二、温故知新
二元一次方程的解
一次函数图象上点的坐标
一一对应
二元一次方程与一次函数的关系
今有共买物,人出八,盈三;人出七,不足四。
二、自主探究
译:
有一些人共同买一个物品,每人出8元,还盈余3元,每人出7元,则还差4元。
盈不足
设人数为x,
则有:8x-3=7x+4
二元一次方程
一元一次方程
设人数为x,物价为y,则:
8x=y+3
7x=y-4
x=7
y=53
x=7
物价为:8×7-3=53
盈不足术
古今思异·一
置所出率,盈、不足各居其下。
令维乘所出率,并以为实。
并盈、不足为法。
盈不足相与同其买物者,置所出率,以少减多,余,以约法、实。
实为物价,法为人数。
今有共买物,人出八,盈三;人出七,不足四。
3
7 4
32+21=53 实
3+4=7 法
8-7=1 余
53 价
7 人
今有上禾三秉,中禾二秉,下禾一秉,共三十九斗;上禾二秉,中禾三秉,下禾一秉,共三十四斗;上禾一秉,中禾二,下禾三秉,共二十六斗。问上、中、下禾共一秉各几何?
二、自主探究
3束上等的稻,2束中等的稻,1束下等的稻,共出谷39斗;
2束上等的稻,3束中等的稻,1束下等的稻,共出谷34斗;
1束上等的稻,2束中等的稻,3束下等的稻,共出谷26斗.
问:上、中、下三种稻,每束的出谷量各是多少斗
3x+2y+z=39
2x+3y+z=34
x+2y+3z=26
设上等稻出谷量为x斗,中等稻出谷量为y斗,下等稻出谷量为z斗
古今思异·二
古今思异·二
方程術曰,置上禾三秉,中禾二秉,下禾一秉,實三十九斗,於右方。
中、左禾列如右方。以右行上禾遍乘中行而以直除。又乘其次,亦以直除。
然以中行中禾不盡者遍乘左行而以直除。
左方下禾不盡者,上為法,下為實。
實即下禾之實。
求中禾,以法乘中行下實,而除下禾之實。餘如中禾秉數而一,即中禾之實。
求上禾亦以法乘右行下實,而除下禾、中禾之實。餘如上禾秉數而一,即上禾之實。實皆如法,各得一斗。
方程术——直除法
古今思异·二
方程术——直除法
用算筹摆成“方阵”
遍乘直除(减)法
《九章算术》是世界上最早系统叙述了分数运算的著作,其中盈不足的算法更是一项令人惊奇的创造。
“方程”章还在世界数学史上最早提出负数概念及正负数加减法法则。
该书的一些知识还传播至印度和阿拉伯,甚至经过这些地区远至欧洲《九章算术》是几代人共同劳动的结晶,它的出现标志着中国古代数学体系的形成。
《九章算术》的历史影响:
三、源远流长
四、总结归纳
提炼
代入
加减
《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数甲得乙半而钱五十,乙得甲太半而亦钱五十.问:甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半,那么甲共有钱50;如果乙得到甲所有钱的,那么乙也共有钱50,问:甲、乙两人各带了多少钱?设甲、乙两人持钱的数量分别为x,y,则可列方程组为( )
五、趁热打铁
