2023年中考数学二轮复习:最值性问题(无答案)
文档属性
| 名称 | 2023年中考数学二轮复习:最值性问题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 18:18:48 | ||
图片预览

文档简介
中考数学二轮专题复习 最值问题
班级 姓名
最值性问题就是在已知条件下,探索目标的最大值或最小值,从而做出最优化的方案设计。其主要类型有:代数性最值、几何性最值两大类,在初中数学中代数性最值主要是通过建立对应的函数模型,利用函数图象与性质确定最值;几何性最值问题是指在一定条件下,求出平面几何图形中的某个确定的量(如线段的长度、角度的大小、图形的面积等)的最大值或最小值。常用方法有:(1)几何定理(公理)法构造图形:如两点之间线段最短,垂线段最短,平面内任意点到圆上的距离最长(最短)等,通过几何图形的模型构造法获得最佳方案。(2)数形结合法:揭示问题中变动的元素的代数关系,构造一元二次方程、二次函数 等求解。
两点之间线段最短
基本图形(和最小)
如图1,在直线上求作一点C使周长最短;
如图2,角内有一点A,请在角两边上求作点B,C使周长最短;
如图3,角内有两点D,E,请在角两边上求作点F,G使四边形DFEG周长最短。
如图4,A、B两村庄分别位于河两岸,现在需要建一座桥(河岸),使桥面与河岸保持垂直。求建一桥(作两点)使A、B之间的距离最短。
练习:
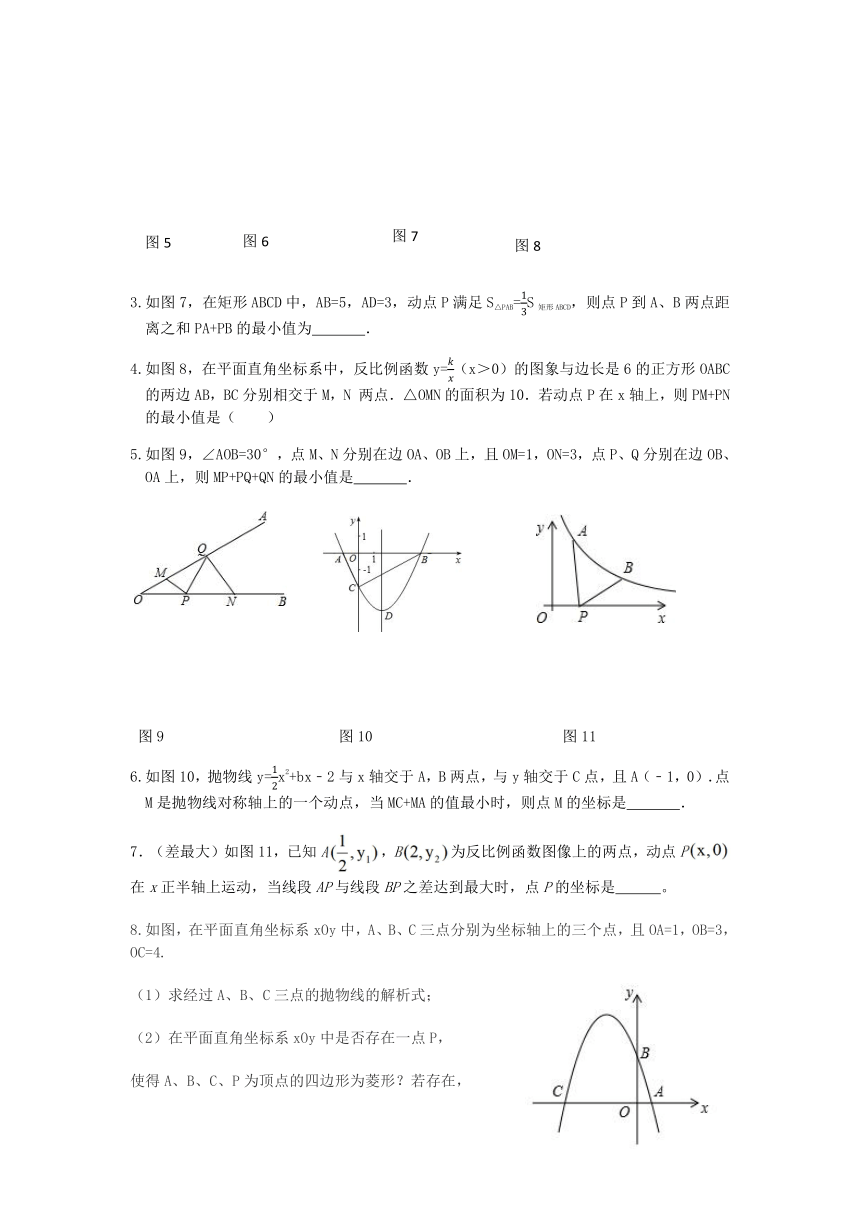
1.如图5,正方形ABCD的边长为2,E为BC的中点,P是BD上一动点.连接EP,CP,则EP+CP的最小值是 ;
2.如图6,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
3.如图7,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为 .
4.如图8,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
5.如图9,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是 .
图9 图10 图11
6.如图10,抛物线y=x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).点M是抛物线对称轴上的一个动点,当MC+MA的值最小时,则点M的坐标是 .
7.(差最大)如图11,已知A,B为反比例函数图像上的两点,动点P在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是 。
8.如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,
使得A、B、C、P为顶点的四边形为菱形?若存在,
请求出点P的坐标;若不存在,请说明理由。
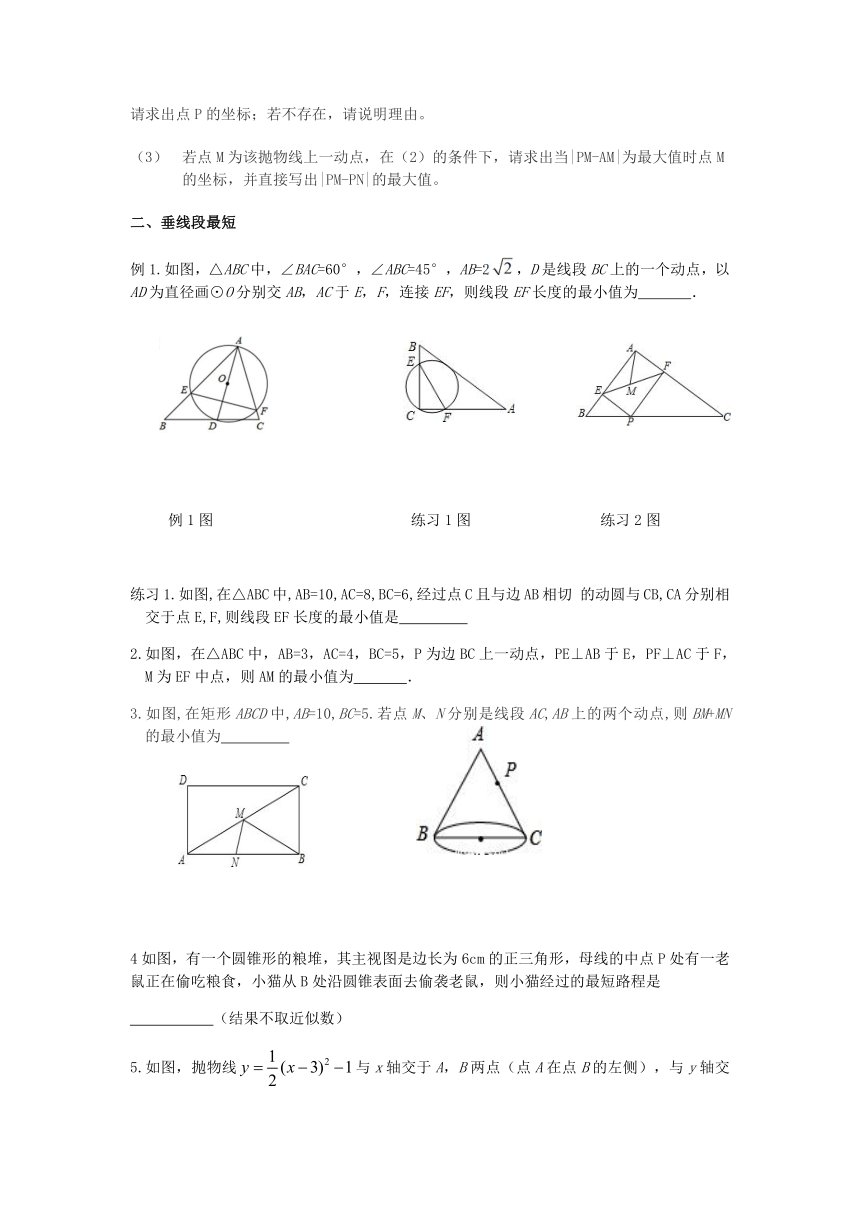
若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM-AM|为最大值时点M的坐标,并直接写出|PM-PN|的最大值。
二、垂线段最短
例1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
例1图 练习1图 练习2图
练习1.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切 的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是
2.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
3.如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为
4如图,有一个圆锥形的粮堆,其主视图是边长为6cm的正三角形,母线的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是
(结果不取近似数)
5.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D了.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD.求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
6.如图,抛物线y=ax2-5ax+c与坐标轴分别交于点A,C,E三点,其中A(-3,0),C(0,4),点B在轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.
三、圆中的最值问题
例2.平面内一点M,到圆上的最大距离为7cm,最小距离为3cm,则这个圆的半径为
例3.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
练习:
1.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为 .
2.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为,点D在第一象限,且,则线段CD的长的最小值为_________.
3.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为___.
4.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
5.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
A.2 B.1 C. D.
6、在中,若O为BC边的中点,则必有:成立。依据以上结论,解决如下问题.如图,在矩形DEFG中,已知DE=4,EF=3。点P在以DE为直径的半圆上运动,则的最小值为_____.
四.建立函数模型解决最值问题
例4. 如图对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式.
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
练习:
1.如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(﹣4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
2.如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
3.用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
4.在等腰△ABC中,AB=AC=5,BC=6,动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC,将△AMN沿MN所在的直线折叠,使点A的对应点为P。
(1)当MN为何值时,点P恰好落在BC上?
(2)当MN=x,△MNP与等腰△ABC重叠部分的
面积为y,试写出y与x的函数关系式,当x为
何值时,y的值最大,最大值是多少?
班级 姓名
最值性问题就是在已知条件下,探索目标的最大值或最小值,从而做出最优化的方案设计。其主要类型有:代数性最值、几何性最值两大类,在初中数学中代数性最值主要是通过建立对应的函数模型,利用函数图象与性质确定最值;几何性最值问题是指在一定条件下,求出平面几何图形中的某个确定的量(如线段的长度、角度的大小、图形的面积等)的最大值或最小值。常用方法有:(1)几何定理(公理)法构造图形:如两点之间线段最短,垂线段最短,平面内任意点到圆上的距离最长(最短)等,通过几何图形的模型构造法获得最佳方案。(2)数形结合法:揭示问题中变动的元素的代数关系,构造一元二次方程、二次函数 等求解。
两点之间线段最短
基本图形(和最小)
如图1,在直线上求作一点C使周长最短;
如图2,角内有一点A,请在角两边上求作点B,C使周长最短;
如图3,角内有两点D,E,请在角两边上求作点F,G使四边形DFEG周长最短。
如图4,A、B两村庄分别位于河两岸,现在需要建一座桥(河岸),使桥面与河岸保持垂直。求建一桥(作两点)使A、B之间的距离最短。
练习:
1.如图5,正方形ABCD的边长为2,E为BC的中点,P是BD上一动点.连接EP,CP,则EP+CP的最小值是 ;
2.如图6,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
3.如图7,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为 .
4.如图8,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
5.如图9,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是 .
图9 图10 图11
6.如图10,抛物线y=x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).点M是抛物线对称轴上的一个动点,当MC+MA的值最小时,则点M的坐标是 .
7.(差最大)如图11,已知A,B为反比例函数图像上的两点,动点P在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是 。
8.如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,
使得A、B、C、P为顶点的四边形为菱形?若存在,
请求出点P的坐标;若不存在,请说明理由。
若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM-AM|为最大值时点M的坐标,并直接写出|PM-PN|的最大值。
二、垂线段最短
例1.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
例1图 练习1图 练习2图
练习1.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切 的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是
2.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
3.如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为
4如图,有一个圆锥形的粮堆,其主视图是边长为6cm的正三角形,母线的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是
(结果不取近似数)
5.如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D了.
(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接AE,AD.求证:∠AEO=∠ADC;
(3)以(2)中的点E为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P作⊙E的切线,切点为Q,当PQ的长最小时,求点P的坐标,并直接写出点Q的坐标.
6.如图,抛物线y=ax2-5ax+c与坐标轴分别交于点A,C,E三点,其中A(-3,0),C(0,4),点B在轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.
三、圆中的最值问题
例2.平面内一点M,到圆上的最大距离为7cm,最小距离为3cm,则这个圆的半径为
例3.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
练习:
1.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为 .
2.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为,点D在第一象限,且,则线段CD的长的最小值为_________.
3.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为___.
4.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
5.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
A.2 B.1 C. D.
6、在中,若O为BC边的中点,则必有:成立。依据以上结论,解决如下问题.如图,在矩形DEFG中,已知DE=4,EF=3。点P在以DE为直径的半圆上运动,则的最小值为_____.
四.建立函数模型解决最值问题
例4. 如图对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式.
(2)当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
练习:
1.如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(﹣4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
2.如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
3.用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
4.在等腰△ABC中,AB=AC=5,BC=6,动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC,将△AMN沿MN所在的直线折叠,使点A的对应点为P。
(1)当MN为何值时,点P恰好落在BC上?
(2)当MN=x,△MNP与等腰△ABC重叠部分的
面积为y,试写出y与x的函数关系式,当x为
何值时,y的值最大,最大值是多少?
同课章节目录
