人教版2019选择性必修第一册 2.2简谐运动的描述(共26张PPT)
文档属性
| 名称 | 人教版2019选择性必修第一册 2.2简谐运动的描述(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 867.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-07 21:41:54 | ||
图片预览







文档简介
(共26张PPT)
§2.2 简谐运动的描述
弹簧振子的再研究
弹簧振子的运动特点:
1、围绕着“一个中心”位置
2、偏离“平衡位置”有最大位移
3、在两点间“往复”运动
对称性
往复性
复习回顾
我们学过的描述匀速圆周运动状态的物理量有哪些
速度
加速度
线速度
角速度
向心加速度
向心力
周期
频率
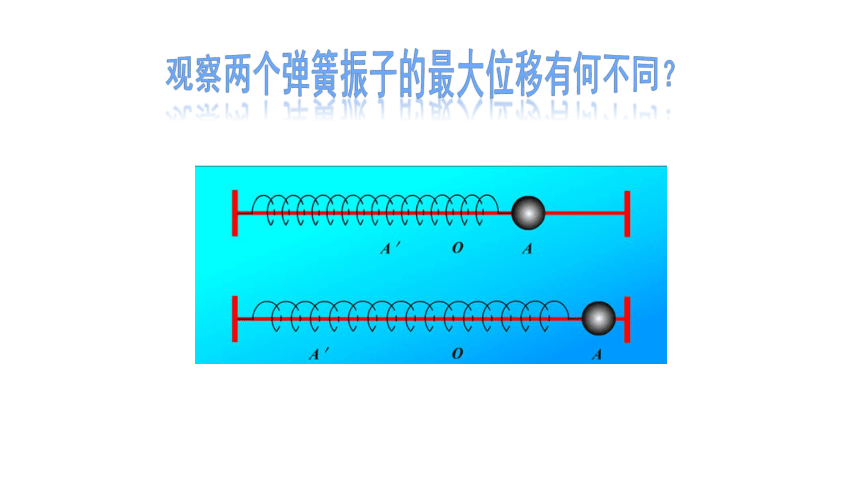
观察两个弹簧振子的最大位移有何不同?
描述简谐运动的物理量1:
振幅A:振动物体离开平衡位置的最大距离
①振幅的2倍表示振动物体运动范围的大小
②标量,反映振动的强弱.
O
x
振幅
振幅
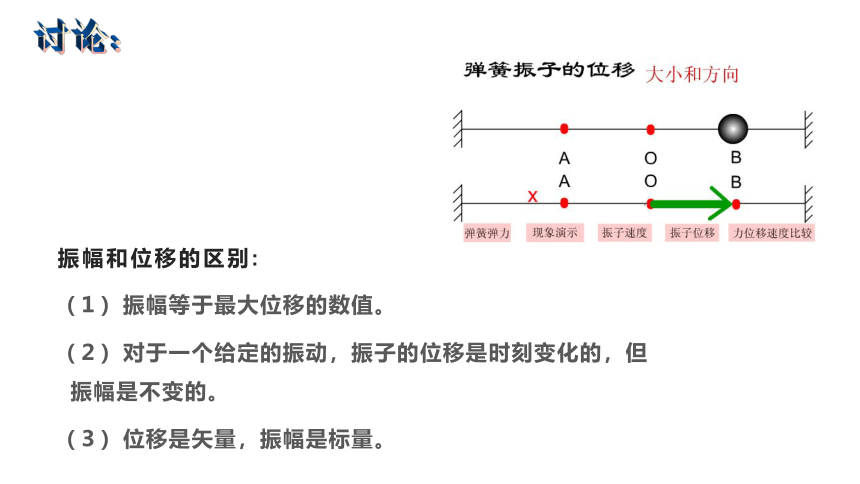
振幅和位移的区别:
(1)振幅等于最大位移的数值。
(2)对于一个给定的振动,振子的位移是时刻变化的,但振幅是不变的。
(3)位移是矢量,振幅是标量。
讨论:
观察三个振子的快慢有何不同?
描述简谐运动的物理量2:
全振动:一个完整的振动过程称为一次全振动.(振动质点连续两次以相同的速度通过同一点所经历的过程)
周期T:做简谐运动的物体完成一次全振动所需要的时间.
频率f:做简谐运动的物体单位时间内完成全振动的次数
f=1/T
弹簧振子的再研究
振子进行一次完整的振动(全振动)所经历的时间
问题1、O—D—B—D—O是一个周期吗?
问题2、若从振子经过C向右起,经过怎样的运动才叫完成一次全振动?
弹簧振子以O点为平衡位置在B、C两点间做简谐运动,BC相距20 cm,某时刻振子处于B点,经过0.5 s,振子首次到达C点。则振子的振幅A= cm;振子的周期T= s,频率f= Hz;振子在2 s内通过的路程大小s= cm;最大位移大小为x= cm。
解析 根据振幅的定义,有2A=BC=20 cm,所以A=10 cm。从B首次到C的时间为周期的一半,因此T=2t=1 s;再根据周期和频率的关系可得f= =1 Hz。振子一个周期通过的路程为4A=40 cm,则2 s内通过的路程为s= ·4A=2×40 cm=80 cm,最大位移大小等于振幅,x=10 cm。
答案 10 1 1 80 10
例1.
描述简谐运动的物理量3:
相位:
用来描述周期性运动在各个时刻所处的不同状态
x
t
描述简谐运动的物理量
相位
位置
简谐运动的表达式
振幅
圆频率
初相位
相位
简谐运动的表达式
振幅
周期
初相位
相位
简谐运动的表达式
简谐运动的位移和时间的关系可以用图象来表示为正弦或余弦曲线,如将这一关系表示为数学函数关系式应为:
振动方程中各变量的含义:
振动方程是位移x随时间t变化的函数关系式(位移方程).
1、 A 代表物体振动的振幅.
2、 叫做圆频率,表示简谐运动的快慢。
它与频率之间的关系为: =2 f
简谐运动的表达式
3、“ t+ ” 这个量就是简谐运动的相位,它是随时t不断变化的物理量,表示振动所处的状态.
4、相位差:常指两个具有相同频率的简谐运动的初相之差( 2- 1).对频率相同的两个简谐运动有确定的相位差.
叫初相位,简称初相,即t=0时的相位.
简谐运动的表达式
其它相关概念:
1、同相:
相位差为零,一般地为
=2n (n=0,1,2,……)
2、反相:
相位差为 ,一般地为
=(2n+1) (n=0,1,2,……)
例2.如图所示,一个弹簧振子沿x轴做简谐运动,其平衡位置在x轴坐标原点O处。从某时刻开始计时,经过四分之一的周期,振子具有沿x轴正方向的最大速度,图中能正确反映该弹簧振子的位移x与时间t关系的图像是( )
解析 振子具有沿x轴正方向的最大速度,一定运动到平衡位置,向x轴正方向运动,因此在0时刻,该振子一定位于负的最大位移处,故选B。
答案 B
一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时位移是4 cm,且向x轴负向运动,试写出用正弦函数表示的振动方程。
变式训练:
思维导图
对点训练
C
一弹簧振子做简谐运动,周期为T,则 ( )
A.若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相同,则Δt一定等于T的整数倍
B.若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等刻振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
对点训练
解析:弹簧振子做简谐运动的图像如图所示,图中A点与B、E、F、I等点的振动位移大小相等,方向相同。由图可知,A点与E、I等点对应的时间差为T或T的整数倍,A点与B、F等点对应的时间差不为T或T的整数倍,因此A选项不正确。
振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
§2.2 简谐运动的描述
弹簧振子的再研究
弹簧振子的运动特点:
1、围绕着“一个中心”位置
2、偏离“平衡位置”有最大位移
3、在两点间“往复”运动
对称性
往复性
复习回顾
我们学过的描述匀速圆周运动状态的物理量有哪些
速度
加速度
线速度
角速度
向心加速度
向心力
周期
频率
观察两个弹簧振子的最大位移有何不同?
描述简谐运动的物理量1:
振幅A:振动物体离开平衡位置的最大距离
①振幅的2倍表示振动物体运动范围的大小
②标量,反映振动的强弱.
O
x
振幅
振幅
振幅和位移的区别:
(1)振幅等于最大位移的数值。
(2)对于一个给定的振动,振子的位移是时刻变化的,但振幅是不变的。
(3)位移是矢量,振幅是标量。
讨论:
观察三个振子的快慢有何不同?
描述简谐运动的物理量2:
全振动:一个完整的振动过程称为一次全振动.(振动质点连续两次以相同的速度通过同一点所经历的过程)
周期T:做简谐运动的物体完成一次全振动所需要的时间.
频率f:做简谐运动的物体单位时间内完成全振动的次数
f=1/T
弹簧振子的再研究
振子进行一次完整的振动(全振动)所经历的时间
问题1、O—D—B—D—O是一个周期吗?
问题2、若从振子经过C向右起,经过怎样的运动才叫完成一次全振动?
弹簧振子以O点为平衡位置在B、C两点间做简谐运动,BC相距20 cm,某时刻振子处于B点,经过0.5 s,振子首次到达C点。则振子的振幅A= cm;振子的周期T= s,频率f= Hz;振子在2 s内通过的路程大小s= cm;最大位移大小为x= cm。
解析 根据振幅的定义,有2A=BC=20 cm,所以A=10 cm。从B首次到C的时间为周期的一半,因此T=2t=1 s;再根据周期和频率的关系可得f= =1 Hz。振子一个周期通过的路程为4A=40 cm,则2 s内通过的路程为s= ·4A=2×40 cm=80 cm,最大位移大小等于振幅,x=10 cm。
答案 10 1 1 80 10
例1.
描述简谐运动的物理量3:
相位:
用来描述周期性运动在各个时刻所处的不同状态
x
t
描述简谐运动的物理量
相位
位置
简谐运动的表达式
振幅
圆频率
初相位
相位
简谐运动的表达式
振幅
周期
初相位
相位
简谐运动的表达式
简谐运动的位移和时间的关系可以用图象来表示为正弦或余弦曲线,如将这一关系表示为数学函数关系式应为:
振动方程中各变量的含义:
振动方程是位移x随时间t变化的函数关系式(位移方程).
1、 A 代表物体振动的振幅.
2、 叫做圆频率,表示简谐运动的快慢。
它与频率之间的关系为: =2 f
简谐运动的表达式
3、“ t+ ” 这个量就是简谐运动的相位,它是随时t不断变化的物理量,表示振动所处的状态.
4、相位差:常指两个具有相同频率的简谐运动的初相之差( 2- 1).对频率相同的两个简谐运动有确定的相位差.
叫初相位,简称初相,即t=0时的相位.
简谐运动的表达式
其它相关概念:
1、同相:
相位差为零,一般地为
=2n (n=0,1,2,……)
2、反相:
相位差为 ,一般地为
=(2n+1) (n=0,1,2,……)
例2.如图所示,一个弹簧振子沿x轴做简谐运动,其平衡位置在x轴坐标原点O处。从某时刻开始计时,经过四分之一的周期,振子具有沿x轴正方向的最大速度,图中能正确反映该弹簧振子的位移x与时间t关系的图像是( )
解析 振子具有沿x轴正方向的最大速度,一定运动到平衡位置,向x轴正方向运动,因此在0时刻,该振子一定位于负的最大位移处,故选B。
答案 B
一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时位移是4 cm,且向x轴负向运动,试写出用正弦函数表示的振动方程。
变式训练:
思维导图
对点训练
C
一弹簧振子做简谐运动,周期为T,则 ( )
A.若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相同,则Δt一定等于T的整数倍
B.若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等刻振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
对点训练
解析:弹簧振子做简谐运动的图像如图所示,图中A点与B、E、F、I等点的振动位移大小相等,方向相同。由图可知,A点与E、I等点对应的时间差为T或T的整数倍,A点与B、F等点对应的时间差不为T或T的整数倍,因此A选项不正确。
振子运动速度的大小相等、方向相反,则Δt一定等于的整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
