【名校定制】(人教版)2014届八年级数学下册知识点汇聚测试卷:变量与函数(2014届中考冲刺复习通用,均含2013最新中考试题,含详解)
文档属性
| 名称 | 【名校定制】(人教版)2014届八年级数学下册知识点汇聚测试卷:变量与函数(2014届中考冲刺复习通用,均含2013最新中考试题,含详解) |
|
|
| 格式 | zip | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-20 00:00:00 | ||
图片预览


文档简介
变量与函数
一、选择题(每小题4分,共12分)
1.某型号的汽车在路面上的制动距离s=,其中变量是( )
A.s,v B.s,v2 C.s D.v
2.(2013·泸州中考)函数y=自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
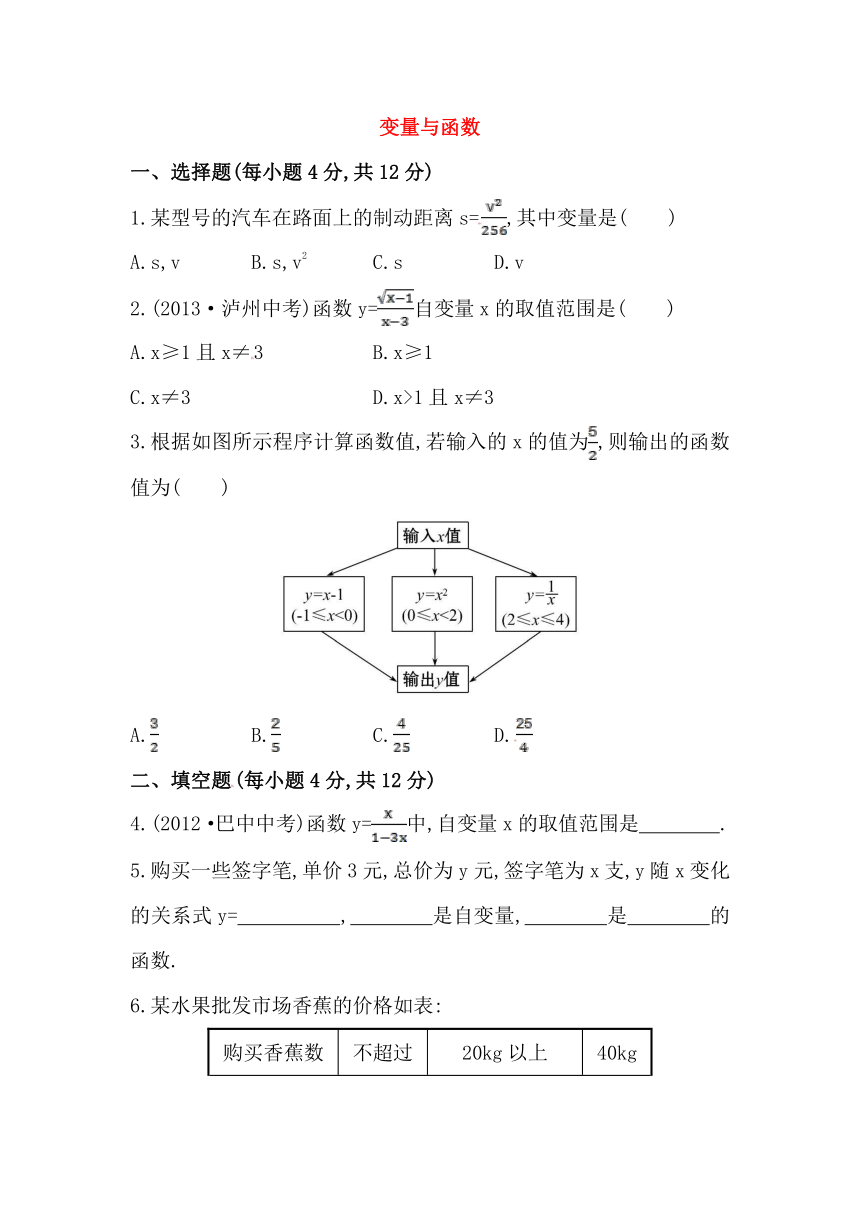
3.根据如图所示程序计算函数值,若输入的x的值为,则输出的函数值为( )
A. B. C. D.
二、填空题(每小题4分,共12分)
4.(2012·巴中中考)函数y=中,自变量x的取值范围是 .
5.购买一些签字笔,单价3元,总价为y元,签字笔为x支,y随x变化的关系式y= , 是自变量, 是 的函数.
6.某水果批发市场香蕉的价格如表:
购买香蕉数(kg) 不超过20kg 20kg以上但不超过40kg 40kg以上
每kg价格 8元 7元 6元
若小强购买香蕉xkg(x大于40kg)付了y元,则y关于x的函数解析式为 .(写出自变量的取值范围)
三、解答题(共26分)
7.(8分)下表给出了橘农王林去年橘子的销售额y(元)随橘子卖出质量x(kg)的变化的有关数据:
卖出质量(kg) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)上表反映了哪两个变量之间的关系 并写出函数的解析式.
(2)哪个是自变量 哪个是自变量的函数
(3)当橘子卖出5kg时,销售额是多少
(4)估计当橘子卖出50kg时,销售额是多少
8.(8分)已知一根长为20m的铁丝围成一个长方形,若宽为x,长为y:
(1)求出y关于x的函数解析式.
(2)写出自变量x的取值范围.
(3)求当x=4时所对应的函数值.
【拓展延伸】
9.(10分)如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合,试写出重叠部分面积y(cm2)与线段MA的长度x(cm)之间的函数解析式,并写出自变量的取值范围.
答案解析
1.【解析】选A.∵制动距离s=,∴s随着v的变化而变化,∴变量是s,v.
2.【解析】选A.根据题意得解得x≥1且x≠3.
【归纳整合】求自变量的取值范围的四种情况
(1)整式:其自变量的取值范围是全体实数.
(2)分式:其自变量的取值范围是使得分母不为0的实数.
(3)二次根式:其自变量的取值范围是使得被开方数为非负的实数.
(4)当函数表示实际问题时,自变量的取值必须使实际问题有意义.
3.【解析】选B.∵x=时,2≤x≤4,
∴将x=代入函数y=得y=.
4.【解析】根据题意得,1-3x≠0,解得x≠.
答案:x≠
5.【解析】根据题意,y=3x,x是自变量,y是x的函数.
答案:3x x y x
6.【解析】因为x大于40kg,所以单价为6元,
所以y=6x(x>40).
答案:y=6x(x>40)
7.【解析】(1)表中反映了橘子的卖出质量与销售额之间的关系,解析式为y=2x.
(2)橘子的卖出质量x是自变量,销售额y是卖出质量x的函数.
(3)当橘子卖出5kg时,销售额y=2×5=10(元).
(4)当橘子卖出50kg时,销售额为y=2×50=100(元).
8.【解析】(1)因为铁丝的长为20m,
所以2(x+y)=20,
整理得,y=-x+10.
(2)0(3)当x=4时,y=-4+10=6.
9.【解析】由题意知∠BAC=45°,∠QMA=90°,
故重叠部分为等腰直角三角形,
所以y=x2,自变量的取值范围是0≤x≤10.
一、选择题(每小题4分,共12分)
1.某型号的汽车在路面上的制动距离s=,其中变量是( )
A.s,v B.s,v2 C.s D.v
2.(2013·泸州中考)函数y=自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1
C.x≠3 D.x>1且x≠3
3.根据如图所示程序计算函数值,若输入的x的值为,则输出的函数值为( )
A. B. C. D.
二、填空题(每小题4分,共12分)
4.(2012·巴中中考)函数y=中,自变量x的取值范围是 .
5.购买一些签字笔,单价3元,总价为y元,签字笔为x支,y随x变化的关系式y= , 是自变量, 是 的函数.
6.某水果批发市场香蕉的价格如表:
购买香蕉数(kg) 不超过20kg 20kg以上但不超过40kg 40kg以上
每kg价格 8元 7元 6元
若小强购买香蕉xkg(x大于40kg)付了y元,则y关于x的函数解析式为 .(写出自变量的取值范围)
三、解答题(共26分)
7.(8分)下表给出了橘农王林去年橘子的销售额y(元)随橘子卖出质量x(kg)的变化的有关数据:
卖出质量(kg) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)上表反映了哪两个变量之间的关系 并写出函数的解析式.
(2)哪个是自变量 哪个是自变量的函数
(3)当橘子卖出5kg时,销售额是多少
(4)估计当橘子卖出50kg时,销售额是多少
8.(8分)已知一根长为20m的铁丝围成一个长方形,若宽为x,长为y:
(1)求出y关于x的函数解析式.
(2)写出自变量x的取值范围.
(3)求当x=4时所对应的函数值.
【拓展延伸】
9.(10分)如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC向右移动,最后让点A与点N重合,试写出重叠部分面积y(cm2)与线段MA的长度x(cm)之间的函数解析式,并写出自变量的取值范围.
答案解析
1.【解析】选A.∵制动距离s=,∴s随着v的变化而变化,∴变量是s,v.
2.【解析】选A.根据题意得解得x≥1且x≠3.
【归纳整合】求自变量的取值范围的四种情况
(1)整式:其自变量的取值范围是全体实数.
(2)分式:其自变量的取值范围是使得分母不为0的实数.
(3)二次根式:其自变量的取值范围是使得被开方数为非负的实数.
(4)当函数表示实际问题时,自变量的取值必须使实际问题有意义.
3.【解析】选B.∵x=时,2≤x≤4,
∴将x=代入函数y=得y=.
4.【解析】根据题意得,1-3x≠0,解得x≠.
答案:x≠
5.【解析】根据题意,y=3x,x是自变量,y是x的函数.
答案:3x x y x
6.【解析】因为x大于40kg,所以单价为6元,
所以y=6x(x>40).
答案:y=6x(x>40)
7.【解析】(1)表中反映了橘子的卖出质量与销售额之间的关系,解析式为y=2x.
(2)橘子的卖出质量x是自变量,销售额y是卖出质量x的函数.
(3)当橘子卖出5kg时,销售额y=2×5=10(元).
(4)当橘子卖出50kg时,销售额为y=2×50=100(元).
8.【解析】(1)因为铁丝的长为20m,
所以2(x+y)=20,
整理得,y=-x+10.
(2)0
9.【解析】由题意知∠BAC=45°,∠QMA=90°,
故重叠部分为等腰直角三角形,
所以y=x2,自变量的取值范围是0≤x≤10.
