广西 等比数列的前n项和2[上学期]
文档属性
| 名称 | 广西 等比数列的前n项和2[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 66.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-19 00:00:00 | ||
图片预览





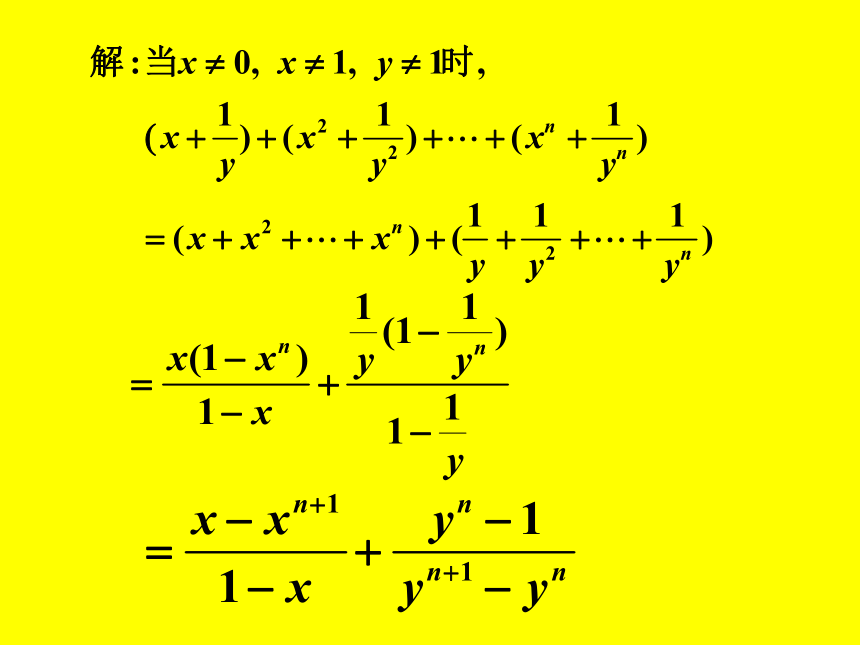
文档简介
课件12张PPT。等比数列的前n项和一、复习:
1.等比数列通项公式:2.等比数列前n项和公式:注意:分q=1和q≠1讨论3.等比数列前 项和公式推导
思想方法:错位相减求和法例2:某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1 年起,约几年内可使总销售量达到30000台(保留到个位)?解:a1=5000, q=1+10%=1.1 sn=30000分析 : 拆项后构成两个等比数列的和的问题, 这样问题就变得容易解决了 .例3. 求和练习:
求和:1+(1/ a)+(1/a2)+……+(1/an)
解:当a≠1时1,1/a,1/a2……1/an构成等比数列且公比q ≠1当a=1时Sn+1=1+(1/1)+(1/12)+……+(1/1n)=n+1 ∴ Sn=n+1a=1a≠1二、新学:例: 在等比数列{an}中,
已知Sn=48,S2n=60,则S3n=____性质1:若等比数列{an}的前n项和为Sn
则 SK, S2K- SK, S3K- S2K也成等比数列1.等比数列前n项和的性质63练习:
若某等比数列中前7项和为48,
前14项和为60,前21项的和为( )
(A)180 (B)108(C)75 (D)63性质2:若等比数列{an}共2n项
则例: 等比数列{an}的项数是偶数,
其各项和为 -240,且奇数项的和
比偶数项的和大80,则公比q=____2课堂小结1.等比数列前n项和的性质性质1:若等比数列{an}的前n项和为Sn
则 Sk, S2k- Sk, S3k- S2k也成等比数列性质2:若等比数列{an}共2n项
则
1.等比数列通项公式:2.等比数列前n项和公式:注意:分q=1和q≠1讨论3.等比数列前 项和公式推导
思想方法:错位相减求和法例2:某商场第1年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从第1 年起,约几年内可使总销售量达到30000台(保留到个位)?解:a1=5000, q=1+10%=1.1 sn=30000分析 : 拆项后构成两个等比数列的和的问题, 这样问题就变得容易解决了 .例3. 求和练习:
求和:1+(1/ a)+(1/a2)+……+(1/an)
解:当a≠1时1,1/a,1/a2……1/an构成等比数列且公比q ≠1当a=1时Sn+1=1+(1/1)+(1/12)+……+(1/1n)=n+1 ∴ Sn=n+1a=1a≠1二、新学:例: 在等比数列{an}中,
已知Sn=48,S2n=60,则S3n=____性质1:若等比数列{an}的前n项和为Sn
则 SK, S2K- SK, S3K- S2K也成等比数列1.等比数列前n项和的性质63练习:
若某等比数列中前7项和为48,
前14项和为60,前21项的和为( )
(A)180 (B)108(C)75 (D)63性质2:若等比数列{an}共2n项
则例: 等比数列{an}的项数是偶数,
其各项和为 -240,且奇数项的和
比偶数项的和大80,则公比q=____2课堂小结1.等比数列前n项和的性质性质1:若等比数列{an}的前n项和为Sn
则 Sk, S2k- Sk, S3k- S2k也成等比数列性质2:若等比数列{an}共2n项
则
