等比数列(2)[上学期]
图片预览




文档简介
课件10张PPT。3.4等比数列(2)铜梁一中 汤贤莲学习目标1.理解并掌握等比数列的性质;
2.灵活应用等比数列的定义,通项公式和性质,
增强应用意识.重点:1.等比数列的性质;
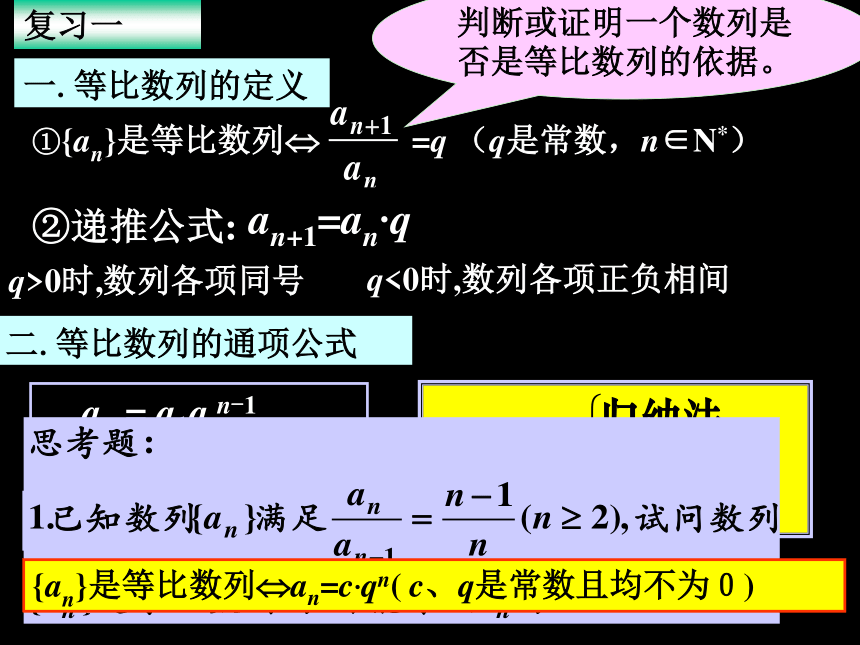
2.等比数列定义,通项公式,性质的应用;难点:知识的灵活应用.教学法:类比教学法.复习一一.等比数列的定义二.等比数列的通项公式an = a1q n-1an = am q n-mq>0时,数列各项同号q<0时,数列各项正负相间①{an}是等比数列? =q (q是常数,n∈N*)判断或证明一个数列是否是等比数列的依据。{an}是等差数列?an=pn+q( p、q是常数){an}是等比数列?an=c·qn( c、q是常数且均不为0)二.等比中项a、G、b成等比数列,则称G是a与b的等比中项。条件:ab>0 2.若{an}为等差数列,则ak, ak+m, ak+2m, ak+3m,…也是等差数列,其公差为md(d为{an}的公差).1. {an}为等差数列,若m+n=p+q,则am+an= ap+aq.若{an}为等差数列,则a1+an= a2+an-1= a3+an-2= …推论1:{an}为等差数列,若2n=p+q,则2an= ap+aq.推论2:(即:有穷等差数列中,与首末两项等距离的两项和相等).(即:等差数列中,序号成等差数列,相应的项也成等差数列)四. 等差数列的性质3.数列 {an}为等差数列,公差为d,则
Sk,S2k-Sk,S3k-S2k, ‥‥;成等差数列,公差为k2d1.{an}为等比数列,若m+n=p+q,则am·an= ap·aq若{an}为等比数列,则a1·an= a2·an-1= a3·an-2= …推论1:{an}为等比数列,若2n=p+q,则an2= ap·aq.推论2:(即:有穷等比数列中,与首末两项等距离的两项积相等).(即:等比数列中,序号成等差数列,相应的项成等比数列)等比数列的性质1.《教材》P125ex10 2.若{an}为等比数列,则ak, ak+m, ak+2m, ak+3m,…也是等比数列,其公比为qm(q为{an}的公比).3.《教材》P129练习ex43.数列 {an}为等比数列,公比为q,则
Sk,S2k-Sk,S3k-S2k, ‥‥;成等比数列.2.《教材》P124练习ex3典例学习例1:在等比数列{an}中,a5=2,a10=10,
求a15.(用多种方法求解)例2:已知{an}、 {bn}是项数相同的等比数列,
求证: {an·bn}是等比数列.已知{an}是等比数列,若c≠0,则{c·an}是等比数列.变式:已知{an}、 {bn}是项数相同的等比数列,
则(1) {an+bn}是等比数列吗?
(2){c·an}是等比数列吗?
(3){ }是等比数列吗?效果检测1.等比数列{an}中,a13=1,a26=2,求a52.3.在正数组成的等比数列{an}中,a4a5a6=3
则log3a1+log3a2+log3a5+log3a8+log3a9= .2:{an}为等比数列,则下列数列中为等比数列的
有那些?
(1) {an3}, (2){pan}, (3){ } (4){an·an+1}小结 本节课学习了等比数列的性质。学习方法为理解识记,理解成立原因是关键—化归证明,识记主要是提供方向。 作业1、课本P125习题2,3,4,5,7,8
2.灵活应用等比数列的定义,通项公式和性质,
增强应用意识.重点:1.等比数列的性质;
2.等比数列定义,通项公式,性质的应用;难点:知识的灵活应用.教学法:类比教学法.复习一一.等比数列的定义二.等比数列的通项公式an = a1q n-1an = am q n-mq>0时,数列各项同号q<0时,数列各项正负相间①{an}是等比数列? =q (q是常数,n∈N*)判断或证明一个数列是否是等比数列的依据。{an}是等差数列?an=pn+q( p、q是常数){an}是等比数列?an=c·qn( c、q是常数且均不为0)二.等比中项a、G、b成等比数列,则称G是a与b的等比中项。条件:ab>0 2.若{an}为等差数列,则ak, ak+m, ak+2m, ak+3m,…也是等差数列,其公差为md(d为{an}的公差).1. {an}为等差数列,若m+n=p+q,则am+an= ap+aq.若{an}为等差数列,则a1+an= a2+an-1= a3+an-2= …推论1:{an}为等差数列,若2n=p+q,则2an= ap+aq.推论2:(即:有穷等差数列中,与首末两项等距离的两项和相等).(即:等差数列中,序号成等差数列,相应的项也成等差数列)四. 等差数列的性质3.数列 {an}为等差数列,公差为d,则
Sk,S2k-Sk,S3k-S2k, ‥‥;成等差数列,公差为k2d1.{an}为等比数列,若m+n=p+q,则am·an= ap·aq若{an}为等比数列,则a1·an= a2·an-1= a3·an-2= …推论1:{an}为等比数列,若2n=p+q,则an2= ap·aq.推论2:(即:有穷等比数列中,与首末两项等距离的两项积相等).(即:等比数列中,序号成等差数列,相应的项成等比数列)等比数列的性质1.《教材》P125ex10 2.若{an}为等比数列,则ak, ak+m, ak+2m, ak+3m,…也是等比数列,其公比为qm(q为{an}的公比).3.《教材》P129练习ex43.数列 {an}为等比数列,公比为q,则
Sk,S2k-Sk,S3k-S2k, ‥‥;成等比数列.2.《教材》P124练习ex3典例学习例1:在等比数列{an}中,a5=2,a10=10,
求a15.(用多种方法求解)例2:已知{an}、 {bn}是项数相同的等比数列,
求证: {an·bn}是等比数列.已知{an}是等比数列,若c≠0,则{c·an}是等比数列.变式:已知{an}、 {bn}是项数相同的等比数列,
则(1) {an+bn}是等比数列吗?
(2){c·an}是等比数列吗?
(3){ }是等比数列吗?效果检测1.等比数列{an}中,a13=1,a26=2,求a52.3.在正数组成的等比数列{an}中,a4a5a6=3
则log3a1+log3a2+log3a5+log3a8+log3a9= .2:{an}为等比数列,则下列数列中为等比数列的
有那些?
(1) {an3}, (2){pan}, (3){ } (4){an·an+1}小结 本节课学习了等比数列的性质。学习方法为理解识记,理解成立原因是关键—化归证明,识记主要是提供方向。 作业1、课本P125习题2,3,4,5,7,8
