7.2勾股定理 课件

课件15张PPT。7、2勾股定理第7章 实数学习目标一、知识与技能：
能记住勾股定理，会运用勾股定理解决一些与直角三角形有关的实际问题。
二、过程与方法：
经历勾股定理的探索过程，感受数形结合的思想，尝试用多种方法验证勾股定理，体验解决问题策略的多样性。
三、情感、态度与价值观：
通过对勾股定理历史的了解，增强同学们的民族自信心与自豪感，激发学习兴趣。实验与探究
（1）用硬纸片剪8个全等的直角三角形，设每个直角三角形两条直角边分别为a，b，斜边为c。
（2）在纸上画出两个边长均为a+b的正方形；按图7-3?所示的方式，将剪出的4个直角三角形摆放在第一个正方形内；按图7-3?所示的方式，将另外的4个直角三角形摆放在第二个正方形内。
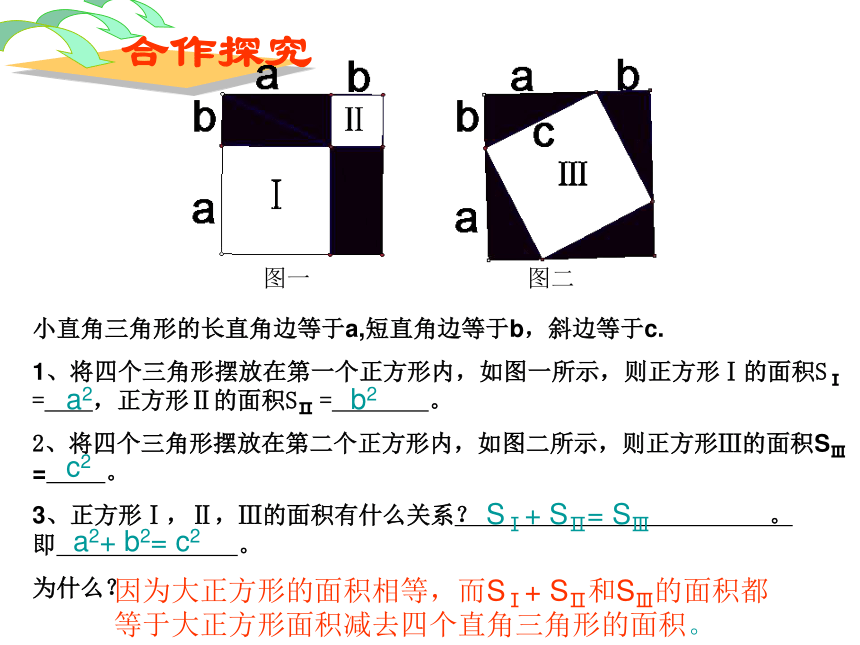
（3）判断图7-3中四边形Ⅰ，Ⅱ，Ⅲ的形状，说出你的理由。小直角三角形的长直角边等于a,短直角边等于b，斜边等于c.
1、将四个三角形摆放在第一个正方形内，如图一所示，则正方形Ⅰ的面积SⅠ = ，正方形Ⅱ的面积SⅡ = 。
2、将四个三角形摆放在第二个正方形内，如图二所示，则正方形Ⅲ的面积SⅢ = 。
3、正方形Ⅰ，Ⅱ，Ⅲ的面积有什么关系？ 。 即 。
为什么？

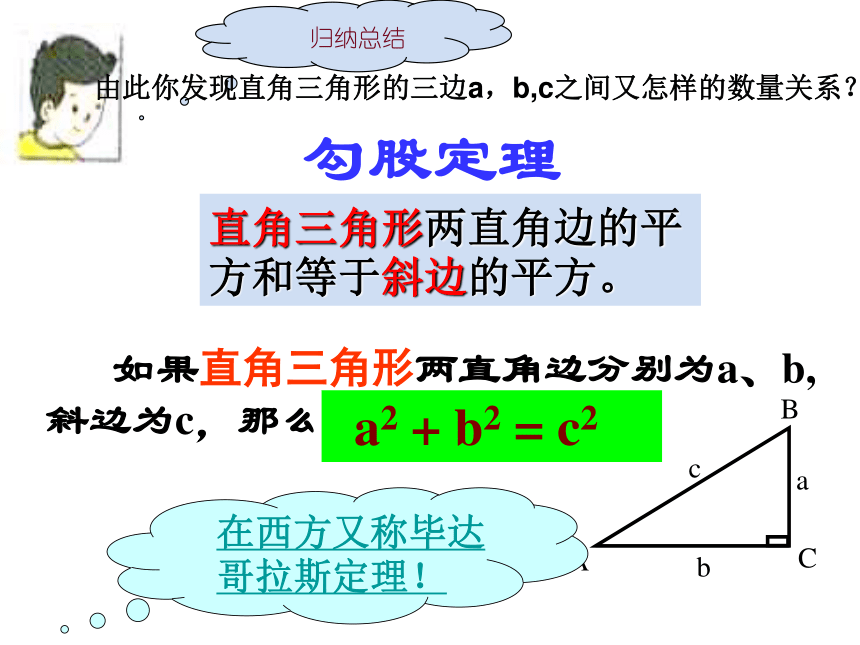
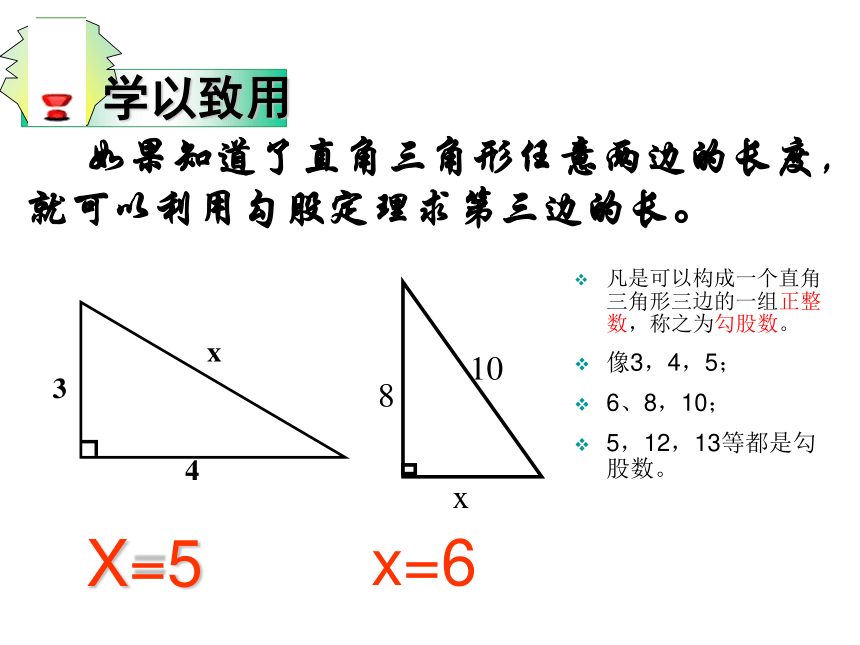
a2b2c2SⅠ+ SⅡ= SⅢa2+ b2= c2因为大正方形的面积相等，而SⅠ+ SⅡ和SⅢ的面积都等于大正方形面积减去四个直角三角形的面积。图一图二归纳总结直角三角形两直角边的平方和等于斜边的平方。 a2 + b2 = c2勾股定理由此你发现直角三角形的三边a，b,c之间又怎样的数量关系？精讲点拨c2=a2+b2a2=c2-b2b2=c2-a2即c=即a=即b===勾股定理揭示了直角三角形三边之间的关系X=5 如果知道了直角三角形任意两边的长度，就可以利用勾股定理求第三边的长。x=6凡是可以构成一个直角三角形三边的一组正整数，称之为勾股数。
像3，4，5；
6、8，10；
5，12，13等都是勾股数。例题学习例1 如图5—2，从电线杆OA的顶端A点，扯
一根钢丝绳固定在地面上的B点，这根钢
丝绳的长度是多少？（AO=8米 BO=6米）BOA连接OB,OB与OA垂直,得直角三角形，在此直角三角形中，已知两直角边求斜边，应该用勾股定理.
分析：明朝程大位的著作《算法統宗》裏有一道“蕩秋千”的趣題，是用詩歌的形式：
平地秋千未起，踏板一尺離地；
送行二步與人齊，五尺人高曾記。
仕女佳人爭蹴，終朝笑語歡嬉；
良工高士好奇，算出索長有幾？趣题欣赏索長有幾例2图1 现代汉语的意思是：有一架秋千，当静止时其踏板离地1尺；将它向前推两步（一步指“双步”，即左右脚各迈一步，一步为5尺）并使秋千的绳索拉直，其踏板离地5尺.求绳索的长.分析：画出如图的图形，由题意可知AC= ；CD= ;CF= .Rt OBF中设OB为x尺，你能解答这个题吗？1尺10尺5尺
解：如图1,设OA为静止时秋千绳索的
长，则
AC=1，CF=5, BF=CD=10. AF=CF-
AC=5-1=4.设
绳索长为OA=OB=x尺。
则 OF=OA-AF=(x-4)尺 在Rt△OBF中，由勾股定理，
得：
OB2=BF2+OF2,即
x2=102+(x-4)2
解得：x=14.5尺
∴绳索长为14.5尺。一、判断题
1. ΔABC的两条边a=6,b=8,则c=10 。 （ ）
2.若直角三角形的两边长为3和4，则第三边为5。 （ ）
3.若a、b、c为直角△ABC的三边,则a2+b2=c2。 （ ）
二、填空题
1、如右图，阴影部分是一个正方形，则此正方形的面积为（ ）。
2、如图，从电线杆的顶端A点，扯一根钢丝绳固定在地面上的B点，这根钢丝绳的长度是（ ） 。
课堂练习×××25B10米 如图,图中所有四边形都是正方形，正方形Ⅰ的边长为7你能求出正方形A、B、C、D的面积之和吗？答案：497拓展延伸abc 小明的妈妈买了一部29英寸（74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你能解释这是为什么吗？∴售货员没搞错∵想一想荧屏对角线大约为74厘米小结说说这节课你有什么收获？探索直角三角形两直角边的平方和等于斜边的平方；
利用勾股定理解决实际问题。 作业习题5.2 A组
T1、2、3