等比数列求和(第一课时)[上学期]
文档属性
| 名称 | 等比数列求和(第一课时)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 22.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-06 17:53:00 | ||
图片预览



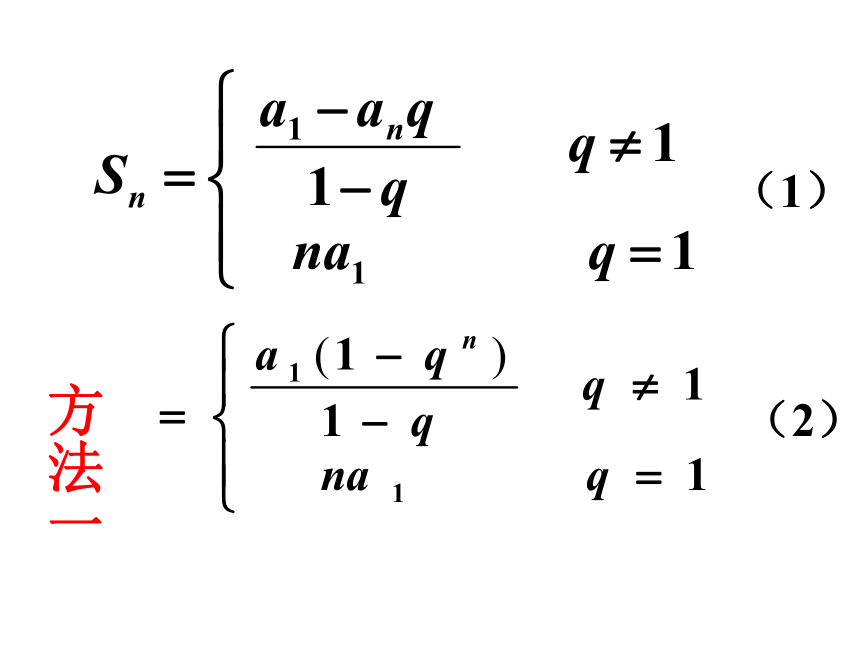


文档简介
课件12张PPT。等比数列的前n项和
(第一课时) 例1、已知a1=3,a2=7且 an+2=3an+1-2an,求通项公式an。 设 bn=an+1-an,
bn=b1·2n-1an=1+2+22+23+······+2n分析:则bn+1/bn=2;
即an+1-an=2n+1一、等比数列的前n项和及公式(1) (2)方法一
Sn=a1 + a2 + a3 + ……+ an=a1+a1q+a2q+······+an-1q=a1+q(a1+a2+······+an-1)=a1+qSn-1=a1+q(Sn-an)∴ (1-q)Sn=a1-anq方法二:Sn=a1 + a2 + a3 + ……+ an=a1+a1q+a1q2+……+a1qn-1 (1) qSn=a1q+a1q2+a1q3+……+a1qn (2)(1-q)Sn=a1(1-qn)方法三:二、应用:练习:书p132Excise:1,2,3.
1、等比数列的前n项和公式:(1)(2)三、小结:2、有关数学思想与方法: (1)、变形思想(包括:合分比、
方程及错位相减等思想);
(2) 、分类思想;(3)、类比思想。四、作业:书p133习题 3.5:1,2,3,4,5,6。例 4、某制糖厂第一年制糖5万
吨,如果平均每年的产量比上
一年增加10%,那么从第一年
起,约几年内可使总产量达到
30万吨(保留到个位)?
(第一课时) 例1、已知a1=3,a2=7且 an+2=3an+1-2an,求通项公式an。 设 bn=an+1-an,
bn=b1·2n-1an=1+2+22+23+······+2n分析:则bn+1/bn=2;
即an+1-an=2n+1一、等比数列的前n项和及公式(1) (2)方法一
Sn=a1 + a2 + a3 + ……+ an=a1+a1q+a2q+······+an-1q=a1+q(a1+a2+······+an-1)=a1+qSn-1=a1+q(Sn-an)∴ (1-q)Sn=a1-anq方法二:Sn=a1 + a2 + a3 + ……+ an=a1+a1q+a1q2+……+a1qn-1 (1) qSn=a1q+a1q2+a1q3+……+a1qn (2)(1-q)Sn=a1(1-qn)方法三:二、应用:练习:书p132Excise:1,2,3.
1、等比数列的前n项和公式:(1)(2)三、小结:2、有关数学思想与方法: (1)、变形思想(包括:合分比、
方程及错位相减等思想);
(2) 、分类思想;(3)、类比思想。四、作业:书p133习题 3.5:1,2,3,4,5,6。例 4、某制糖厂第一年制糖5万
吨,如果平均每年的产量比上
一年增加10%,那么从第一年
起,约几年内可使总产量达到
30万吨(保留到个位)?
