3.1 圆 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
3.1 圆 教学设计
课题 3.1 圆 单元 第2 单元 学科 数学 年级 九年级(下)
教材分析 “圆”是现实世界中常见的图形,是初中几何的最后一章,从整个初中几何的学习来看,它属于“提高阶段”.本节“车轮为什么做成圆形”,主要是让学生通过观察实例归纳出圆的定义,虽然小学阶段学生已经对圆的有关知识有所了解,小学学习圆只是一种感性认识,知道一个图形是圆,但还没有抽象出“平面上到定点的距离等于定长的所有点组成的圆形叫做圆”的概念.本节主要是使学生通过观察实例体会圆的概念的形成过程,进一步归纳出点与圆的三种位置关系.
核心素养分析 从感受圆在生活中大量存在到圆形及圆的形成过程,讲授圆的有关概念.利用操作几何的方法,理解圆是轴对称图形,过圆心的直线都是它的对称轴.经历由生活现象揭示其数学本质的过程,培养抽象思维和归纳概括的能力.
学习目标 1.经历形成圆的概念的过程,经历探索点与圆位置关系的过程.2.理解并掌握与圆有关的概念:弦、直径、半圆、等圆、等弧等.3.结合实例,理解平面内点与圆的三种位置关系.
重点 学会圆、弧、弦等的表示方法,掌握点和圆的位置关系及其判定方法..
难点 学会圆、弧、弦等的表示方法,掌握点和圆的位置关系及其判定方法.
教学过程
教学环节 教师活动 学生活动 设计意图
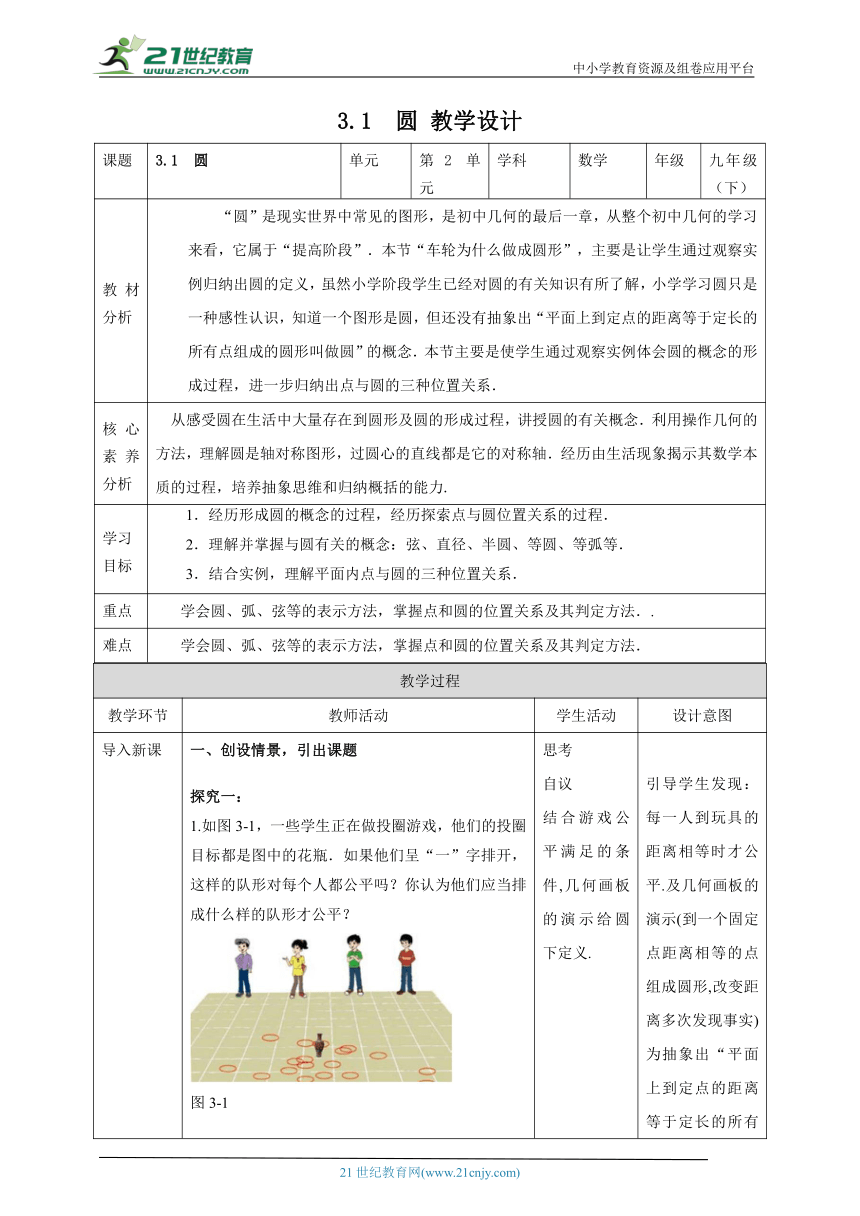
导入新课 一、创设情景,引出课题探究一: 1.如图3-1,一些学生正在做投圈游戏,他们的投圈目标都是图中的花瓶.如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形才公平?图3-1圆还可以看成是到定点的距离等于定长的所有点组成的图形,定点就是圆心,定长就是半径,以点O为圆心的圆记作⊙O,读作“圆 O”。2.确定一个圆需要几个要素?确定圆的要素是:圆心、半径.圆心确定圆的位置,半径确定圆的大小,确定一个圆,两者缺一不可.3.圆的有关概念(1)连接圆上任意两点的线段叫做弦,如图线段AC,AB;(2)经过圆心的弦叫做直径,如图线段AB;(3)圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”读作“圆弧AC”或“弧AC”.大于半圆的弧(如图所示)叫做优弧,小于半圆的弧(如图所示) 或叫做劣弧;圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;(5)能够重合的圆称为等圆;(6)在同圆或等圆中,能够互相重合的弧,称为等弧4.点和圆的位置关系如上图所示,设⊙O的半径为r,点到圆心的距离为d. 则有:点在圆外,d>r;点在圆上,d=r;点在圆内,d<r. 思考自议结合游戏公平满足的条件,几何画板的演示给圆下定义. 引导学生发现:每一人到玩具的距离相等时才公平.及几何画板的演示(到一个固定点距离相等的点组成圆形,改变距离多次发现事实)为抽象出“平面上到定点的距离等于定长的所有点组成的图形叫做圆”的概念做准备.
讲授新课 提炼概念典例精讲 例:已知⊙O 的半径r=5 cm,圆心O 到直线l 的距离d=OD=3 cm, 在直线l 上有P,Q,R 三点, 且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的? 通过探究,使学生理解点与圆的位置关系,并体会定性分析与定量分析的关系. 整个过程为学生提供了充分的从事数学研究和交流的机会,使学生主动观察、讨论、概括得到新知,亲历了“做数学”的过程.
课堂练习 四、巩固训练 1.下列说法中,正确的是( )①弦是直径;②半圆是弧;③过圆心的线段是直径;④半圆是最长的弧;⑤直径是圆中最长的弦.②③ B.③⑤ C.④⑤ D.②⑤ D2.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法不正确的是( ) A.当a<5时,点B在⊙A内 B.当1<a<5时,点B在⊙A内 C.当a<1时,点B在⊙A外 D.当a>5时,点B在⊙A外 C3.一点和⊙O上的最近点距离为4cm,最远的距离为10cm,则这个圆的半径是 .7cm或3cm4.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A .上,外,上5.设AB=3cm,画图说明∶到点A的距离小子2cm,且到点B的距离大于2cm的所有点组成的图形.解:如图,以A,B为圆心,2cm为半径画圆且相交。阴影部分即为符合题意的图形(除去圆周上的部分)6.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.解:∵∠C=90°,AC=4,AB=5,∴BC=3.∵AC=4>r,∴点A在⊙C外.∵BC=3=r,∴点B在⊙C上.7.如图,矩形ABCD中,AB=3,AD=4,连接AC,BD.(1)过点D作DF⊥AC于点F,过点A作AE⊥BD于点E,并求AE,AF的长.(2)以点A为圆心画圆,使B,C,D,E,F这5个点中至少有1个点在圆内,且至少有2个点在圆外,并求⊙A的半径r的取值范围.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
3.1 圆 教学设计
课题 3.1 圆 单元 第2 单元 学科 数学 年级 九年级(下)
教材分析 “圆”是现实世界中常见的图形,是初中几何的最后一章,从整个初中几何的学习来看,它属于“提高阶段”.本节“车轮为什么做成圆形”,主要是让学生通过观察实例归纳出圆的定义,虽然小学阶段学生已经对圆的有关知识有所了解,小学学习圆只是一种感性认识,知道一个图形是圆,但还没有抽象出“平面上到定点的距离等于定长的所有点组成的圆形叫做圆”的概念.本节主要是使学生通过观察实例体会圆的概念的形成过程,进一步归纳出点与圆的三种位置关系.
核心素养分析 从感受圆在生活中大量存在到圆形及圆的形成过程,讲授圆的有关概念.利用操作几何的方法,理解圆是轴对称图形,过圆心的直线都是它的对称轴.经历由生活现象揭示其数学本质的过程,培养抽象思维和归纳概括的能力.
学习目标 1.经历形成圆的概念的过程,经历探索点与圆位置关系的过程.2.理解并掌握与圆有关的概念:弦、直径、半圆、等圆、等弧等.3.结合实例,理解平面内点与圆的三种位置关系.
重点 学会圆、弧、弦等的表示方法,掌握点和圆的位置关系及其判定方法..
难点 学会圆、弧、弦等的表示方法,掌握点和圆的位置关系及其判定方法.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题探究一: 1.如图3-1,一些学生正在做投圈游戏,他们的投圈目标都是图中的花瓶.如果他们呈“一”字排开,这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形才公平?图3-1圆还可以看成是到定点的距离等于定长的所有点组成的图形,定点就是圆心,定长就是半径,以点O为圆心的圆记作⊙O,读作“圆 O”。2.确定一个圆需要几个要素?确定圆的要素是:圆心、半径.圆心确定圆的位置,半径确定圆的大小,确定一个圆,两者缺一不可.3.圆的有关概念(1)连接圆上任意两点的线段叫做弦,如图线段AC,AB;(2)经过圆心的弦叫做直径,如图线段AB;(3)圆上任意两点间的部分叫做圆弧,简称弧,“以A、C为端点的弧记作”读作“圆弧AC”或“弧AC”.大于半圆的弧(如图所示)叫做优弧,小于半圆的弧(如图所示) 或叫做劣弧;圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;(5)能够重合的圆称为等圆;(6)在同圆或等圆中,能够互相重合的弧,称为等弧4.点和圆的位置关系如上图所示,设⊙O的半径为r,点到圆心的距离为d. 则有:点在圆外,d>r;点在圆上,d=r;点在圆内,d<r. 思考自议结合游戏公平满足的条件,几何画板的演示给圆下定义. 引导学生发现:每一人到玩具的距离相等时才公平.及几何画板的演示(到一个固定点距离相等的点组成圆形,改变距离多次发现事实)为抽象出“平面上到定点的距离等于定长的所有点组成的图形叫做圆”的概念做准备.
讲授新课 提炼概念典例精讲 例:已知⊙O 的半径r=5 cm,圆心O 到直线l 的距离d=OD=3 cm, 在直线l 上有P,Q,R 三点, 且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R 三点与⊙ O 的位置关系各是怎样的? 通过探究,使学生理解点与圆的位置关系,并体会定性分析与定量分析的关系. 整个过程为学生提供了充分的从事数学研究和交流的机会,使学生主动观察、讨论、概括得到新知,亲历了“做数学”的过程.
课堂练习 四、巩固训练 1.下列说法中,正确的是( )①弦是直径;②半圆是弧;③过圆心的线段是直径;④半圆是最长的弧;⑤直径是圆中最长的弦.②③ B.③⑤ C.④⑤ D.②⑤ D2.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法不正确的是( ) A.当a<5时,点B在⊙A内 B.当1<a<5时,点B在⊙A内 C.当a<1时,点B在⊙A外 D.当a>5时,点B在⊙A外 C3.一点和⊙O上的最近点距离为4cm,最远的距离为10cm,则这个圆的半径是 .7cm或3cm4.正方形ABCD的边长为2cm,以A为圆心,2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A .上,外,上5.设AB=3cm,画图说明∶到点A的距离小子2cm,且到点B的距离大于2cm的所有点组成的图形.解:如图,以A,B为圆心,2cm为半径画圆且相交。阴影部分即为符合题意的图形(除去圆周上的部分)6.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,r=3为半径作圆,判断A,B两点和⊙C的位置关系.解:∵∠C=90°,AC=4,AB=5,∴BC=3.∵AC=4>r,∴点A在⊙C外.∵BC=3=r,∴点B在⊙C上.7.如图,矩形ABCD中,AB=3,AD=4,连接AC,BD.(1)过点D作DF⊥AC于点F,过点A作AE⊥BD于点E,并求AE,AF的长.(2)以点A为圆心画圆,使B,C,D,E,F这5个点中至少有1个点在圆内,且至少有2个点在圆外,并求⊙A的半径r的取值范围.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
