等差数列的前n项和[上学期]
图片预览





文档简介
课件13张PPT。高一数学第三章
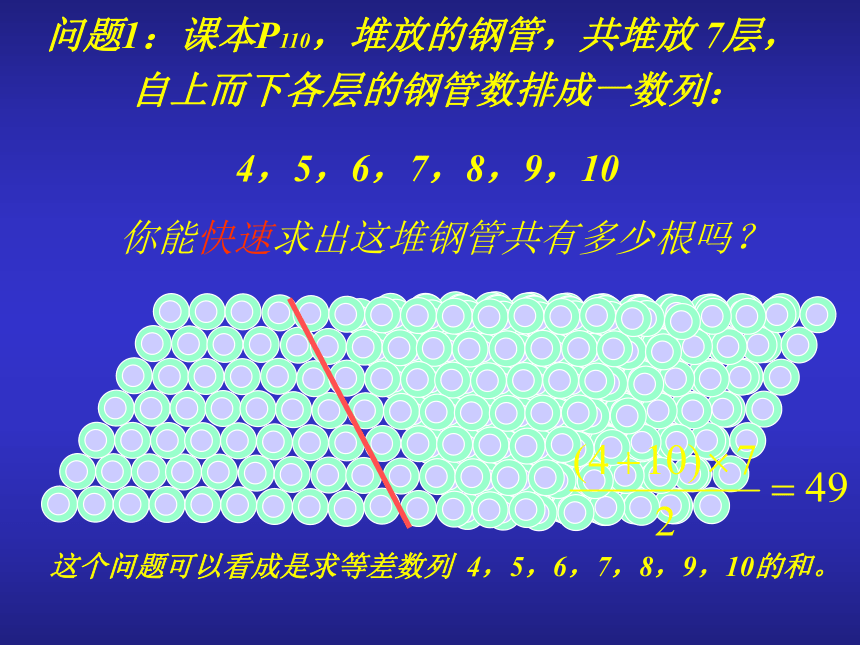
3.3 等差数列的前n项和 问题1:课本P110,堆放的钢管,共堆放 7层, 自上而下各层的钢管数排成一数列:
4,5,6,7,8,9,10你能快速求出这堆钢管共有多少根吗?这个问题可以看成是求等差数列 4,5,6,7,8,9,10的和。问题2:1+2+3+…+100=? 这个问题,德国著名数学家高斯(1777年—1855年)10岁时曾很快求出它的结果。(你知道应如何算吗?)高斯的算法是:
首项与末项的和:1+100=101,
第2 项与倒数第2 项的和:2+99=101,
第3 项与倒数第3项的和:3+98=101,
……
第50项与倒数第50项的和:50+51=101,
于是所求的和是: 这个问题,可看成是求等差数列 1,2,3,…,n,…的前100项的和。根据等差数列的定义,上式用a1和d可写成:
Sn=a1+(a1+d)+···+[a1+(n-1)d] ①把项的次序反过来,Sn又可用an和d表示成:
Sn=an+(an-d)+···+[an-(n-1)d] ②把①、②两边分别相加,得:等差数列前n项的和即 Sn= a1+a2+…+ an设等差数列 {an}前n项的和为Sn=n(a1+an)由此得到等差数列的{an}前n项和的公式即:等差数列前n项的和等于首末项的和与项数乘积的一半。上面的公式又可以写成 两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。例1:在等差数列{an}中,(2)a1=14.5,d=0.7,an=32,求Sn(1)a3= -2,a8=12,求S10解:(1)?a1+a10 = a3+a8 = 10例2 如图,一个堆放铅笔的 V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解:由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,记为{an},其中 a1=1 , a120=120.根据等差数列前n项和的公式,得答:V形架上共放着 7 260支铅笔。例3 等差数列 -10,-6,-2,2,…前多少项的和是54?例4 已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗? 这就是说,已知 S10与 S20 可以确定这个数列的前n项的和的公式,这个公式是小 结:1、等差数列的求和公式:2、推导等差数列的求和公式的方法:倒序求和法(亦称高斯法)巩固练习1、已知 a6+a9+a12+a15=192,求 S202、凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时,a9=180 o,不合题意,故选(B)BCa1=1100 3、有30根水泥电线杆,要运往1000m处放一根,以后每50m放一根,一辆汽车每次只能运三根,如果用一辆汽车完成这项任务,这辆汽车的行程共有多少千米。MAB解:如图,假定30根电线杆均在点M处, 由于一辆汽车每次只能装3根,所以每次运输只能到达 C、F… 这些地方,这样组成公差为 150、首项为 1100的等差数列,再考虑往返,所以行程共35.5 kmDEF1000a2=12505050505050作 业课 本 P122 第1、2、3、4题2000年12月27日
3.3 等差数列的前n项和 问题1:课本P110,堆放的钢管,共堆放 7层, 自上而下各层的钢管数排成一数列:
4,5,6,7,8,9,10你能快速求出这堆钢管共有多少根吗?这个问题可以看成是求等差数列 4,5,6,7,8,9,10的和。问题2:1+2+3+…+100=? 这个问题,德国著名数学家高斯(1777年—1855年)10岁时曾很快求出它的结果。(你知道应如何算吗?)高斯的算法是:
首项与末项的和:1+100=101,
第2 项与倒数第2 项的和:2+99=101,
第3 项与倒数第3项的和:3+98=101,
……
第50项与倒数第50项的和:50+51=101,
于是所求的和是: 这个问题,可看成是求等差数列 1,2,3,…,n,…的前100项的和。根据等差数列的定义,上式用a1和d可写成:
Sn=a1+(a1+d)+···+[a1+(n-1)d] ①把项的次序反过来,Sn又可用an和d表示成:
Sn=an+(an-d)+···+[an-(n-1)d] ②把①、②两边分别相加,得:等差数列前n项的和即 Sn= a1+a2+…+ an设等差数列 {an}前n项的和为Sn=n(a1+an)由此得到等差数列的{an}前n项和的公式即:等差数列前n项的和等于首末项的和与项数乘积的一半。上面的公式又可以写成 两个公式的共同点是需知 a1和 n,不同点是前者还需知 an,后者还需知 d,解题时需根据已知条件决定选用哪个公式。例1:在等差数列{an}中,(2)a1=14.5,d=0.7,an=32,求Sn(1)a3= -2,a8=12,求S10解:(1)?a1+a10 = a3+a8 = 10例2 如图,一个堆放铅笔的 V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解:由题意可知,这个V形架上共放着120层铅笔,且自下而上各层的铅笔数成等差数列,记为{an},其中 a1=1 , a120=120.根据等差数列前n项和的公式,得答:V形架上共放着 7 260支铅笔。例3 等差数列 -10,-6,-2,2,…前多少项的和是54?例4 已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗? 这就是说,已知 S10与 S20 可以确定这个数列的前n项的和的公式,这个公式是小 结:1、等差数列的求和公式:2、推导等差数列的求和公式的方法:倒序求和法(亦称高斯法)巩固练习1、已知 a6+a9+a12+a15=192,求 S202、凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时,a9=180 o,不合题意,故选(B)BCa1=1100 3、有30根水泥电线杆,要运往1000m处放一根,以后每50m放一根,一辆汽车每次只能运三根,如果用一辆汽车完成这项任务,这辆汽车的行程共有多少千米。MAB解:如图,假定30根电线杆均在点M处, 由于一辆汽车每次只能装3根,所以每次运输只能到达 C、F… 这些地方,这样组成公差为 150、首项为 1100的等差数列,再考虑往返,所以行程共35.5 kmDEF1000a2=12505050505050作 业课 本 P122 第1、2、3、4题2000年12月27日
