等差数列[上学期]
图片预览






文档简介
(共20张PPT)
等差数列
新疆奎屯市一中 王新敞
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。
数列中的每一个数叫做这个数列的项。
数列中的各项依次叫做这个数列的
第1项(或首项)用 表示,
第2项用 表示,
…,
第n项用 表示,
…,
数列的一般形式可以写成:
…,
…,
简记作:
复习数列的有关概念2
如果数列 的第n项 与n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式。
叫做数列 的前n项和。
等差数列的有关概念
观察数列 ( 1) 4,5,6,7,8,9,10.
(2) 1,4,7,10,13,16,…
(3) 7x, 3x,-x,-5x,-9x,…
(4) 2,0,-2,-4,-6,…
(5) 5,5,5,5,5,5,…
(6) 0,0,0,0,0,…
定义:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数(指与n无关的数),这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。
以上6个数列的公差分别为…
公差 d=1 递增数列
公差 d=3 递增数列
公差 d= -4x
公差 d= -2 递减数列
公差 d=0 非零常数列
公差 d=0 零常数列
因为x的正负性不确定,所以该数列的增减性尚不能确定。
等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…,
由此可知,等差数列 的通项公式为
当d≠0时,这是关于n的一个一次函数。
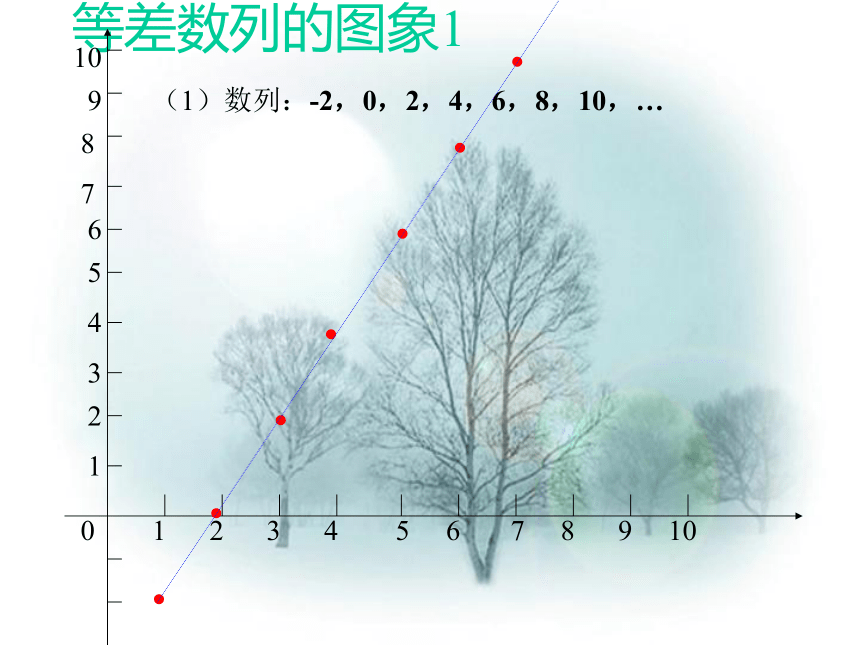
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
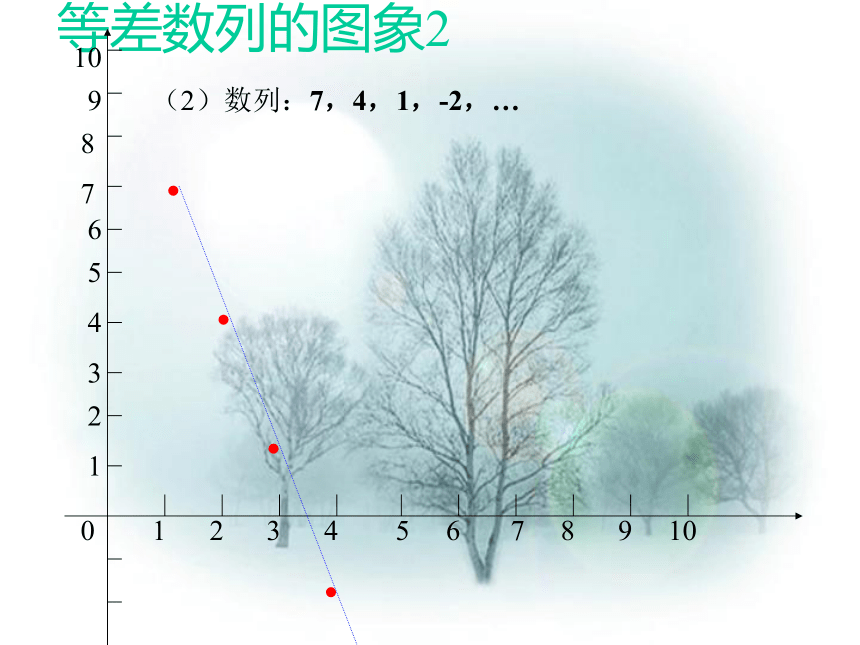
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
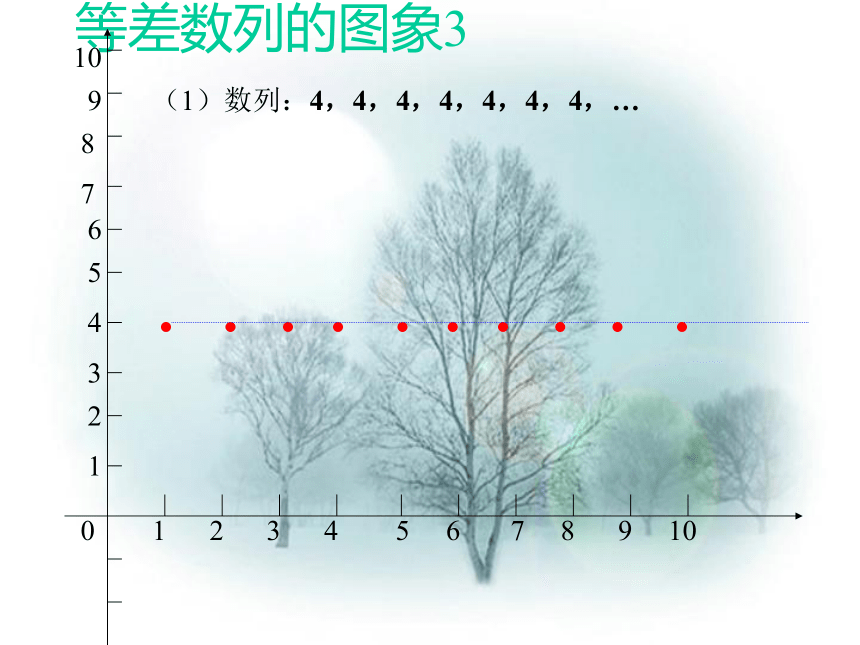
等差数列的图象3
(1)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
等差中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等差数列:
(1)2 , , 4 (2)-1, ,5
(3)-12, ,0 (4)0, ,0
3
2
-6
0
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
等差数列的的例题1-2
例1 求等差数列8,5,2,…,的第20项。
解:
例2 等差数列 -5,-9,-13,…,的第几项是 –401?
解:
因此,
解得
答:这个数列的第100项是-401.
等差数列的的例题3
例3 梯子的最高一级宽33cm,最低一级宽110cm,中间还有10级.计算中间各级的宽.
解:
用 表示题中的等差数列,由已知条件,有
即 110=33+11d,
解得 d=7
因此,
答:梯子中间各级的宽从上到下依次是
40cm,
47cm,
54cm,
61cm,
68cm,
75cm,
82cm,
89cm,
96cm,
103cm.
等差数列的的练习1
1. 求等差数列3,7,11,…的第4,7,10项;
2. 求等差数列10,8,6,…的第20项;
3. 求等差数列2,9,16,…的第n项;
4. 求等差数列0,-7/2,-7…的第n+1项;
等差数列的前n项和公式的推导
…,
…,
由等差数列
的前n项和
得
等差数列的前n项和公式的其它形式
等差数列的的例题4
例4 一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支. 这个V形架上共放着多少支铅笔?
解:由题意可知,这个V形架上共放着120层铅笔,
且自下而上各层的铅笔数组成等差数列,记为
答:V形架上共放着7260支铅笔.
等差数列的的例题5
例5 求集合 的元素个数,并求这些元素的和.
解:
所以集合M中的元素共有14个.
将它们从小到大列出,得
即 7,14,21,28,…,98
这个数列是成等差数列,记为
答:集合M共有14个元素,它们的和等于735.
等差数列的的例题6
例6 已知一个直角三角形的三条边的长成等差数列,求证它们的比是3:4:5.
证明:
将成等差数列的三条边的长从小到大排列,
它们可以表示为
a-d, a, a+d (这里a-d>0,d>0)
由勾股定理,得到
解得
从而这三边的长是
3d,
4d,
5d,
因此,这三条边的长的比是3:4:5
等差数列的的练习2
2. 根据下列条件,求相应的等差数列 的
等差数列的的练习3-4
3. 求自然数中前n个数的和.
4. 求自然数中前n个偶数的和.
等差数列的的作业
祝同学们学习愉快,人人成绩优异!
等差数列
新疆奎屯市一中 王新敞
复习数列的有关概念1
按一定的次序排列的一列数叫做数列。
数列中的每一个数叫做这个数列的项。
数列中的各项依次叫做这个数列的
第1项(或首项)用 表示,
第2项用 表示,
…,
第n项用 表示,
…,
数列的一般形式可以写成:
…,
…,
简记作:
复习数列的有关概念2
如果数列 的第n项 与n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式。
叫做数列 的前n项和。
等差数列的有关概念
观察数列 ( 1) 4,5,6,7,8,9,10.
(2) 1,4,7,10,13,16,…
(3) 7x, 3x,-x,-5x,-9x,…
(4) 2,0,-2,-4,-6,…
(5) 5,5,5,5,5,5,…
(6) 0,0,0,0,0,…
定义:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数(指与n无关的数),这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。
以上6个数列的公差分别为…
公差 d=1 递增数列
公差 d=3 递增数列
公差 d= -4x
公差 d= -2 递减数列
公差 d=0 非零常数列
公差 d=0 零常数列
因为x的正负性不确定,所以该数列的增减性尚不能确定。
等差数列的通项公式
如果一个数列
是等差数列,它的公差是d,那么
…,
…,
由此可知,等差数列 的通项公式为
当d≠0时,这是关于n的一个一次函数。
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
等差数列的图象3
(1)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
等差中项
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等差数列:
(1)2 , , 4 (2)-1, ,5
(3)-12, ,0 (4)0, ,0
3
2
-6
0
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
等差数列的的例题1-2
例1 求等差数列8,5,2,…,的第20项。
解:
例2 等差数列 -5,-9,-13,…,的第几项是 –401?
解:
因此,
解得
答:这个数列的第100项是-401.
等差数列的的例题3
例3 梯子的最高一级宽33cm,最低一级宽110cm,中间还有10级.计算中间各级的宽.
解:
用 表示题中的等差数列,由已知条件,有
即 110=33+11d,
解得 d=7
因此,
答:梯子中间各级的宽从上到下依次是
40cm,
47cm,
54cm,
61cm,
68cm,
75cm,
82cm,
89cm,
96cm,
103cm.
等差数列的的练习1
1. 求等差数列3,7,11,…的第4,7,10项;
2. 求等差数列10,8,6,…的第20项;
3. 求等差数列2,9,16,…的第n项;
4. 求等差数列0,-7/2,-7…的第n+1项;
等差数列的前n项和公式的推导
…,
…,
由等差数列
的前n项和
得
等差数列的前n项和公式的其它形式
等差数列的的例题4
例4 一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放120支. 这个V形架上共放着多少支铅笔?
解:由题意可知,这个V形架上共放着120层铅笔,
且自下而上各层的铅笔数组成等差数列,记为
答:V形架上共放着7260支铅笔.
等差数列的的例题5
例5 求集合 的元素个数,并求这些元素的和.
解:
所以集合M中的元素共有14个.
将它们从小到大列出,得
即 7,14,21,28,…,98
这个数列是成等差数列,记为
答:集合M共有14个元素,它们的和等于735.
等差数列的的例题6
例6 已知一个直角三角形的三条边的长成等差数列,求证它们的比是3:4:5.
证明:
将成等差数列的三条边的长从小到大排列,
它们可以表示为
a-d, a, a+d (这里a-d>0,d>0)
由勾股定理,得到
解得
从而这三边的长是
3d,
4d,
5d,
因此,这三条边的长的比是3:4:5
等差数列的的练习2
2. 根据下列条件,求相应的等差数列 的
等差数列的的练习3-4
3. 求自然数中前n个数的和.
4. 求自然数中前n个偶数的和.
等差数列的的作业
祝同学们学习愉快,人人成绩优异!
