正弦定理[下学期]
图片预览





文档简介
课件14张PPT。5.9.1 正弦定理5.9 正弦定理、余弦定理
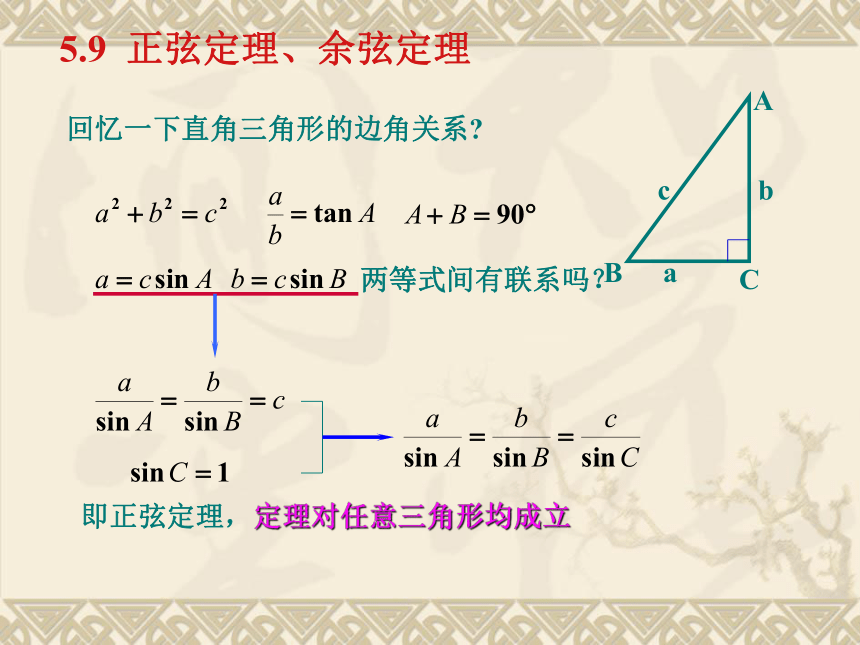
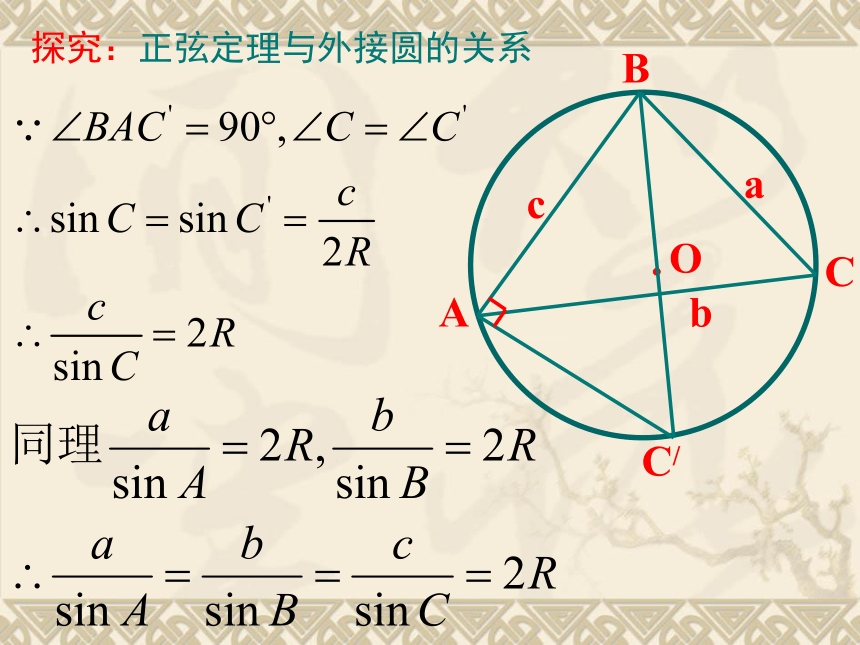
两等式间有联系吗?即正弦定理,定理对任意三角形均成立文字表述正弦定理即:?在一个三角形中,各边和它所对角的正弦的比值相等。正弦定理正弦定理是直角三角形边角关系的一个推广。说明(1)正弦定理对任意三角形都成立;它揭示了三角形中边与角的一种关系。 (2)正弦定理的几种变式:(类同比例的性质)探究:该比值是什么?探究:正弦定理与外接圆的关系正弦定理的应用(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他 的边和角)知 “三” 求 “三”解:∵正弦定理应用一:
已知两角和任意一边,求其余两边和一角案例探究例⒉在△ABC中,已知a=2,b= ,A=45°,
求B和c。变式1:在△ABC中,已知a=4,b= ,A=45°,
求B和c。变式2:在△ABC中,已知a= ,b= ,A=45°,
求B和c。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解或无解)
(1)A为锐角=(一解)(两解)(一解)案例小结!(2)A为直角或钝角a>b(一解)a>b(一解)例题讲解 例3 在 中, ,求
的面积S. 解:∴由正弦定理得 练习:(1)在 中,一定成立的等式是( ) C(2)在 中,若 ,则 是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三有形D练习:(3)在任一 中,求证: 证明:由于正弦定理:令 ∴ 等式成立.课时小结:(1)通过本节学习,我们研究了正弦定理的证明方法,同时了解了向量工具的作用.(2)明确了利用正弦定理解决两类有关三角形问题.(3)已知两边和其中一边所对的角;两角一边.课后作业:(一)课本习题 5.9 1、2在作业本;3、4在练习本(二)预习课本第142—143页余弦定理课后反思: 本节学习旨在掌握正弦定理、定理的推导和应用,通过对例题的学习,能掌握用正弦定理解决两类问题.
三种 ——等积法 分割法 向量法定理思想方法 小结提高二种 —— 转化思想 方程思想
两等式间有联系吗?即正弦定理,定理对任意三角形均成立文字表述正弦定理即:?在一个三角形中,各边和它所对角的正弦的比值相等。正弦定理正弦定理是直角三角形边角关系的一个推广。说明(1)正弦定理对任意三角形都成立;它揭示了三角形中边与角的一种关系。 (2)正弦定理的几种变式:(类同比例的性质)探究:该比值是什么?探究:正弦定理与外接圆的关系正弦定理的应用(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他 的边和角)知 “三” 求 “三”解:∵正弦定理应用一:
已知两角和任意一边,求其余两边和一角案例探究例⒉在△ABC中,已知a=2,b= ,A=45°,
求B和c。变式1:在△ABC中,已知a=4,b= ,A=45°,
求B和c。变式2:在△ABC中,已知a= ,b= ,A=45°,
求B和c。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解或无解)
(1)A为锐角=(一解)(两解)(一解)案例小结!(2)A为直角或钝角a>b(一解)a>b(一解)例题讲解 例3 在 中, ,求
的面积S. 解:∴由正弦定理得 练习:(1)在 中,一定成立的等式是( ) C(2)在 中,若 ,则 是( )
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等边三有形D练习:(3)在任一 中,求证: 证明:由于正弦定理:令 ∴ 等式成立.课时小结:(1)通过本节学习,我们研究了正弦定理的证明方法,同时了解了向量工具的作用.(2)明确了利用正弦定理解决两类有关三角形问题.(3)已知两边和其中一边所对的角;两角一边.课后作业:(一)课本习题 5.9 1、2在作业本;3、4在练习本(二)预习课本第142—143页余弦定理课后反思: 本节学习旨在掌握正弦定理、定理的推导和应用,通过对例题的学习,能掌握用正弦定理解决两类问题.
三种 ——等积法 分割法 向量法定理思想方法 小结提高二种 —— 转化思想 方程思想
