正弦定理

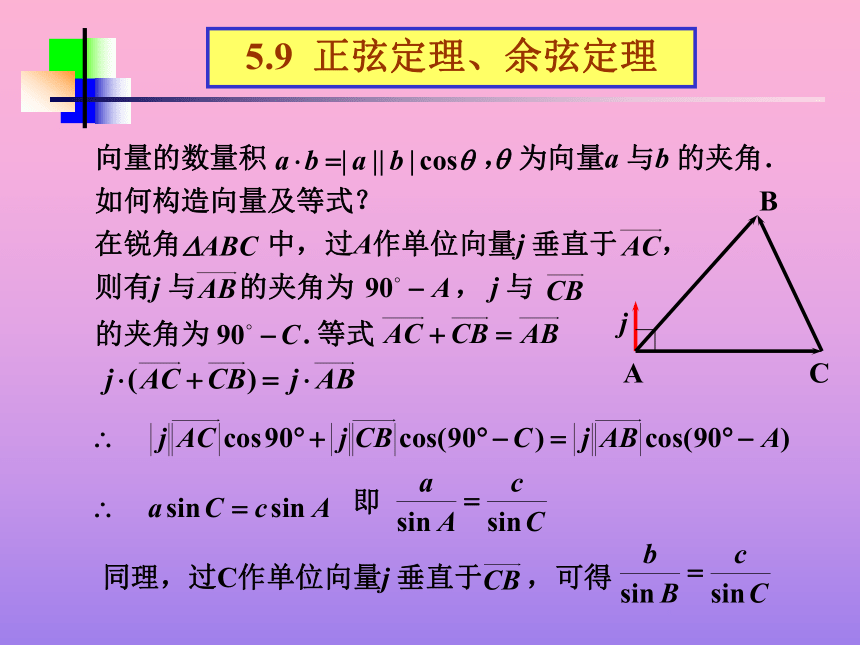
课件10张PPT。5.9 正弦定理、余弦定理D5.9 正弦定理、余弦定理两等式间有联系吗？即正弦定理，定理对任意三角形均成立．利用向量如何在三角形的边长与三角函数建立联系？5.9 正弦定理、余弦定理向量的数量积 ， 为向量a 与b 的夹角． 如何构造向量及等式？则有j 与 的夹角为 ， j 与
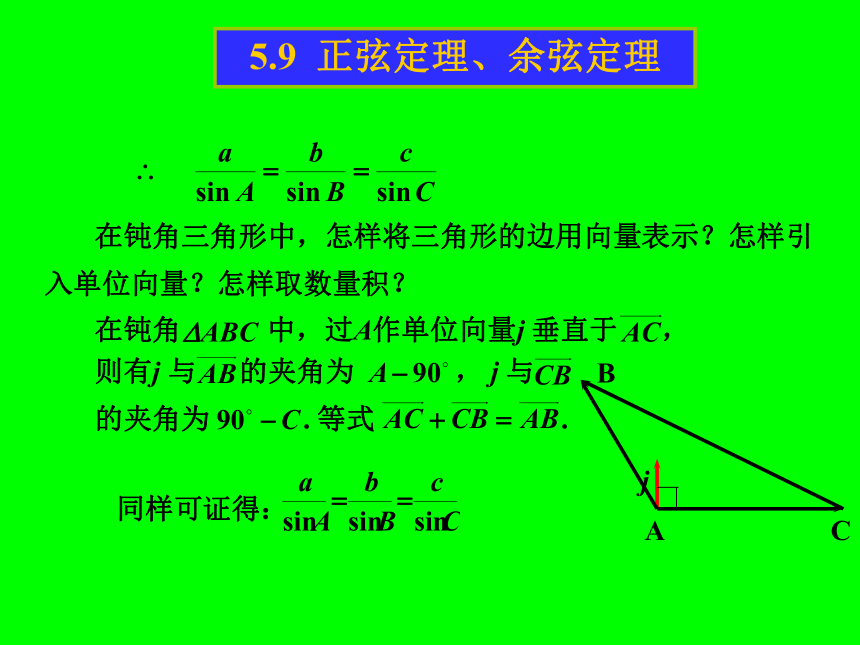
的夹角为 . 等式怎样建立三角形中边和角间的关系？即同理，过C作单位向量j 垂直于 ，可得5.9 正弦定理、余弦定理 在钝角三角形中，怎样将三角形的边用向量表示？怎样引
入单位向量？怎样取数量积？同样可证得：5.9 正弦定理、余弦定理正弦定理可以解什么类型的三角形问题？ 已知两角和任意一边，可以求出其他两边和一角；已知两
边和其中一边的对角，可以求出三角形的其他的边和角。
5.9 正弦定理、余弦定理例题讲解 例1 在 中，已知 ，求b（保
留两个有效数字）. 解：∵ 且5.9 正弦定理、余弦定理例2 在 中，已知 ，求 。例题讲解解：由 得 ∵ 在 中 ∴ A 为锐角 5.9 正弦定理、余弦定理例题讲解 例3 在 中， ，求
的面积S． ∴由正弦定理得 5.9 正弦定理、余弦定理练习：（1）在 中，一定成立的等式是（ ） C（2）在 中，若 ，则 是( )
A．等腰三角形 B．等腰直角三角形
C．直角三角形 D．等边三有形D5.9 正弦定理、余弦定理练习：（3）在任一 中，求证： 证明：由于正弦定理：令 ∴ 等式成立=右边