5.3.2 命题、定理、证明 同步练习(含答案) 2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 5.3.2 命题、定理、证明 同步练习(含答案) 2022-2023学年人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1001.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 00:00:00 | ||
图片预览



文档简介
5.3.2 命题、定理、证明
同步练习
一、选择题.
1. 下列语句中,是命题的是( )
A. 两个相等的角是对顶角 B. 在直线上任取一点
C. 用量角器量角的度数 D. 直角都相等吗?
2. 下列说法中,正确的是( )
A. “同位角相等”是一个真命题
B. 图形的平移是指把图形沿水平方向移动
C. “凡直角都相等”是一个假命题
D. 在平移的过程中,对应线段互相平行或在同一条直线上且相等
3. 下列命题中,是假命题的是( )
A. 对顶角相等 B. 两直线平行,同旁内角互补
C. 和度的两个角是邻补角 D. 垂线段最短
4. 下列命题中,真命题的个数是( )
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
两条直线被第三条直线所截,同旁内角互补
两直线平行,内错角相等
同一平面内,过一点有且只有一条直线与已知直线垂直
从直线外一点到这条直线的垂线段,叫做这点到直线的距离
A. 个 B. 个 C. 个 D. 个
5. 下列命题中,是真命题的有( )
同位角相等对顶角相等同一平面内,如果直线,直线,那么同一平面内,如果直线,直线,那么.
A. 个 B. 个 C. 个 D. 个
6. 下列语句中,是命题的是( )
若,,则;内错角相等吗?
画线段;如果,,那么;直角都相等
A. B. C. D.
7. 对假命题“任何一个角的补角都不小于这个角”举反例,下列选项中,正确的是( )
A. ,的补角,
B. ,的补角,
C. ,的补角,
D. 互为邻补角的两个角
8. 能说明“锐角,锐角的和是锐角”是假命题的例证图是( )
A. B.
C. D.
二、填空题.
9. 命题“对顶角相等”的题设是 .
10. “对顶角相等”是一个______命题填“真”或“假”.
11. 已知命题:如果,那么;如果,那么;等角的余角相等;两个相等的角是对顶角.其中是假命题的序号有 .
12. 把“两个邻角的角平分线互相垂直”写成“如果那么”的形式为______________________________________________________________________________.
13. 写出命题“如果,那么”的题设:________,结论:________.
14. 如图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为,,,每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小,如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买,号座位的票,乙购买,,号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序______.
三、解答题.
15. 如图,已知,求证:E.
16. 如图,,,求证:.
17. 完成下面的证明.
如图,,求证:.
证明:,
____________;
,
______.
.
如图,,,分别是,的平分线.
求证.
证明:,分别是,的平分线,
,____________
又,
.
______.
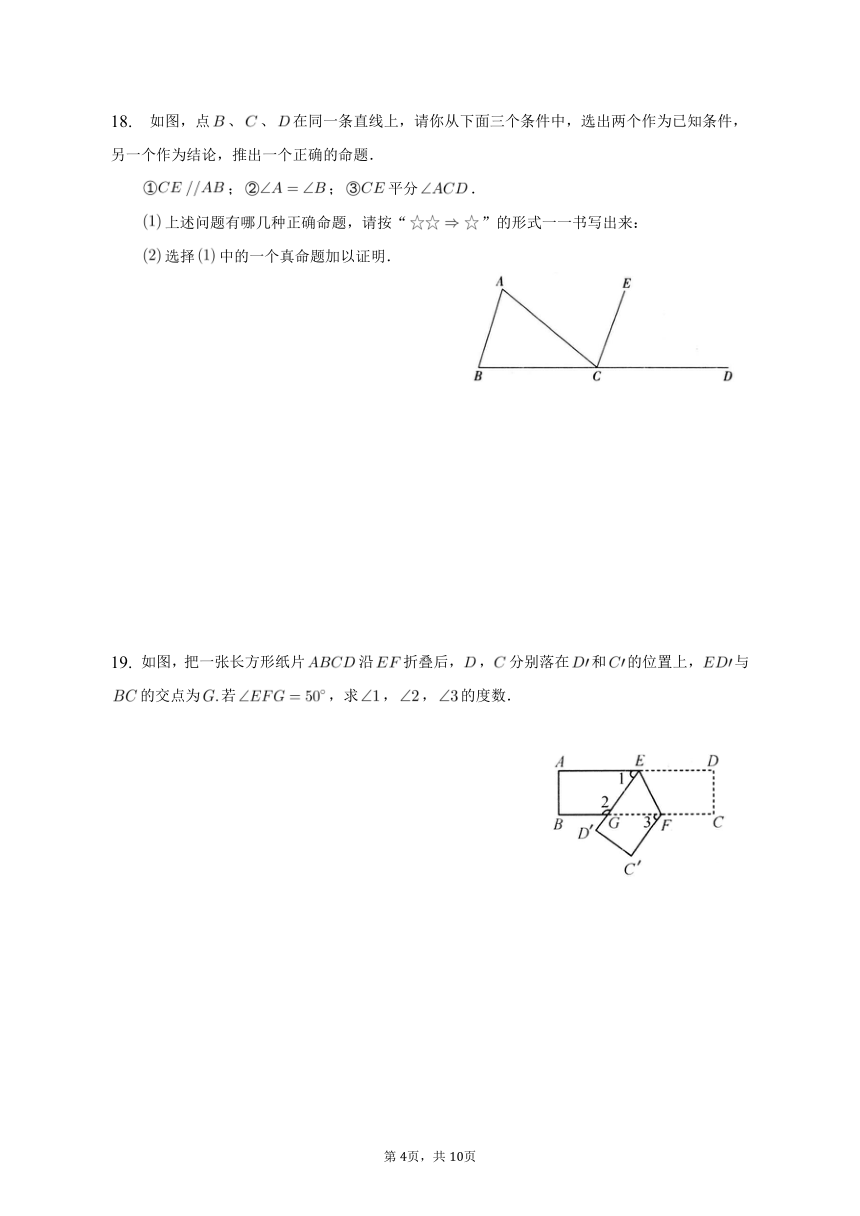
18. 如图,点、、在同一条直线上,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
;;平分.
上述问题有哪几种正确命题,请按“”的形式一一书写出来:
选择中的一个真命题加以证明.
19. 如图,把一张长方形纸片沿折叠后,,分别落在和的位置上,与的交点为若,求,,的度数.
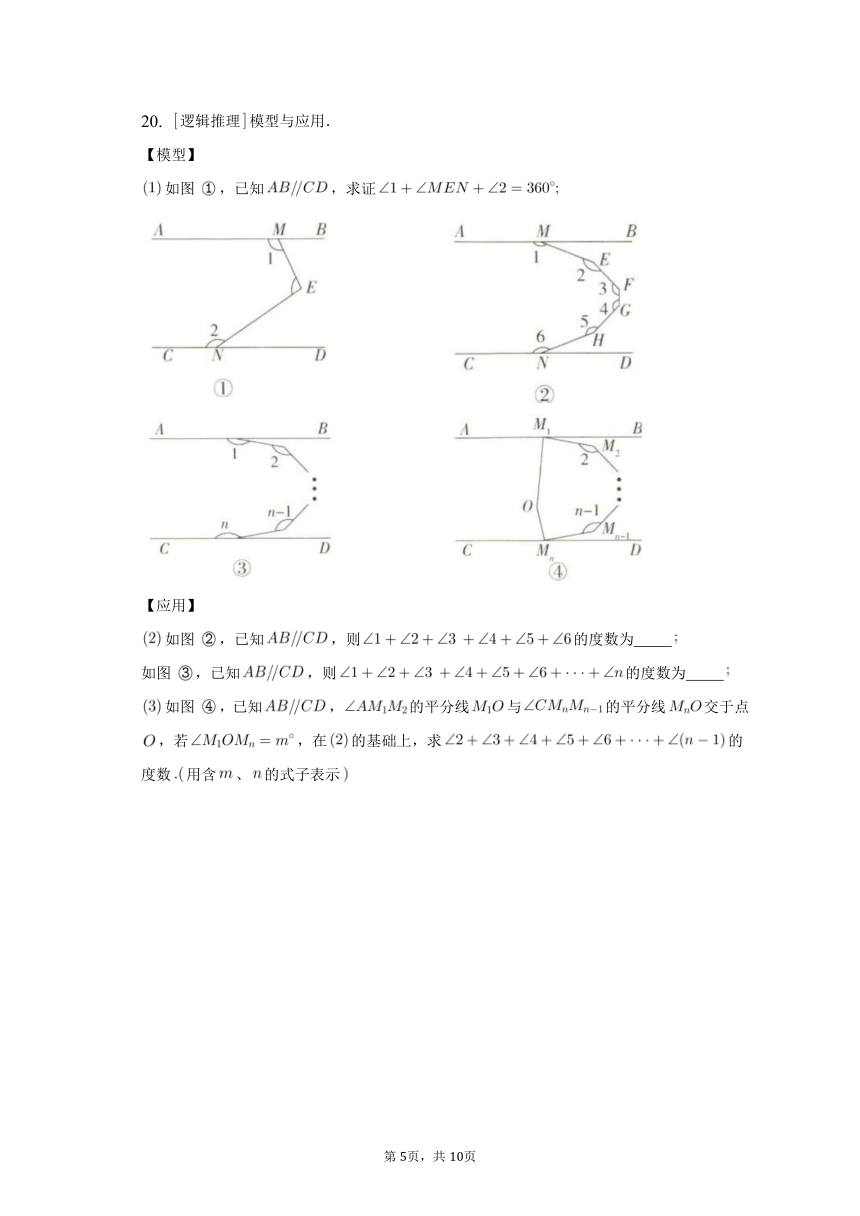
20. 逻辑推理模型与应用.
【模型】
如图,已知,求证
【应用】
如图,已知,则的度数为
如图,已知,则的度数为
如图,已知,的平分线与的平分线交于点,若,在的基础上,求的度数用含、的式子表示
5.3.2 命题、定理、证明 同步练习
参考答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】两个角是对顶角
10.【答案】真
11.【答案】
12.【答案】如果作两个邻补角的角平分线,那么这两条角平分线互相垂直
13.【答案】;
14.【答案】丙、丁、甲、乙答案不唯一.
15.【答案】证明:,
.
,
,
,
E.
16.【答案】证明:如图,作.
,
.
,
.
,,
.
.
,
.
,
,即,
.
17.【答案】解:证明:,
两直线平行,内错角相等;
,
两直线平行,同旁内角互补.
.
证明:,分别是,的平分线,
,角平分线的定义.
又,
.
等量代换.
18.【答案】解:上述问题有三种正确命题,分别是:
命题:;命题:;命题:.
解:选择命题:.
证明:,,.
,.
平分.
选择命题:.
证明:,,.
平分,.
.
选择命题:.
证明:平分,.
,
,
.
,
.
19.【答案】解:如图:
,,
,
由折叠的性质可得,
,
,
,
四边形为长方形,
,
故,,.
20.【答案】解:证明:如图,过点作,则,
,,
过作,过作,过作,过作,
,
,
,, ,,
, ,
同理可得,
故答案为.
如图,过点作,
,
,
,
同理可得,
,
,
平分,
,
同理可得,
,
又,
.
第1页,共1页
同步练习
一、选择题.
1. 下列语句中,是命题的是( )
A. 两个相等的角是对顶角 B. 在直线上任取一点
C. 用量角器量角的度数 D. 直角都相等吗?
2. 下列说法中,正确的是( )
A. “同位角相等”是一个真命题
B. 图形的平移是指把图形沿水平方向移动
C. “凡直角都相等”是一个假命题
D. 在平移的过程中,对应线段互相平行或在同一条直线上且相等
3. 下列命题中,是假命题的是( )
A. 对顶角相等 B. 两直线平行,同旁内角互补
C. 和度的两个角是邻补角 D. 垂线段最短
4. 下列命题中,真命题的个数是( )
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
两条直线被第三条直线所截,同旁内角互补
两直线平行,内错角相等
同一平面内,过一点有且只有一条直线与已知直线垂直
从直线外一点到这条直线的垂线段,叫做这点到直线的距离
A. 个 B. 个 C. 个 D. 个
5. 下列命题中,是真命题的有( )
同位角相等对顶角相等同一平面内,如果直线,直线,那么同一平面内,如果直线,直线,那么.
A. 个 B. 个 C. 个 D. 个
6. 下列语句中,是命题的是( )
若,,则;内错角相等吗?
画线段;如果,,那么;直角都相等
A. B. C. D.
7. 对假命题“任何一个角的补角都不小于这个角”举反例,下列选项中,正确的是( )
A. ,的补角,
B. ,的补角,
C. ,的补角,
D. 互为邻补角的两个角
8. 能说明“锐角,锐角的和是锐角”是假命题的例证图是( )
A. B.
C. D.
二、填空题.
9. 命题“对顶角相等”的题设是 .
10. “对顶角相等”是一个______命题填“真”或“假”.
11. 已知命题:如果,那么;如果,那么;等角的余角相等;两个相等的角是对顶角.其中是假命题的序号有 .
12. 把“两个邻角的角平分线互相垂直”写成“如果那么”的形式为______________________________________________________________________________.
13. 写出命题“如果,那么”的题设:________,结论:________.
14. 如图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为,,,每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小,如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买,号座位的票,乙购买,,号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序______.
三、解答题.
15. 如图,已知,求证:E.
16. 如图,,,求证:.
17. 完成下面的证明.
如图,,求证:.
证明:,
____________;
,
______.
.
如图,,,分别是,的平分线.
求证.
证明:,分别是,的平分线,
,____________
又,
.
______.
18. 如图,点、、在同一条直线上,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
;;平分.
上述问题有哪几种正确命题,请按“”的形式一一书写出来:
选择中的一个真命题加以证明.
19. 如图,把一张长方形纸片沿折叠后,,分别落在和的位置上,与的交点为若,求,,的度数.
20. 逻辑推理模型与应用.
【模型】
如图,已知,求证
【应用】
如图,已知,则的度数为
如图,已知,则的度数为
如图,已知,的平分线与的平分线交于点,若,在的基础上,求的度数用含、的式子表示
5.3.2 命题、定理、证明 同步练习
参考答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】两个角是对顶角
10.【答案】真
11.【答案】
12.【答案】如果作两个邻补角的角平分线,那么这两条角平分线互相垂直
13.【答案】;
14.【答案】丙、丁、甲、乙答案不唯一.
15.【答案】证明:,
.
,
,
,
E.
16.【答案】证明:如图,作.
,
.
,
.
,,
.
.
,
.
,
,即,
.
17.【答案】解:证明:,
两直线平行,内错角相等;
,
两直线平行,同旁内角互补.
.
证明:,分别是,的平分线,
,角平分线的定义.
又,
.
等量代换.
18.【答案】解:上述问题有三种正确命题,分别是:
命题:;命题:;命题:.
解:选择命题:.
证明:,,.
,.
平分.
选择命题:.
证明:,,.
平分,.
.
选择命题:.
证明:平分,.
,
,
.
,
.
19.【答案】解:如图:
,,
,
由折叠的性质可得,
,
,
,
四边形为长方形,
,
故,,.
20.【答案】解:证明:如图,过点作,则,
,,
过作,过作,过作,过作,
,
,
,, ,,
, ,
同理可得,
故答案为.
如图,过点作,
,
,
,
同理可得,
,
,
平分,
,
同理可得,
,
又,
.
第1页,共1页
