高二年级上 数学第六章不等式教学教案-人教版[上学期]
文档属性
| 名称 | 高二年级上 数学第六章不等式教学教案-人教版[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 896.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-14 00:00:00 | ||
图片预览



文档简介
第六章 不等式
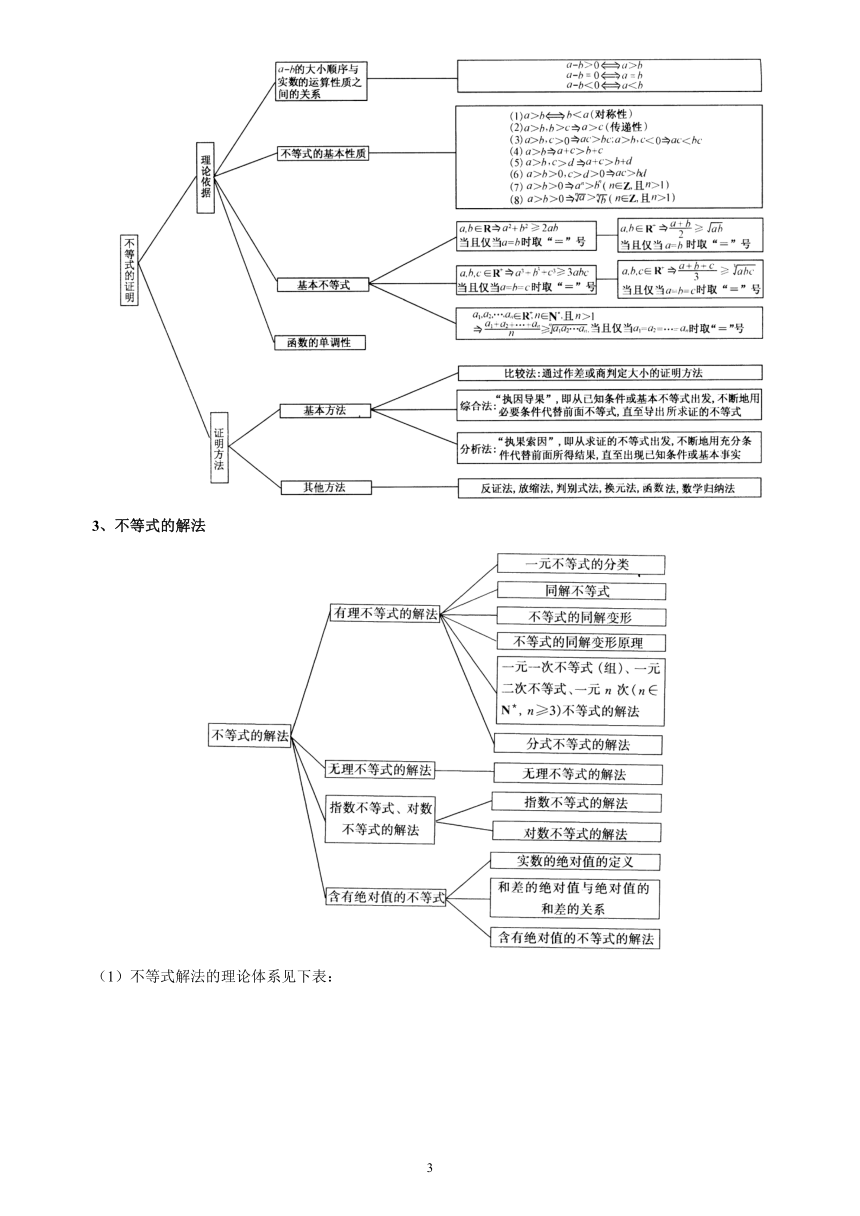
一、知识框架
二、重点难点
重点:实数的大小顺序与实数的运算性质之间的关系,不等式的8条性质;用作差法解答不等式问题;5个基本不等式;不等式的证明方法;各种不等式的解法,不等式的同解变形;
难点: 对不等式8条性质的正确运用;领悟作商法适合的题型;正确运用不等式的性质和5个基本不等式证明简单的不等式;证明方法所适用的题型;解各种不等式;分类讨论“标准”的确定;用分类讨论思想解不等式;
三、知识点解析
1、不等式的性质
(1)的大小顺序(实数的顺序性)与实数的运算性质之间的关系:
1)设,则①;②;③;
2)设,则①;②;③;
(2)不等式的概念:
1)不等式的定义:用不等号()表示不等关系的式子叫做不等式,分为严格不等式和非严格不等式;
2)同向、异向不等式:与叫做同向不等式,与叫做异向不等式;
3)不等式的解集:使成立的的集合,叫做的解集;
4)同解不等式:若与(或)的解集相等,则与(或)叫做同解不等式;
5)不等式的同解变形:一个不等式变形为与它同解的不等式,这样的变形成为不等式的同解变形;
6)证明不等式;
7)解不等式;
(3)不等式的基本性质:①(对称性);②(传递性);③(可加性);④;⑤(可乘性);⑥;⑦;⑧;
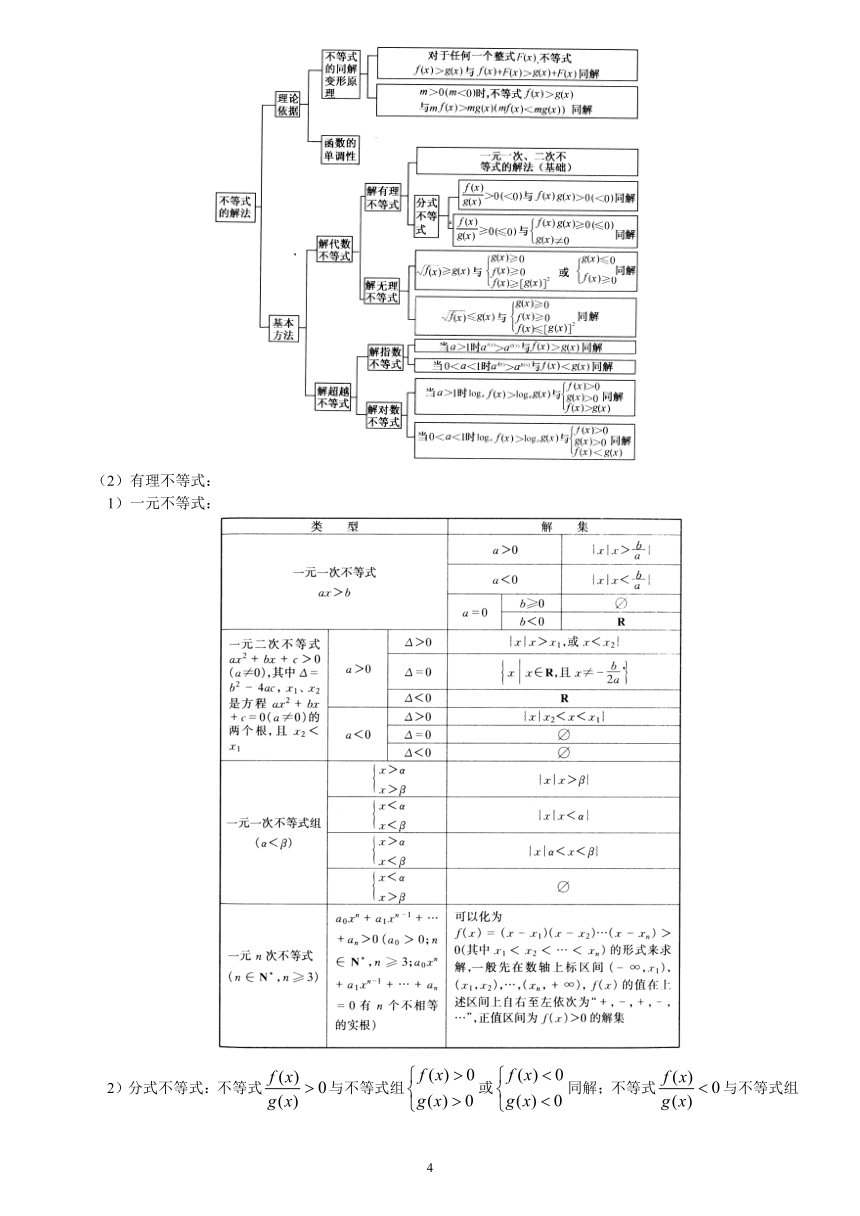
2、不等式的证明
1)算术平均数与集合平均数:几个基本不等式(见下表);
2)不等式的证明:下表是不等式证明的理论体系:
3、不等式的解法
(1)不等式解法的理论体系见下表:
(2)有理不等式:
1)一元不等式:
2)分式不等式:不等式与不等式组或同解;不等式与不等式组或同解。
(3)无理不等式:与或同解;与同解;与同解;
(4)指数不等式:时,与同解;时,与同解;
(5)对数不等式:时,与同解;时,与同解;
(6)含绝对值得不等式:,,;
4、不等式的应用
四、例题
1、不等式的性质
例1 比较与的大小。
分析 作差比较。
解 ,
。
例2 已知,比较与的大小。
分析 作差比较。
解 ,由,得,从而。
思考 当去掉条件时,则大小关系如何?
例3 设,且,比较与的大小。
分析 作差比较。
解 ,
当时,,,则,;
当时,,,则,。
总结 比较两个实数(代数式)大小的思维过程是:作差→变形→判断符号→结论。
例4 判断下列各命题的真假,说明理由:(1)如果,那么;(2)如果,那么;(3)如果,那么。
分析 判断一个命题的真假的方法是:如果判定是真命题,则必须给出它的证明;如果判定是假命题,只要举出一个反例即可。
解 根据不等式的性质可判定如下:真命题是(1)、(3).假命题是(2)。
例5 回答下列问题:
(1)如果,,能否断定与谁大谁小?举例说明;
(2)如果,,能否断定与谁大谁小?举例说明.
分析 解答本题的方法是:如果作肯定回答,则必须给出它的证明;如果作否定回答,则必须举出反例。
解 (1)不能断定;(2)不能断定.举例略.
注意 本例举例要举出3个例子,使得两代数式的值能体现出大于、小于、相等三种情况.
例7 已知,,求证。
解 由知,则知,,。
2、不等式的证明
例1 已知是正数,且,求证。
证明 ,。
说明 本题条件下可证明。
例2 甲乙两人同时同地沿同一路线走到同一地点,甲有一半时间以速度m行走,另一半时间以速度n行走;有一半路程乙以速度m行走,另一半路程以速度n行走,如果m n,问:甲乙两人谁先到达指定地点?
解 设从出发地到指定地点的路程为S,甲乙两人走完全程所需时间分别是t1, t2,
则: 可得:
∴
∵S, m, n都是正数,且m n, ∴t1 t2 < 0 即:t1 < t2,从而,甲先到到达指定地点。
例3 设a, b R+,求证:
证明 作商:
当a = b时,;
当a > b > 0时,;
当b > a > 0时, 。
∴ 。
同理可证。
例4 求证
证明 因为都是正数,所以为了证明,只需证明,展开得 ,即 。因为成立,所以 成立,即证明了。
例5 证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大.
分析 当水的流速相同时,水管的流量取决于水管截面面积的大小,设截面的周长为L,则周长为L的圆的半径为,截面积为;周长为L的正方形边长为,截面积为.所以本题只需证明。
说明 对于较复杂的不等式,直接运用综合法往往不易入手,因此,通常用分析法探索证题途径,然后用综合法加以证明,所以分析法和综合法经常是结合在一起使用的。
例6 已知x > 0 , y > 0,2x + y = 1,求证:
证一 即:;
证二 由x > 0 , y > 0,2x + y = 1,可设,
则。
例7 若,求证:
证 设,
则
小结 若0≤x≤1,则可令x = sin ()或x = sin2 ()。
若,则可令x = cos , y = sin ()。
若,则可令x = sec, y = tan ()。
若x≥1,则可令x = sec ()。
若xR,则可令x = tan ()。
例8 证明:在是增函数。
证 设2≤x1∵x2 x1 > 0, x1 + x2 4 > 0 ∴。
又∵y1 > 0, ∴y1 > y2 ∴在是增函数。
例9 设a, b, c R,
1 求证:,
2 求证:
证 1 ∵ ∴ ∴
2 同理:,
三式相加:
例10 a , b, cR+, 求证:1 ,2 ,3 。
证 1 法一:, , 两式相乘即得。
法二:左边≥ 3 + 2 + 2 + 2 = 9。
2 ∵,
,两式相乘即得。
3 由上题:, ∴,
即:
3、不等式的解法
例1 解关于x的不等式
解 将原不等式展开,整理得:
讨论 当时,;
当时,若≥0时;若<0时;
当时,。
例2 解关于x的不等式
解 原不等式可以化为:。
若即则或;
若即则,;
若即则或。
例3 关于x的不等式的解集为,求关于x的不等式的解集。
解 由题设且, ,从而 可以变形为,即: ∴。
例4 关于x的不等式 对于恒成立,求a的取值范围.
解:当时不合,也不合,
∴必有: 。
例5 若函数的定义域为R,求实数k的取值范围。
解 显然k=0时满足 而k<0时不满足,∴k的取值范围是[0,1]。
例6 解不等式
略解一(分析法),
或,。
解二 (列表法)原不等式可化为列表
注意 按根的由小到大排列
解三 (标根法)作数轴;标根;画曲线,定解
小结:在某一区间内,一个式子是大于0(还是小于0)取决于这个式子的各因式在此区间内的符号;而区间的分界线就是各因式的根;上述的列表法和标根法,几乎可以使用在所有的有理分式与高次不等式,其中最值得推荐的是“标根法”
例7 解不等式
解 原不等式化为 , ∴原不等式的解为。
例8 解不等式
解 ∵恒成立,∴原不等式等价于 即。
例9 解不等式
解 原不等式等价于且 ,∴原不等式的解为。
例10 解不等式
解 原不等式等价于
即:,,
,
∴。
例11 解不等式
解 原不等式等价于,∴原不等式的解为:。
例12 k为何值时,下式恒成立:
解 原不等式可化为:,而,
∴原不等式等价于,由得1例13 解不等式
解 ∵根式有意义 ∴必须有:
又有 ∵ 原不等式可化为,两边平方得:,解之:。
∴。
例14 解不等式
解 原不等式等价于下列两个不等式组得解集的并集:
Ⅰ: Ⅱ:
解Ⅰ: 解Ⅱ:。
∴原不等式的解集为。
例15 解不等式
解 原不等式等价于。
例16 解不等式
解 要使不等式有意义必须:,
原不等式可变形为 ,因为两边均为非负。∴ 即。∵x+1≥0,∴不等式的解为2x+1≥0,即 。
例17 解不等式
解 要使不等式有意义必须:,因为不等式两边均为非负,两边平方得:,即>x。因为两边非负,再次平方:,解之0综合 得:原不等式的解集为0例18 解不等式
解 定义域 x-1≥0,x≥1,原不等式可化为:,两边立方并整理得:,在此条件下两边再平方, 整理得:。解之并联系定义域得原不等式的解为。
例19 解不等式
解 原不等式可化为:,∵底数,∴,整理得:,解之,不等式的解集为。
例20 解不等式
解 原不等式可化为:,即:,解之: 或,∴x>2或,∴不等式的解集为。
例21 解不等式
解 原不等式等价于 或,解之得:,∴原不等式的解集为。
4、不等式的应用
例1 证明下列各题:
⑴
证 ∵ ∴,,于是。
⑵若上题改成,结果将如何?
解 ∵ ,于是,从而。
⑶若 则
解:若则显然有;若异号或一个为0则;∴。
例2.若,则为何值时有最小值,最小值为几?
解 ∵ ∴ ,
∴=,当且仅当即时。
例3 求函数的最大值,下列解法是否正确?为什么?
解 ,当且仅当即时。
例4 若,求的最值
解:,
∵,∴,。
从而 ,即。
例5 设且,求的最大值
解 ∵ ∴
又,∴,即。
例6 已知且,求的最小值
解 ,
当且仅当即时。
例7 将一块边长为的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
解 设剪去的小正方形的边长为,则其容积为,
,
当且仅当即时取“=”,即当剪去的小正方形的边长为时,铁盒的容积为。
-1
0
1
2
3
4
-2
PAGE
1
一、知识框架
二、重点难点
重点:实数的大小顺序与实数的运算性质之间的关系,不等式的8条性质;用作差法解答不等式问题;5个基本不等式;不等式的证明方法;各种不等式的解法,不等式的同解变形;
难点: 对不等式8条性质的正确运用;领悟作商法适合的题型;正确运用不等式的性质和5个基本不等式证明简单的不等式;证明方法所适用的题型;解各种不等式;分类讨论“标准”的确定;用分类讨论思想解不等式;
三、知识点解析
1、不等式的性质
(1)的大小顺序(实数的顺序性)与实数的运算性质之间的关系:
1)设,则①;②;③;
2)设,则①;②;③;
(2)不等式的概念:
1)不等式的定义:用不等号()表示不等关系的式子叫做不等式,分为严格不等式和非严格不等式;
2)同向、异向不等式:与叫做同向不等式,与叫做异向不等式;
3)不等式的解集:使成立的的集合,叫做的解集;
4)同解不等式:若与(或)的解集相等,则与(或)叫做同解不等式;
5)不等式的同解变形:一个不等式变形为与它同解的不等式,这样的变形成为不等式的同解变形;
6)证明不等式;
7)解不等式;
(3)不等式的基本性质:①(对称性);②(传递性);③(可加性);④;⑤(可乘性);⑥;⑦;⑧;
2、不等式的证明
1)算术平均数与集合平均数:几个基本不等式(见下表);
2)不等式的证明:下表是不等式证明的理论体系:
3、不等式的解法
(1)不等式解法的理论体系见下表:
(2)有理不等式:
1)一元不等式:
2)分式不等式:不等式与不等式组或同解;不等式与不等式组或同解。
(3)无理不等式:与或同解;与同解;与同解;
(4)指数不等式:时,与同解;时,与同解;
(5)对数不等式:时,与同解;时,与同解;
(6)含绝对值得不等式:,,;
4、不等式的应用
四、例题
1、不等式的性质
例1 比较与的大小。
分析 作差比较。
解 ,
。
例2 已知,比较与的大小。
分析 作差比较。
解 ,由,得,从而。
思考 当去掉条件时,则大小关系如何?
例3 设,且,比较与的大小。
分析 作差比较。
解 ,
当时,,,则,;
当时,,,则,。
总结 比较两个实数(代数式)大小的思维过程是:作差→变形→判断符号→结论。
例4 判断下列各命题的真假,说明理由:(1)如果,那么;(2)如果,那么;(3)如果,那么。
分析 判断一个命题的真假的方法是:如果判定是真命题,则必须给出它的证明;如果判定是假命题,只要举出一个反例即可。
解 根据不等式的性质可判定如下:真命题是(1)、(3).假命题是(2)。
例5 回答下列问题:
(1)如果,,能否断定与谁大谁小?举例说明;
(2)如果,,能否断定与谁大谁小?举例说明.
分析 解答本题的方法是:如果作肯定回答,则必须给出它的证明;如果作否定回答,则必须举出反例。
解 (1)不能断定;(2)不能断定.举例略.
注意 本例举例要举出3个例子,使得两代数式的值能体现出大于、小于、相等三种情况.
例7 已知,,求证。
解 由知,则知,,。
2、不等式的证明
例1 已知是正数,且,求证。
证明 ,。
说明 本题条件下可证明。
例2 甲乙两人同时同地沿同一路线走到同一地点,甲有一半时间以速度m行走,另一半时间以速度n行走;有一半路程乙以速度m行走,另一半路程以速度n行走,如果m n,问:甲乙两人谁先到达指定地点?
解 设从出发地到指定地点的路程为S,甲乙两人走完全程所需时间分别是t1, t2,
则: 可得:
∴
∵S, m, n都是正数,且m n, ∴t1 t2 < 0 即:t1 < t2,从而,甲先到到达指定地点。
例3 设a, b R+,求证:
证明 作商:
当a = b时,;
当a > b > 0时,;
当b > a > 0时, 。
∴ 。
同理可证。
例4 求证
证明 因为都是正数,所以为了证明,只需证明,展开得 ,即 。因为成立,所以 成立,即证明了。
例5 证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大.
分析 当水的流速相同时,水管的流量取决于水管截面面积的大小,设截面的周长为L,则周长为L的圆的半径为,截面积为;周长为L的正方形边长为,截面积为.所以本题只需证明。
说明 对于较复杂的不等式,直接运用综合法往往不易入手,因此,通常用分析法探索证题途径,然后用综合法加以证明,所以分析法和综合法经常是结合在一起使用的。
例6 已知x > 0 , y > 0,2x + y = 1,求证:
证一 即:;
证二 由x > 0 , y > 0,2x + y = 1,可设,
则。
例7 若,求证:
证 设,
则
小结 若0≤x≤1,则可令x = sin ()或x = sin2 ()。
若,则可令x = cos , y = sin ()。
若,则可令x = sec, y = tan ()。
若x≥1,则可令x = sec ()。
若xR,则可令x = tan ()。
例8 证明:在是增函数。
证 设2≤x1
又∵y1 > 0, ∴y1 > y2 ∴在是增函数。
例9 设a, b, c R,
1 求证:,
2 求证:
证 1 ∵ ∴ ∴
2 同理:,
三式相加:
例10 a , b, cR+, 求证:1 ,2 ,3 。
证 1 法一:, , 两式相乘即得。
法二:左边≥ 3 + 2 + 2 + 2 = 9。
2 ∵,
,两式相乘即得。
3 由上题:, ∴,
即:
3、不等式的解法
例1 解关于x的不等式
解 将原不等式展开,整理得:
讨论 当时,;
当时,若≥0时;若<0时;
当时,。
例2 解关于x的不等式
解 原不等式可以化为:。
若即则或;
若即则,;
若即则或。
例3 关于x的不等式的解集为,求关于x的不等式的解集。
解 由题设且, ,从而 可以变形为,即: ∴。
例4 关于x的不等式 对于恒成立,求a的取值范围.
解:当时不合,也不合,
∴必有: 。
例5 若函数的定义域为R,求实数k的取值范围。
解 显然k=0时满足 而k<0时不满足,∴k的取值范围是[0,1]。
例6 解不等式
略解一(分析法),
或,。
解二 (列表法)原不等式可化为列表
注意 按根的由小到大排列
解三 (标根法)作数轴;标根;画曲线,定解
小结:在某一区间内,一个式子是大于0(还是小于0)取决于这个式子的各因式在此区间内的符号;而区间的分界线就是各因式的根;上述的列表法和标根法,几乎可以使用在所有的有理分式与高次不等式,其中最值得推荐的是“标根法”
例7 解不等式
解 原不等式化为 , ∴原不等式的解为。
例8 解不等式
解 ∵恒成立,∴原不等式等价于 即。
例9 解不等式
解 原不等式等价于且 ,∴原不等式的解为。
例10 解不等式
解 原不等式等价于
即:,,
,
∴。
例11 解不等式
解 原不等式等价于,∴原不等式的解为:。
例12 k为何值时,下式恒成立:
解 原不等式可化为:,而,
∴原不等式等价于,由得1
解 ∵根式有意义 ∴必须有:
又有 ∵ 原不等式可化为,两边平方得:,解之:。
∴。
例14 解不等式
解 原不等式等价于下列两个不等式组得解集的并集:
Ⅰ: Ⅱ:
解Ⅰ: 解Ⅱ:。
∴原不等式的解集为。
例15 解不等式
解 原不等式等价于。
例16 解不等式
解 要使不等式有意义必须:,
原不等式可变形为 ,因为两边均为非负。∴ 即。∵x+1≥0,∴不等式的解为2x+1≥0,即 。
例17 解不等式
解 要使不等式有意义必须:,因为不等式两边均为非负,两边平方得:,即>x。因为两边非负,再次平方:,解之0
解 定义域 x-1≥0,x≥1,原不等式可化为:,两边立方并整理得:,在此条件下两边再平方, 整理得:。解之并联系定义域得原不等式的解为。
例19 解不等式
解 原不等式可化为:,∵底数,∴,整理得:,解之,不等式的解集为。
例20 解不等式
解 原不等式可化为:,即:,解之: 或,∴x>2或,∴不等式的解集为。
例21 解不等式
解 原不等式等价于 或,解之得:,∴原不等式的解集为。
4、不等式的应用
例1 证明下列各题:
⑴
证 ∵ ∴,,于是。
⑵若上题改成,结果将如何?
解 ∵ ,于是,从而。
⑶若 则
解:若则显然有;若异号或一个为0则;∴。
例2.若,则为何值时有最小值,最小值为几?
解 ∵ ∴ ,
∴=,当且仅当即时。
例3 求函数的最大值,下列解法是否正确?为什么?
解 ,当且仅当即时。
例4 若,求的最值
解:,
∵,∴,。
从而 ,即。
例5 设且,求的最大值
解 ∵ ∴
又,∴,即。
例6 已知且,求的最小值
解 ,
当且仅当即时。
例7 将一块边长为的正方形铁皮,剪去四个角(四个全等的正方形),作成一个无盖的铁盒,要使其容积最大,剪去的小正方形的边长为多少?最大容积是多少?
解 设剪去的小正方形的边长为,则其容积为,
,
当且仅当即时取“=”,即当剪去的小正方形的边长为时,铁盒的容积为。
-1
0
1
2
3
4
-2
PAGE
1
