不等式高考复习[上学期]
图片预览






文档简介
课件21张PPT。1第六章 不等式高考复习 不 等 式
高考要点综述2006年11月15日2考点要求:(1)了解不等式的有关概念和及其分类;掌握不等式的性质及其运用;明确各个性质成立的前提条件;理解绝对值不等式的概念与性质; (2)掌握两个正数的算术平均数不于它们的几何平均数的定理,并会简单的应用. (3)掌握用比较法、分析法和综合法证明简单的不等式. (4)熟练掌握一元一次不等式(组),一元二次不等式组的解法.在此基础上,掌握一些简单的高次整式不等式和分式不等式及绝对值不等式的解法;掌握含字母类高次整式不等式和分式不等式的解法;
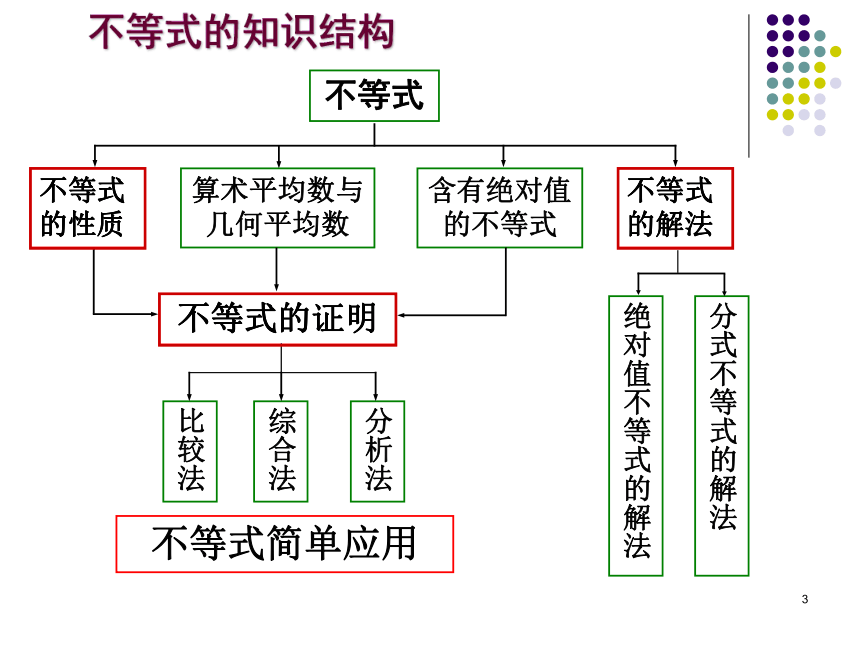
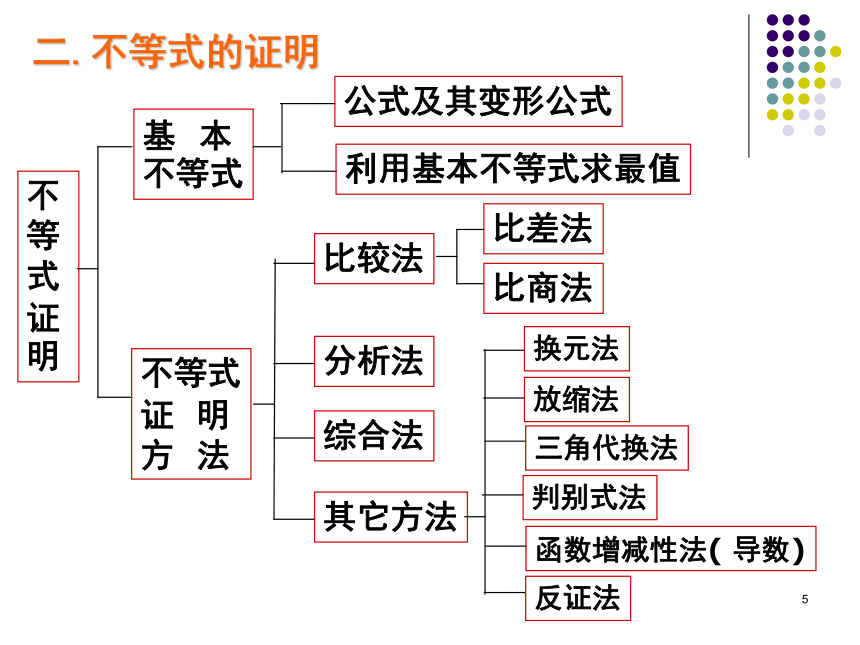
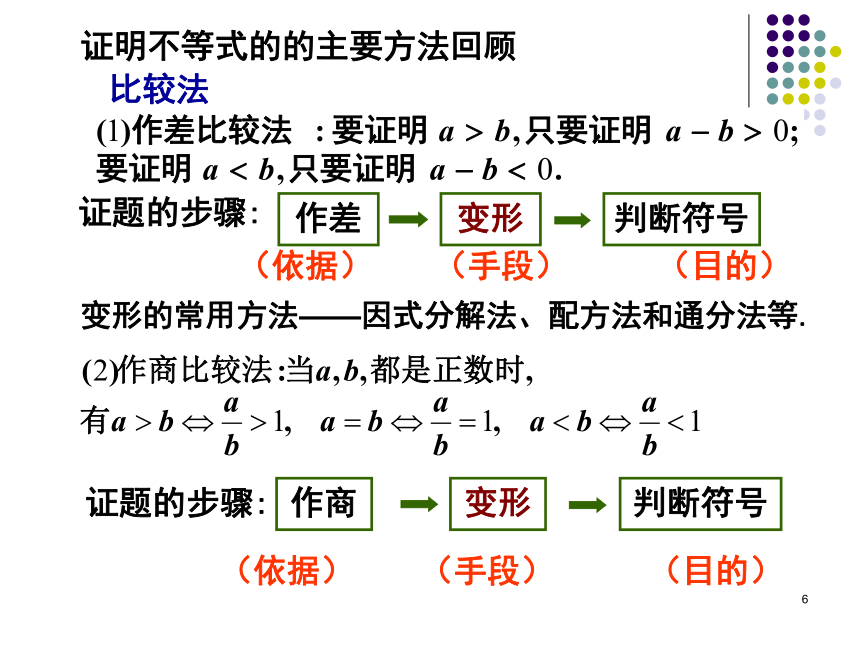
(5)灵活运用不等式的性质求函数的定义域、值域和最值;熟练掌握运用不等式解决实际问题。3不等式的知识结构不等式不等式简单应用不等式的性质不等式的解法不等式的证明4一.不等式的性质1.不等式的最基本性质2.不等式的主要性质5二.不等式的证明6证明不等式的的主要方法回顾变形的常用方法——因式分解法、配方法和通分法等.比较法7综合法——利用某些已知证明过的不等式(例如算术平均数与几何平均数的定理)和不等式的性质推导出所要证明的不等式成立.分析法——证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题.如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立.思维特点是“由因导果”.即由已知条件出发,利用已知的数学定理、性质和公式,推导结论的一种证明方法.思维特点是“执果索因”,即从结论开始,一步步寻上一步成立的充分条件,直至得出一个真命题为止.它与综合法的证明过程恰恰相反.8一、不等式性质运用
1、比较大小问题;
2、根据不等式性质判断有关不等式命题的真假;
3、运用不等式性质确定代数式的范围;
4、运用不等式性质处理不等式与函数的综合问题。5. 重点例题93 、 已知 且
求 的取值范围。解:错误原因:多次
运用不等式性质
容易放大范围。运用:“线性表示
法”准确求范围1011练习:已知:
求 的范围。解:《三尺》P159
例3 、练习3121314二、算术平均数与几何平均数1、定理及推论2、均值定理 应用均值定理求最值要特别注意:两个变元都为正值;两个变元之积(或和)为定值;当且仅当x=y时等号成立;这三个条件缺一不可,即编成口诀:“一正,二定,三相等”同时成立.153、题型(1)利用均值不等式求最值;
(2)利用均值不等式求取值范围;
(3)利用均值不等式证明不等式;
(4)利用均值不等式解决实际问题;
(5)均值不等式与函数单调性的综合运用。4、解题注意事项(1) “一正、二定、三相等”;
(2) 利用均值不等式解决与其它单元知识的综合题
时,列出函数关系式或方程后通过恒等变形构造出
运用均值不等式的的形式是关键。16说明:“一正”、“三相等”这两个条件容易获得;“二
定”条件的获得往往是一个难点。解决它需要一定的
分拆、凑配的技巧。1718多次运用均值不等式,要注意取等号条件的一致性。
如果等号成立的条件不一致,则此时最小值取不到。1920练习:某工厂拟建一座平面图为矩形且面积为200m2的三级污水处理池.如果池四周围墙建造单价为400元/m,中间两道隔墙建造单价为248元/m,池底建造80元/m2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求最低造价. 2.对于应用题要认真阅读理解题意,从中提炼出与解题有关的信息,建立数学摸型.本题计算量较大,要仔细、认真,避免计算出错. 评注:1.用“平均值定理”求函数最值时应注意的问题.对原题增加限制条件:“水池的长和宽都不得超过16m”,就不能照搬上述解法了.为什么?21
高考要点综述2006年11月15日2考点要求:(1)了解不等式的有关概念和及其分类;掌握不等式的性质及其运用;明确各个性质成立的前提条件;理解绝对值不等式的概念与性质; (2)掌握两个正数的算术平均数不于它们的几何平均数的定理,并会简单的应用. (3)掌握用比较法、分析法和综合法证明简单的不等式. (4)熟练掌握一元一次不等式(组),一元二次不等式组的解法.在此基础上,掌握一些简单的高次整式不等式和分式不等式及绝对值不等式的解法;掌握含字母类高次整式不等式和分式不等式的解法;
(5)灵活运用不等式的性质求函数的定义域、值域和最值;熟练掌握运用不等式解决实际问题。3不等式的知识结构不等式不等式简单应用不等式的性质不等式的解法不等式的证明4一.不等式的性质1.不等式的最基本性质2.不等式的主要性质5二.不等式的证明6证明不等式的的主要方法回顾变形的常用方法——因式分解法、配方法和通分法等.比较法7综合法——利用某些已知证明过的不等式(例如算术平均数与几何平均数的定理)和不等式的性质推导出所要证明的不等式成立.分析法——证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题.如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立.思维特点是“由因导果”.即由已知条件出发,利用已知的数学定理、性质和公式,推导结论的一种证明方法.思维特点是“执果索因”,即从结论开始,一步步寻上一步成立的充分条件,直至得出一个真命题为止.它与综合法的证明过程恰恰相反.8一、不等式性质运用
1、比较大小问题;
2、根据不等式性质判断有关不等式命题的真假;
3、运用不等式性质确定代数式的范围;
4、运用不等式性质处理不等式与函数的综合问题。5. 重点例题93 、 已知 且
求 的取值范围。解:错误原因:多次
运用不等式性质
容易放大范围。运用:“线性表示
法”准确求范围1011练习:已知:
求 的范围。解:《三尺》P159
例3 、练习3121314二、算术平均数与几何平均数1、定理及推论2、均值定理 应用均值定理求最值要特别注意:两个变元都为正值;两个变元之积(或和)为定值;当且仅当x=y时等号成立;这三个条件缺一不可,即编成口诀:“一正,二定,三相等”同时成立.153、题型(1)利用均值不等式求最值;
(2)利用均值不等式求取值范围;
(3)利用均值不等式证明不等式;
(4)利用均值不等式解决实际问题;
(5)均值不等式与函数单调性的综合运用。4、解题注意事项(1) “一正、二定、三相等”;
(2) 利用均值不等式解决与其它单元知识的综合题
时,列出函数关系式或方程后通过恒等变形构造出
运用均值不等式的的形式是关键。16说明:“一正”、“三相等”这两个条件容易获得;“二
定”条件的获得往往是一个难点。解决它需要一定的
分拆、凑配的技巧。1718多次运用均值不等式,要注意取等号条件的一致性。
如果等号成立的条件不一致,则此时最小值取不到。1920练习:某工厂拟建一座平面图为矩形且面积为200m2的三级污水处理池.如果池四周围墙建造单价为400元/m,中间两道隔墙建造单价为248元/m,池底建造80元/m2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求最低造价. 2.对于应用题要认真阅读理解题意,从中提炼出与解题有关的信息,建立数学摸型.本题计算量较大,要仔细、认真,避免计算出错. 评注:1.用“平均值定理”求函数最值时应注意的问题.对原题增加限制条件:“水池的长和宽都不得超过16m”,就不能照搬上述解法了.为什么?21
