2022-2023学年华东师大版九年级数学下册 二次函数 课后综合练习(无答案)
文档属性
| 名称 | 2022-2023学年华东师大版九年级数学下册 二次函数 课后综合练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.9KB | ||
| 资源类型 | 教案 | ||
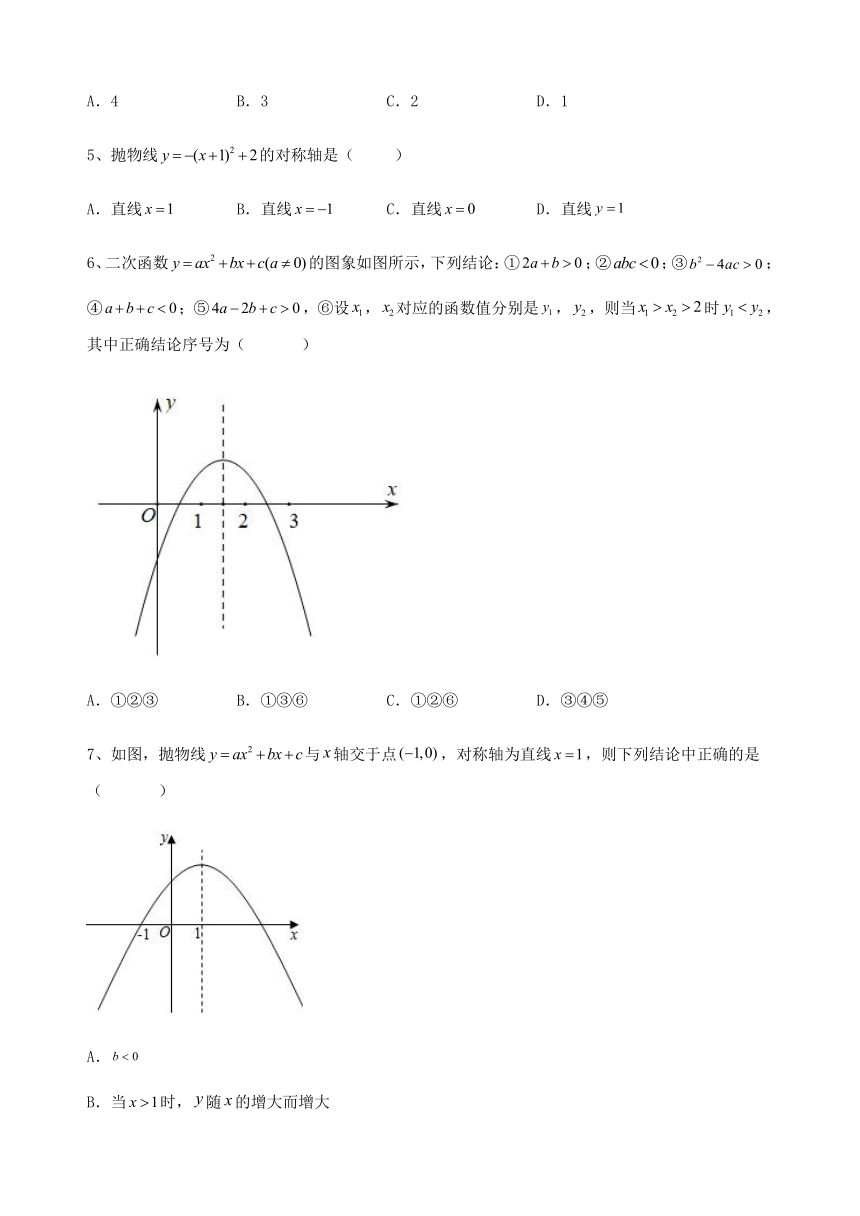
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 19:09:45 | ||
图片预览




文档简介
二次函数课后综合练习
一、单选题(共 10 小题)
1、对于二次函数y=﹣x2+2x+3,下列说法不正确的是( )
A.开口向下
B.当x≥1时,y随x的增大而减小
C.当x=1时,y有最大值3
D.函数图象与x轴交于点(﹣1,0)和(3,0)
2、小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
3、二次函数y=(x+2)2+5的对称轴是( )
A.直线x= B.直线x=5 C.直线x=2 D.直线x=﹣2
4、二次函数y=ax2+bx+c(a≠0)的图象如图所示,与x轴交于点( 1,0)和(x,0),且10;④a+bA.4 B.3 C.2 D.1
5、抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
6、二次函数的图象如图所示,下列结论:①;②;③;④;⑤,⑥设,对应的函数值分别是,,则当时,其中正确结论序号为( )
A.①②③ B.①③⑥ C.①②⑥ D.③④⑤
7、如图,抛物线与轴交于点,对称轴为直线,则下列结论中正确的是( )
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
8、若二次函数与轴的一个交点为,则代数式的值为( )
A. B. C. D.
9、二次函数的自变量与函数值的部分对应值如下表:
… -3 -2 -1 0 1 …
… -11 -3 1 1 -3 …
对于下列结论:①二次函数的图像开口向下;②当时,随的增大而减小;③二次函数的最大值是1;④若,是二次函数图像与轴交点的横坐标,则,其中,正确的是( )
A.①② B.③④ C.①③ D.①②④
10、已知二次函数的图象如图所示,对称轴为直线,下列结论中正确的是( )
A. B. C. D.
二、填空题(共 8 小题)
1、二次函数的图像如图所示,对称轴为直线,根据图中信息可求得该二次函数的解析式为______.
2、已知A(,),B(1,),C(4,)三点都在二次函数的图象上,则、、的大小关系为_______.
3、已知函数,当x______时,y随x的增大而减少.
4、一名男生推铅球,铅球行进的高度y(单位:米)与水平距离x(单位:米)之间的关系为,则这名男生这次推铅球的成绩是______米.
5、在东京奥运会跳水比赛中,中国小花全红婵的表现,令人印象深刻.在正常情况下,跳水运动员进行10米跳台训练时,必须在距水面5米之前完成规定的翻腾动作,并调整好入水姿势,否则容易出现失误.假设某运动员起跳后第t秒离水面的高度为h米,且.那么为了避免出现失误,这名运动员最多有_____秒时间,完成规定的翻腾动作.
6、在平面直角坐标系中,已知点,点,如果二次函数的图象与线段有交点,那么a的取值范围为__________.
7、二次函数y=ax2+bx+4的图象如图所示,则关于x的方程a(x+1)2+b(x+1)=﹣4的根为______.
8、某地的药材批发公司指导农民养植和销售某种药材,经市场调研发现1-8月份这种药材售价(元)与月份之间存在如下表所示的一次函数关系,同时,每千克的成本价(元)与月份之间近似满足如图所示的抛物线,观察两幅图表,试判断_____ 月份出售这种药材获利最大.
月份 ... 3 6 ...
每千克售价 ... 8 6 ...
三、解答题(共 6 小题)
1、如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),点P为抛物线上的一动点.
(1)求二次函数的解析式;
(2)如图,过点A作AC平行于x轴,交抛物线于点C,若点P在AC的上方,作PD平行于y轴交AB于点D,连接PA,PC,当S四边形APCD=时,求点P坐标;
(3)设抛物线的对称轴与AB交于点M,点Q在直线AB上,当以点M、E、P、Q为顶点的四边形为平行四边形时,请直接写出点Q的坐标.
2、如图,抛物线y=﹣x2+bx+c与x轴交于点B(1,0)点,与y轴交于点C(0,3),对称轴l与x轴交于点F,点E是直线AC上方抛物线上一动点,连接AE、EC.
(1)求抛物线的解析式;
(2)当四边形AECO面积最大时,求点E的坐标;
(3)在(2)的条件下,连接EF,点P是x轴上一动点,在抛物线上是否存在点Q,使得以F、E、P、Q为顶点的四边形是平行四边形.若存在,请直接写出点Q的坐标;若不存在,说明理由.
3、如图1,在平面直角坐标系中,抛物线与轴交于点和点,与轴交于点,经过点的直线与抛物线交于另一点,点为抛物线的顶点,抛物线的对称轴与轴交于点.
(1)求直线的解析式;
(2)如图2,点为直线上方抛物线上一动点,直线与轴交于点,连接,.当四边形的面积最大时,求点的坐标以及四边形面积的最大值.
(3)如图3,连接,将(1)中抛物线沿射线平移得到新抛物线,经过点,的顶点为点.在新抛物线上是否存在点,使得是以为直角边的直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
4、如图,抛物线y= x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,3),点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求抛物线的解析式,并写出此抛物线的对称轴和顶点坐标;
(2)如果以点P、N、B、O为顶点的四边形为平行四边形,求m的值;
(3)如果以B、P、N为顶点的三角形与△ABO相似,求点M的坐标.
5、实验表明,汽车急刹车的停车距离等于反应距离与制动距离之和;反应距离与汽车速度成正比,制动距离与汽车速度的平方成正比.已知当汽车的速度为时,急刹车的停车距离为;当汽车的速度为时,急刹车的停车距离为.设汽车的速度为,急刹车的停车距离为.
(1)求关于的函数表达式;
(2)一辆汽车以的速度行驶,突然发现正前方处有一障碍物,紧急刹车,问汽车与障碍物是否会相撞?并说明理由;
(3)一辆行驶中的汽车突然发现正前方处有一辆抛锚的危险用品运输车,紧急刹车,要使汽车距离运输车不小于处停住,则汽车行驶的最大速度是__________.
6、如图,在平面直角坐标系中,已知抛物线经过点A(2,0)和点,顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与轴交于点P,如果点C在轴上,且与相似,求点C的坐标.
一、单选题(共 10 小题)
1、对于二次函数y=﹣x2+2x+3,下列说法不正确的是( )
A.开口向下
B.当x≥1时,y随x的增大而减小
C.当x=1时,y有最大值3
D.函数图象与x轴交于点(﹣1,0)和(3,0)
2、小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
3、二次函数y=(x+2)2+5的对称轴是( )
A.直线x= B.直线x=5 C.直线x=2 D.直线x=﹣2
4、二次函数y=ax2+bx+c(a≠0)的图象如图所示,与x轴交于点( 1,0)和(x,0),且1
5、抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
6、二次函数的图象如图所示,下列结论:①;②;③;④;⑤,⑥设,对应的函数值分别是,,则当时,其中正确结论序号为( )
A.①②③ B.①③⑥ C.①②⑥ D.③④⑤
7、如图,抛物线与轴交于点,对称轴为直线,则下列结论中正确的是( )
A.
B.当时,随的增大而增大
C.
D.是一元二次方程的一个根
8、若二次函数与轴的一个交点为,则代数式的值为( )
A. B. C. D.
9、二次函数的自变量与函数值的部分对应值如下表:
… -3 -2 -1 0 1 …
… -11 -3 1 1 -3 …
对于下列结论:①二次函数的图像开口向下;②当时,随的增大而减小;③二次函数的最大值是1;④若,是二次函数图像与轴交点的横坐标,则,其中,正确的是( )
A.①② B.③④ C.①③ D.①②④
10、已知二次函数的图象如图所示,对称轴为直线,下列结论中正确的是( )
A. B. C. D.
二、填空题(共 8 小题)
1、二次函数的图像如图所示,对称轴为直线,根据图中信息可求得该二次函数的解析式为______.
2、已知A(,),B(1,),C(4,)三点都在二次函数的图象上,则、、的大小关系为_______.
3、已知函数,当x______时,y随x的增大而减少.
4、一名男生推铅球,铅球行进的高度y(单位:米)与水平距离x(单位:米)之间的关系为,则这名男生这次推铅球的成绩是______米.
5、在东京奥运会跳水比赛中,中国小花全红婵的表现,令人印象深刻.在正常情况下,跳水运动员进行10米跳台训练时,必须在距水面5米之前完成规定的翻腾动作,并调整好入水姿势,否则容易出现失误.假设某运动员起跳后第t秒离水面的高度为h米,且.那么为了避免出现失误,这名运动员最多有_____秒时间,完成规定的翻腾动作.
6、在平面直角坐标系中,已知点,点,如果二次函数的图象与线段有交点,那么a的取值范围为__________.
7、二次函数y=ax2+bx+4的图象如图所示,则关于x的方程a(x+1)2+b(x+1)=﹣4的根为______.
8、某地的药材批发公司指导农民养植和销售某种药材,经市场调研发现1-8月份这种药材售价(元)与月份之间存在如下表所示的一次函数关系,同时,每千克的成本价(元)与月份之间近似满足如图所示的抛物线,观察两幅图表,试判断_____ 月份出售这种药材获利最大.
月份 ... 3 6 ...
每千克售价 ... 8 6 ...
三、解答题(共 6 小题)
1、如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),点P为抛物线上的一动点.
(1)求二次函数的解析式;
(2)如图,过点A作AC平行于x轴,交抛物线于点C,若点P在AC的上方,作PD平行于y轴交AB于点D,连接PA,PC,当S四边形APCD=时,求点P坐标;
(3)设抛物线的对称轴与AB交于点M,点Q在直线AB上,当以点M、E、P、Q为顶点的四边形为平行四边形时,请直接写出点Q的坐标.
2、如图,抛物线y=﹣x2+bx+c与x轴交于点B(1,0)点,与y轴交于点C(0,3),对称轴l与x轴交于点F,点E是直线AC上方抛物线上一动点,连接AE、EC.
(1)求抛物线的解析式;
(2)当四边形AECO面积最大时,求点E的坐标;
(3)在(2)的条件下,连接EF,点P是x轴上一动点,在抛物线上是否存在点Q,使得以F、E、P、Q为顶点的四边形是平行四边形.若存在,请直接写出点Q的坐标;若不存在,说明理由.
3、如图1,在平面直角坐标系中,抛物线与轴交于点和点,与轴交于点,经过点的直线与抛物线交于另一点,点为抛物线的顶点,抛物线的对称轴与轴交于点.
(1)求直线的解析式;
(2)如图2,点为直线上方抛物线上一动点,直线与轴交于点,连接,.当四边形的面积最大时,求点的坐标以及四边形面积的最大值.
(3)如图3,连接,将(1)中抛物线沿射线平移得到新抛物线,经过点,的顶点为点.在新抛物线上是否存在点,使得是以为直角边的直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
4、如图,抛物线y= x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,3),点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求抛物线的解析式,并写出此抛物线的对称轴和顶点坐标;
(2)如果以点P、N、B、O为顶点的四边形为平行四边形,求m的值;
(3)如果以B、P、N为顶点的三角形与△ABO相似,求点M的坐标.
5、实验表明,汽车急刹车的停车距离等于反应距离与制动距离之和;反应距离与汽车速度成正比,制动距离与汽车速度的平方成正比.已知当汽车的速度为时,急刹车的停车距离为;当汽车的速度为时,急刹车的停车距离为.设汽车的速度为,急刹车的停车距离为.
(1)求关于的函数表达式;
(2)一辆汽车以的速度行驶,突然发现正前方处有一障碍物,紧急刹车,问汽车与障碍物是否会相撞?并说明理由;
(3)一辆行驶中的汽车突然发现正前方处有一辆抛锚的危险用品运输车,紧急刹车,要使汽车距离运输车不小于处停住,则汽车行驶的最大速度是__________.
6、如图,在平面直角坐标系中,已知抛物线经过点A(2,0)和点,顶点为点D.
(1)求直线AB的表达式;
(2)求tan∠ABD的值;
(3)设线段BD与轴交于点P,如果点C在轴上,且与相似,求点C的坐标.
