不等式的解法(复习课)[上学期]
文档属性
| 名称 | 不等式的解法(复习课)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 34.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-18 08:24:00 | ||
图片预览



文档简介
课件9张PPT。不等式的解法一、常见不等式
1、一元一次不等式的法 2、绝对值不等式 x<-a或x>a-a<x<a|x|<a (a>0)|x|>a (a>0)ax>b 或 ax<b3、一元二次不等式的解法
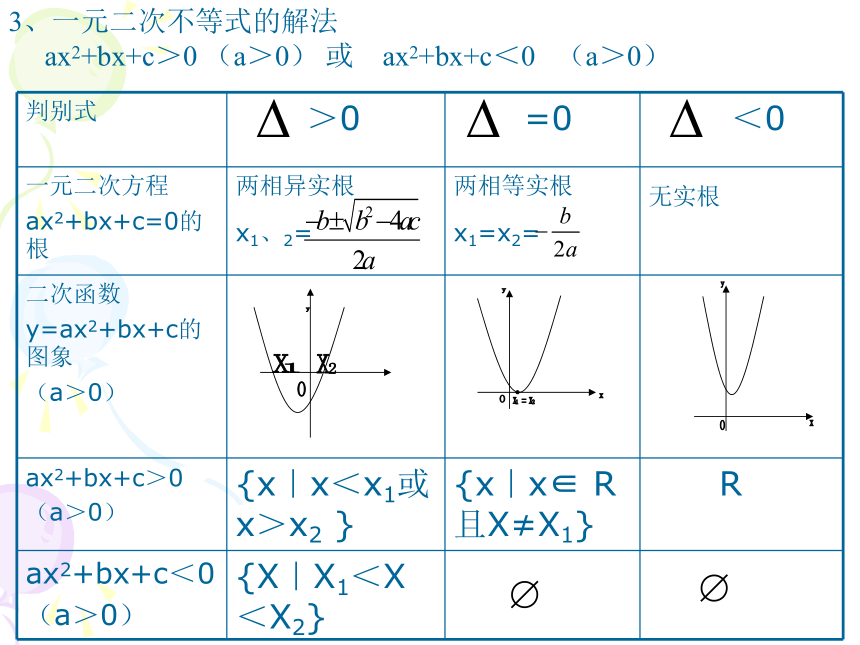
ax2+bx+c>0 (a>0) 或 ax2+bx+c<0 (a>0)
4、分式不等式的解法(1)简单分式不等式的解法 如:
(2)分式不等式的一般解法A≥0
B>0A≤0
B<0或A≥0
B<0或A≤0
B>0(3)数轴标根法—分式不等式—高次整式不等式
1、以后解不等式最后的结果都要写成集合或区间。
2、解不等式时一定要注意“是否有=”。
3、对绝对值不等式一定要分清是 “或”还是“且”,
是求并集还是要求交集。
4、对一元二次不等式,要注意二次项系数a是否大于0
5、数轴标根法—分式不等式—高次整式不等式
6、有关计算的要求------移项、去括号、通分、两边同
乘一个数是正还是负。
注意:二、应用举例:
1、解关于x的不等式:
ax+1<a2+x
2、已知a≠b,解关于的不等式:
a2x+b2(1-x) ≥[ax+b(1-x)]2
3、解关于x的不等式
x2-(a+a2)x+a3 >0
4、解关于x的不等式
( >a>b>0 )
5、解关于x的不等式:
ax2-2(a+1)x+4>0 (其中a≠0)
6、解不等式:
|x+3|-|x-5|>7
7、已知关于x的不等式 ax+b>0的解
集为 (1,+∞ ) ,解不等式
>0
1、含参数不等式要注意参数的范围、参数引起
的讨论
2、含两个绝对值不等式的解法
三、归纳总结:——零值点法
1、一元一次不等式的法 2、绝对值不等式 x<-a或x>a-a<x<a|x|<a (a>0)|x|>a (a>0)ax>b 或 ax<b3、一元二次不等式的解法
ax2+bx+c>0 (a>0) 或 ax2+bx+c<0 (a>0)
4、分式不等式的解法(1)简单分式不等式的解法 如:
(2)分式不等式的一般解法A≥0
B>0A≤0
B<0或A≥0
B<0或A≤0
B>0(3)数轴标根法—分式不等式—高次整式不等式
1、以后解不等式最后的结果都要写成集合或区间。
2、解不等式时一定要注意“是否有=”。
3、对绝对值不等式一定要分清是 “或”还是“且”,
是求并集还是要求交集。
4、对一元二次不等式,要注意二次项系数a是否大于0
5、数轴标根法—分式不等式—高次整式不等式
6、有关计算的要求------移项、去括号、通分、两边同
乘一个数是正还是负。
注意:二、应用举例:
1、解关于x的不等式:
ax+1<a2+x
2、已知a≠b,解关于的不等式:
a2x+b2(1-x) ≥[ax+b(1-x)]2
3、解关于x的不等式
x2-(a+a2)x+a3 >0
4、解关于x的不等式
( >a>b>0 )
5、解关于x的不等式:
ax2-2(a+1)x+4>0 (其中a≠0)
6、解不等式:
|x+3|-|x-5|>7
7、已知关于x的不等式 ax+b>0的解
集为 (1,+∞ ) ,解不等式
>0
1、含参数不等式要注意参数的范围、参数引起
的讨论
2、含两个绝对值不等式的解法
三、归纳总结:——零值点法
