数学归纳法及其应用举例[上学期]
文档属性
| 名称 | 数学归纳法及其应用举例[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 153.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-19 00:00:00 | ||
图片预览






文档简介
课件14张PPT。2.1 数学归纳法
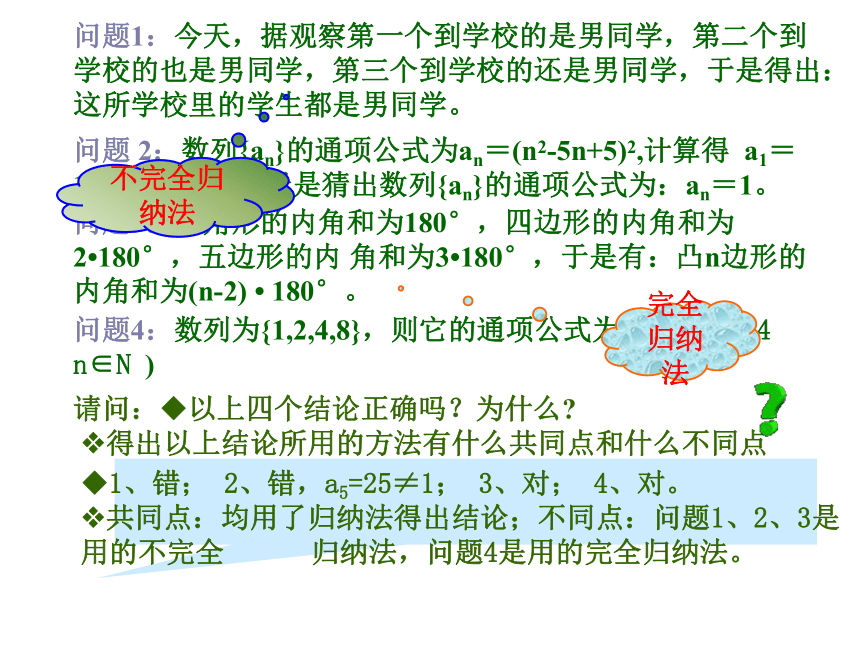
及其应用举例 请问:?以上四个结论正确吗?为什么?
?得出以上结论所用的方法有什么共同点和什么不同点问题4:数列为{1,2,4,8},则它的通项公式为an=2n-1(n≤4 n∈N ) ?1、错; 2、错,a5=25≠1; 3、对; 4、对。
?共同点:均用了归纳法得出结论;不同点:问题1、2、3是用的不完全 归纳法,问题4是用的完全归纳法。不完全归纳法完全归纳法2.1 数学归纳法及其应用举例课题引入 由一系列有限的特殊事例得出一般结论的推理方法,通常
叫做归纳法.2.1 数学归纳法及其应用举例新授课 1.在等差数列 中,已知首项为 ,公差为 , 2.1 数学归纳法及其应用举例新授课 对于由不完全归纳法得到的某些与自然数有关的数学命题我们常采用下面的方法来证明它们的正确性:先证明当n取第一个值n0(例如n0=1) 时命题成立,然后假设当n=k(k∈N,k≥n0)时命题成立证明当n=k+1时命题也成立,这种证明方法叫做数学归纳法.数学归纳法的两个步骤: (Ⅰ)证明当n=n0(n=1)(如n=1或2等)时,结论正确;(Ⅱ)假设n=k(k∈N*且k≥n0)时结论正确,并应用此假设证明n=k+1时结论也正确.注意:运用数学归纳法证题,以上两步缺一不可定 义2.1 数学归纳法及其应用举例新授课(2)假设当n=k时等式成立,就是那么这就是说,当n=k+1时,等式也成立由(1)和(2),可知的等式对任何 都成立.2.1 数学归纳法及其应用举例新授课数学归纳法证明一个与正整数有关命题的步骤是:(1)证明当 取第一个值 (如 或2等)时结论正确; (2)假设时 结论正确,证明
时结论也正确. 递推基础递推依据“找准起点,奠基要稳”“用上假设,递推才真”2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 【分析】①1+3+5…+(2n—1)=n当n分别取值1、2、3….k、k+1时的命题是什么?
n=1 命题:1=1n=2 命题:1+3=2 2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 【分析】(2) 第一步应做什么?本题的n0应取多少?n0=1, (3)在证传递性时,假设什么?求证什么?2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 证明: (1)当n=1时,左边=1,右边=1,等式成立.(2)假设当 时,等式成立,就是那么这就是说,当n=k+1时,等式也成立.由(1)和(2),可知的等式对任何 都成立.用数学归纳法证明:1、1+2+3+…+n=n(n+1)/2 (n∈N);证明:(1)当n=1时,左边=1,右边=1,等式是成立的。
(2)假设当n=k时等式成立,就是
1+2+3+…+k =k(k+1)/2
那么, 1+2+3+…+k+(k+1)= k(k+1)/2+ (k+1)
=(k+1)[(k+1)+1]/2
这就是说,当n=k+1时,等式也成立。因此,根据(1)和(2)可断定,等式对于任何n∈N都成立。练习:2、用数学归纳法证明:1+2+22+…+2n-1=2n-1 (n∈N*)证明:(1)当n=1时,左边=1,右边=1,等式是成立的。
(2)假设当n=k时等式成立,就是
1+2+22+…+2k-1 =2k-1
那么, 1+2+22+…+2k-1 +2k=2k-1 + 2k
=2×2k-1
=2k+1-1
这就是说,当n=k+1时,等式也成立。 因此,根据(1)和(2)可断定,等式对于任何n∈N*都成立。练习:①归纳法:由特殊到一般,是数学发现的重要方法;②数学归纳法的科学性:基础正确;可传递; ③数学归纳法证题程序化步骤:两个步骤,一个结论; ④数学归纳法优点:克服了完全归纳法的繁杂、不可行的缺点,又克服了不完全归纳法结论不可靠的不足,是一种科学方法,使我们认识到事情由简到繁、由特殊到一般、由有限到无穷. 数学归纳法的基本思想:
在可靠的基础上利用命题本身具有传递性,运用“有限”的手段来解决“无限”的问题数学归纳法的核心:
在验证命题n=n0正确的基础上,证明命题具有传递性,而第二步实际上是以一次逻辑的推理代替了无限的验证过程.所以说数学归纳法是一种合理、切实可行的科学证题方法,实现了有限到无限的飞跃。2.1 数学归纳法及其应用举例课堂小结2.1 数学归纳法及其应用举例练习.下面是某同学用数学归纳法证明命题
的过程.你认为他的证法正确吗?为什么?
(1).当n=1时,左边= , 右边=
(2).假设n=k时命题成立 即
那么n=k+1时,
左边
=右边,
即n=k+1时,命题也成立.
由(1)(2)知,对一切自然数,命题均正确.
及其应用举例 请问:?以上四个结论正确吗?为什么?
?得出以上结论所用的方法有什么共同点和什么不同点问题4:数列为{1,2,4,8},则它的通项公式为an=2n-1(n≤4 n∈N ) ?1、错; 2、错,a5=25≠1; 3、对; 4、对。
?共同点:均用了归纳法得出结论;不同点:问题1、2、3是用的不完全 归纳法,问题4是用的完全归纳法。不完全归纳法完全归纳法2.1 数学归纳法及其应用举例课题引入 由一系列有限的特殊事例得出一般结论的推理方法,通常
叫做归纳法.2.1 数学归纳法及其应用举例新授课 1.在等差数列 中,已知首项为 ,公差为 , 2.1 数学归纳法及其应用举例新授课 对于由不完全归纳法得到的某些与自然数有关的数学命题我们常采用下面的方法来证明它们的正确性:先证明当n取第一个值n0(例如n0=1) 时命题成立,然后假设当n=k(k∈N,k≥n0)时命题成立证明当n=k+1时命题也成立,这种证明方法叫做数学归纳法.数学归纳法的两个步骤: (Ⅰ)证明当n=n0(n=1)(如n=1或2等)时,结论正确;(Ⅱ)假设n=k(k∈N*且k≥n0)时结论正确,并应用此假设证明n=k+1时结论也正确.注意:运用数学归纳法证题,以上两步缺一不可定 义2.1 数学归纳法及其应用举例新授课(2)假设当n=k时等式成立,就是那么这就是说,当n=k+1时,等式也成立由(1)和(2),可知的等式对任何 都成立.2.1 数学归纳法及其应用举例新授课数学归纳法证明一个与正整数有关命题的步骤是:(1)证明当 取第一个值 (如 或2等)时结论正确; (2)假设时 结论正确,证明
时结论也正确. 递推基础递推依据“找准起点,奠基要稳”“用上假设,递推才真”2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 【分析】①1+3+5…+(2n—1)=n当n分别取值1、2、3….k、k+1时的命题是什么?
n=1 命题:1=1n=2 命题:1+3=2 2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 【分析】(2) 第一步应做什么?本题的n0应取多少?n0=1, (3)在证传递性时,假设什么?求证什么?2.1 数学归纳法及其应用举例例题讲解 例1 用数学归纳法证明 证明: (1)当n=1时,左边=1,右边=1,等式成立.(2)假设当 时,等式成立,就是那么这就是说,当n=k+1时,等式也成立.由(1)和(2),可知的等式对任何 都成立.用数学归纳法证明:1、1+2+3+…+n=n(n+1)/2 (n∈N);证明:(1)当n=1时,左边=1,右边=1,等式是成立的。
(2)假设当n=k时等式成立,就是
1+2+3+…+k =k(k+1)/2
那么, 1+2+3+…+k+(k+1)= k(k+1)/2+ (k+1)
=(k+1)[(k+1)+1]/2
这就是说,当n=k+1时,等式也成立。因此,根据(1)和(2)可断定,等式对于任何n∈N都成立。练习:2、用数学归纳法证明:1+2+22+…+2n-1=2n-1 (n∈N*)证明:(1)当n=1时,左边=1,右边=1,等式是成立的。
(2)假设当n=k时等式成立,就是
1+2+22+…+2k-1 =2k-1
那么, 1+2+22+…+2k-1 +2k=2k-1 + 2k
=2×2k-1
=2k+1-1
这就是说,当n=k+1时,等式也成立。 因此,根据(1)和(2)可断定,等式对于任何n∈N*都成立。练习:①归纳法:由特殊到一般,是数学发现的重要方法;②数学归纳法的科学性:基础正确;可传递; ③数学归纳法证题程序化步骤:两个步骤,一个结论; ④数学归纳法优点:克服了完全归纳法的繁杂、不可行的缺点,又克服了不完全归纳法结论不可靠的不足,是一种科学方法,使我们认识到事情由简到繁、由特殊到一般、由有限到无穷. 数学归纳法的基本思想:
在可靠的基础上利用命题本身具有传递性,运用“有限”的手段来解决“无限”的问题数学归纳法的核心:
在验证命题n=n0正确的基础上,证明命题具有传递性,而第二步实际上是以一次逻辑的推理代替了无限的验证过程.所以说数学归纳法是一种合理、切实可行的科学证题方法,实现了有限到无限的飞跃。2.1 数学归纳法及其应用举例课堂小结2.1 数学归纳法及其应用举例练习.下面是某同学用数学归纳法证明命题
的过程.你认为他的证法正确吗?为什么?
(1).当n=1时,左边= , 右边=
(2).假设n=k时命题成立 即
那么n=k+1时,
左边
=右边,
即n=k+1时,命题也成立.
由(1)(2)知,对一切自然数,命题均正确.
