17.1 勾股定理课件(共20张ppt)2022-2023学年八年级下学期数学人教版
文档属性
| 名称 | 17.1 勾股定理课件(共20张ppt)2022-2023学年八年级下学期数学人教版 |
|
|
| 格式 | pptx | ||
| 文件大小 | 528.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 00:00:00 | ||
图片预览





文档简介
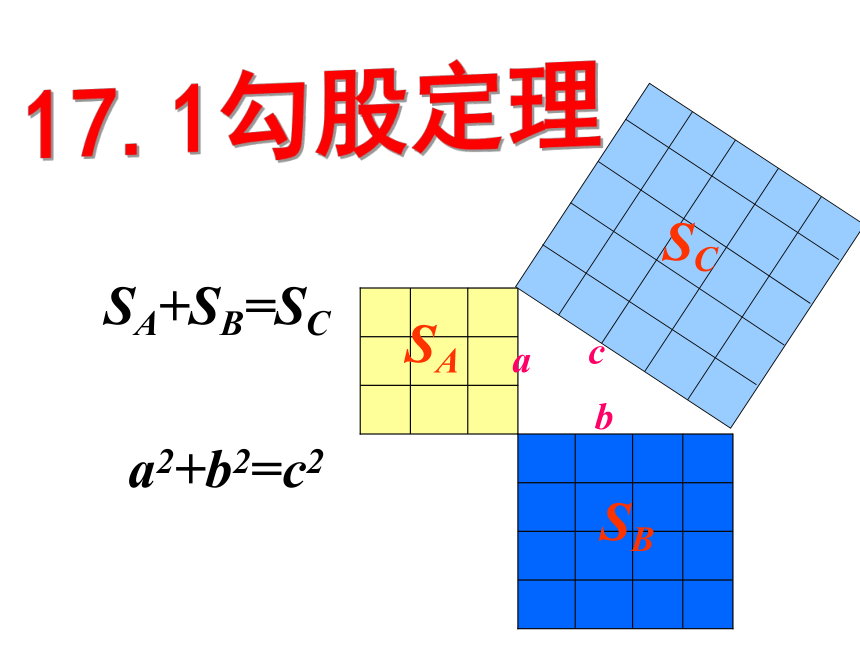
(共20张PPT)
SA+SB=SC
a2+b2=c2
a
b
c
SA
SB
SC
17.1勾股定理
a
b
c
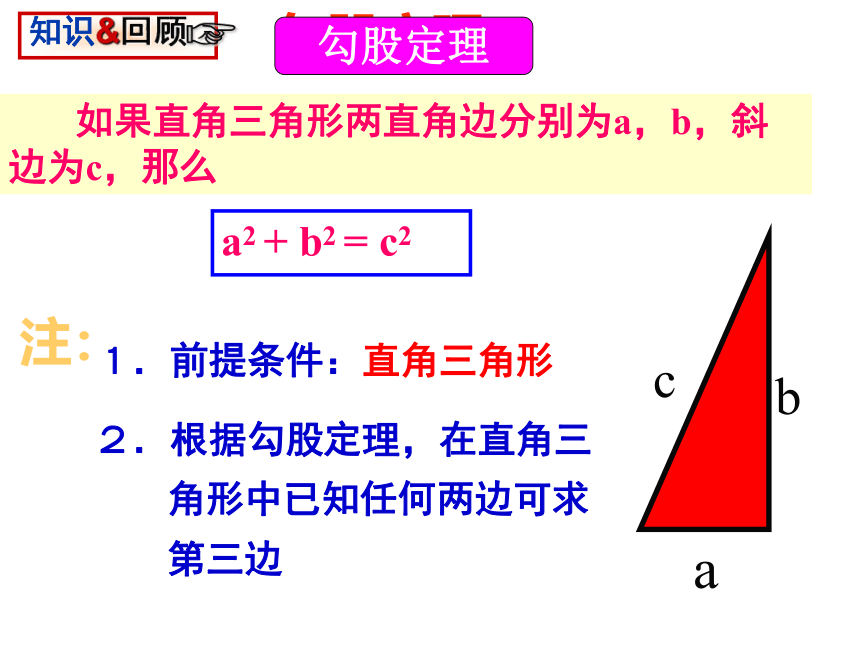
勾股定理
注:
1.前提条件:直角三角形
2.根据勾股定理,在直角三
角形中已知任何两边可求
第三边
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a
b
c
c2=a2 + b2
结论变形
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a2=c2 - b2
b2=c2 -a2
1. 在⊿ABC中, ∠C=900,
(1) 若a=8, b=6, 则 c=____,
(2) 若c=20, b=12, 则 a=___,
(3) 若c=13, a=5, 则b=____,
10
16
12
4. 在Rt⊿ABC中, 若a=3, b=4, 则
c=________.
5
2.在Rt△ABC中,∠C=900,a=2,c=5,则b=___.
3.在Rt△ABC中,∠B=900,a=3, b=4,则c=___.
一分二代三化简
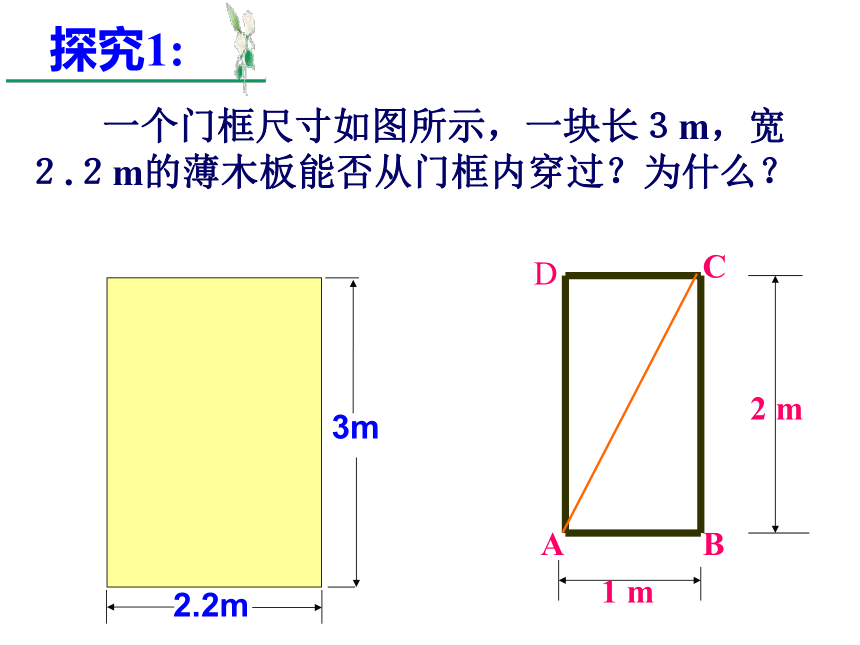
一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内穿过?为什么?
A
B
C
D
1 m
2 m
3m
2.2m
探究1:
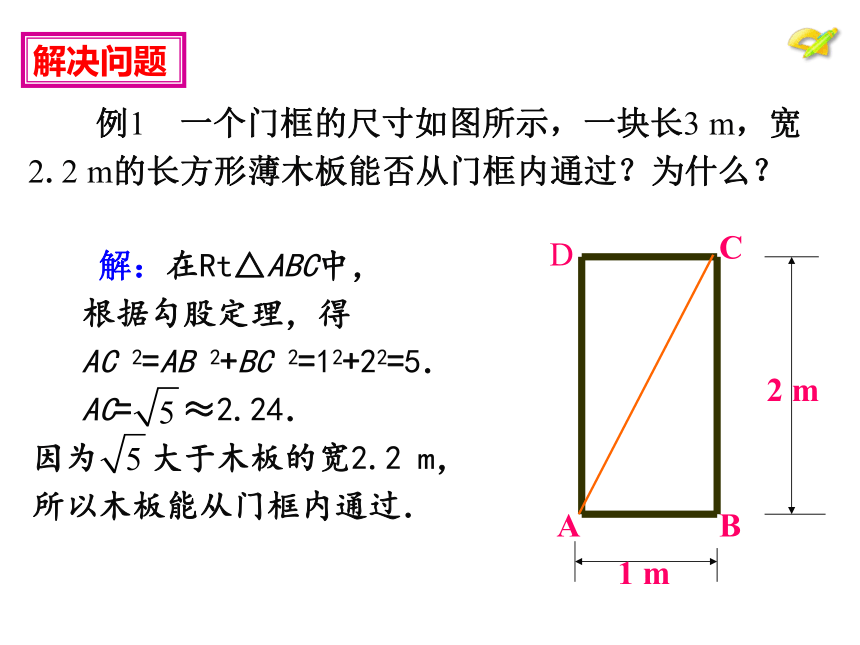
解决问题
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
根据勾股定理,得
AC 2=AB 2+BC 2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,
所以木板能从门框内通过.
A
B
C
D
1 m
2 m
(2)运用勾股定理解决生活中的一 些实际问题.
(1)将实际问题转化为数学问题, 建立数学模型.
归纳与小结
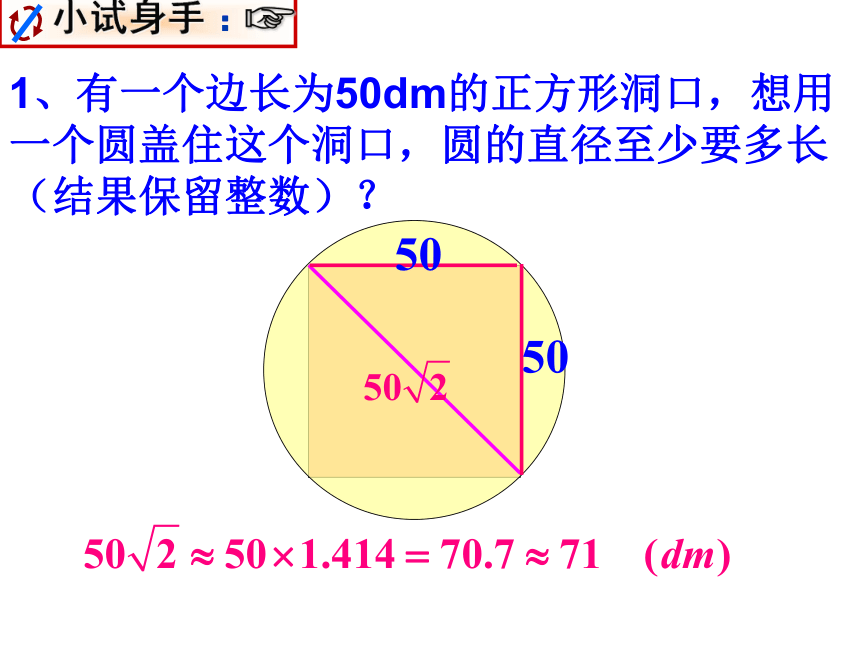
1、有一个边长为50dm的正方形洞口,想用一个圆盖住这个洞口,圆的直径至少要多长(结果保留整数)?
50
50
小试身手 :
2.一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 露出杯口外. (填“能”或“不能”)
4
10
能
拓展提高
4. 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
3.龙希想知道学校旗杆的高,她发现旗杆顶端的绳子垂到地面还多1米,当她把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮她算出来旗杆的高度吗?
A
B
C
5米
1米
拓展提高 形成技能
今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
B
C
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
拓展提高 形成技能
A
B
C
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
分析:
可设 AB=x, 则 AC=x+1,
有 AB2+BC2=AC2,
可列方程,
得 x2+52= ,
通过解方程可得.
拓展提高 形成技能
利用勾股定理解决实际问题的一般思路:
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型运用相应的数学知识;
(3)方程思想的运用.
A
C
O
B
D
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
3
2.5
0.5
2
3
分析:DB=OD-OB,求BD,可以 先求OB,OD.
A
C
O
B
D
梯子的顶端沿墙下滑0.5m,梯子底端外移_______.
在Rt△AOB中,
在Rt△COD中,
OD-OB = 2.236 -1.658 ≈0.58
0.58 m
一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
3
2.5
2
3
1.658
2.236
探究2:
A
C
O
B
D
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
思考:解完题后,小聪提出了如下两个问题,请你解答:
①如图1,在题中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
②若某人站在梯子的正中间P处(即梯子AB的中点),试问在梯子下滑过程中,请你在备用图中画出此人移动的路程(即点P移动的轨迹),并求出这个路程..
拓展提高 形成技能
利用勾股定理解决实际问题的一般思路:
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型运用相应的数学知识;
(3)方程思想的运用.
B
A
2、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m. 你能求出A、B两点间的距离吗(结果保留整数)?
C
60
20
小试身手 :
1、如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
1
2
3
拓展提高
SA+SB=SC
a2+b2=c2
a
b
c
SA
SB
SC
17.1勾股定理
a
b
c
勾股定理
注:
1.前提条件:直角三角形
2.根据勾股定理,在直角三
角形中已知任何两边可求
第三边
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a
b
c
c2=a2 + b2
结论变形
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a2=c2 - b2
b2=c2 -a2
1. 在⊿ABC中, ∠C=900,
(1) 若a=8, b=6, 则 c=____,
(2) 若c=20, b=12, 则 a=___,
(3) 若c=13, a=5, 则b=____,
10
16
12
4. 在Rt⊿ABC中, 若a=3, b=4, 则
c=________.
5
2.在Rt△ABC中,∠C=900,a=2,c=5,则b=___.
3.在Rt△ABC中,∠B=900,a=3, b=4,则c=___.
一分二代三化简
一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内穿过?为什么?
A
B
C
D
1 m
2 m
3m
2.2m
探究1:
解决问题
例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
根据勾股定理,得
AC 2=AB 2+BC 2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,
所以木板能从门框内通过.
A
B
C
D
1 m
2 m
(2)运用勾股定理解决生活中的一 些实际问题.
(1)将实际问题转化为数学问题, 建立数学模型.
归纳与小结
1、有一个边长为50dm的正方形洞口,想用一个圆盖住这个洞口,圆的直径至少要多长(结果保留整数)?
50
50
小试身手 :
2.一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 露出杯口外. (填“能”或“不能”)
4
10
能
拓展提高
4. 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
3.龙希想知道学校旗杆的高,她发现旗杆顶端的绳子垂到地面还多1米,当她把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮她算出来旗杆的高度吗?
A
B
C
5米
1米
拓展提高 形成技能
今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐.问水深、葭长各几何?
A
B
C
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
拓展提高 形成技能
A
B
C
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
分析:
可设 AB=x, 则 AC=x+1,
有 AB2+BC2=AC2,
可列方程,
得 x2+52= ,
通过解方程可得.
拓展提高 形成技能
利用勾股定理解决实际问题的一般思路:
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型运用相应的数学知识;
(3)方程思想的运用.
A
C
O
B
D
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
3
2.5
0.5
2
3
分析:DB=OD-OB,求BD,可以 先求OB,OD.
A
C
O
B
D
梯子的顶端沿墙下滑0.5m,梯子底端外移_______.
在Rt△AOB中,
在Rt△COD中,
OD-OB = 2.236 -1.658 ≈0.58
0.58 m
一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
3
2.5
2
3
1.658
2.236
探究2:
A
C
O
B
D
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
思考:解完题后,小聪提出了如下两个问题,请你解答:
①如图1,在题中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
②若某人站在梯子的正中间P处(即梯子AB的中点),试问在梯子下滑过程中,请你在备用图中画出此人移动的路程(即点P移动的轨迹),并求出这个路程..
拓展提高 形成技能
利用勾股定理解决实际问题的一般思路:
(1)重视对实际问题题意的正确理解;
(2)建立对应的数学模型运用相应的数学知识;
(3)方程思想的运用.
B
A
2、如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m. 你能求出A、B两点间的距离吗(结果保留整数)?
C
60
20
小试身手 :
1、如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
1
2
3
拓展提高
