17.1勾股定理的应用课件(共24张ppt)2022-2023学年八年级下学期数学人教版
文档属性
| 名称 | 17.1勾股定理的应用课件(共24张ppt)2022-2023学年八年级下学期数学人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 16:30:50 | ||
图片预览


文档简介
(共24张PPT)
17.1勾股定理的应用
人教版八年级(下)第十七章
周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?”
商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形‘矩’得到的一条直角边‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜边‘弦’就必定是5。”
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:
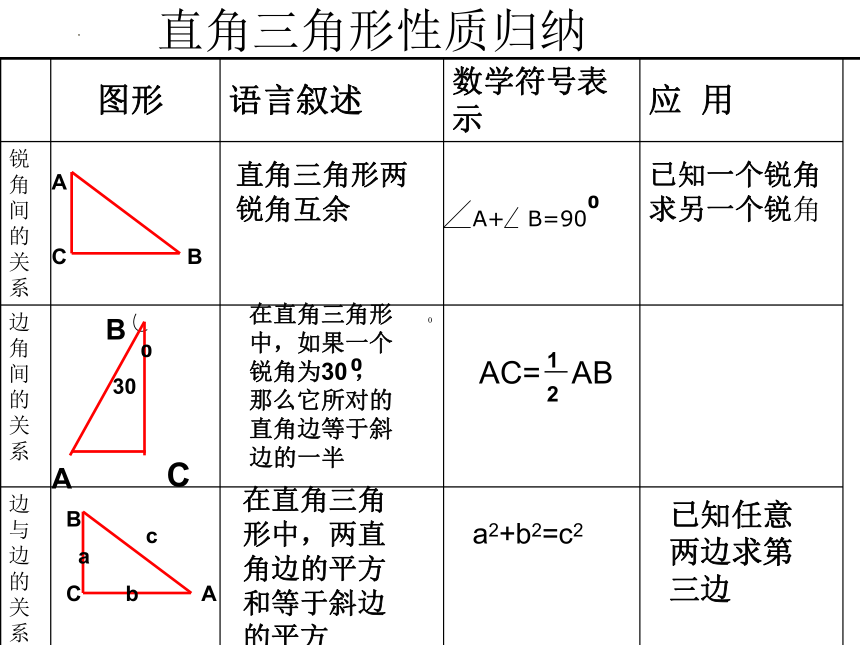
直角三角形性质归纳
图形 语言叙述 数学符号表示 应 用
锐角间的关系 边角间的关系 边与边的关系
A
C
B
30
0
A
C
B
B
C
A
b
c
a
直角三角形两锐角互余
0
在直角三角形中,如果一个锐角为30 ,那么它所对的直角边等于斜边的一半
在直角三角形中,两直角边的平方和等于斜边的平方
0
A+ B=90
1
2
AC=-AB
已知一个锐角求另一个锐角
已知任意两边求第三边
a2+b2=c2
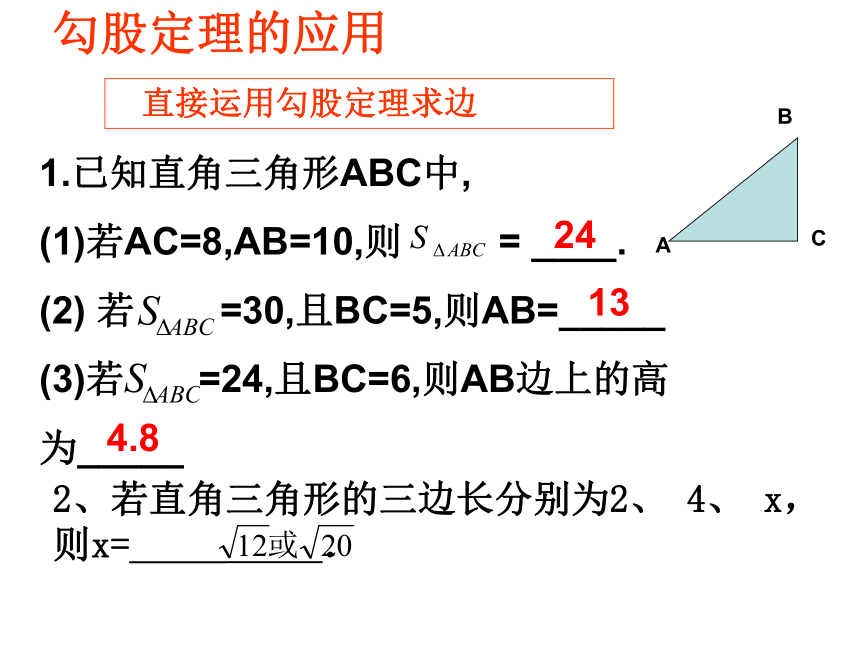
勾股定理的应用
直接运用勾股定理求边
2、若直角三角形的三边长分别为2、 4、 x,则x=_____ .
1.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____
B
A
C
24
13
4.8
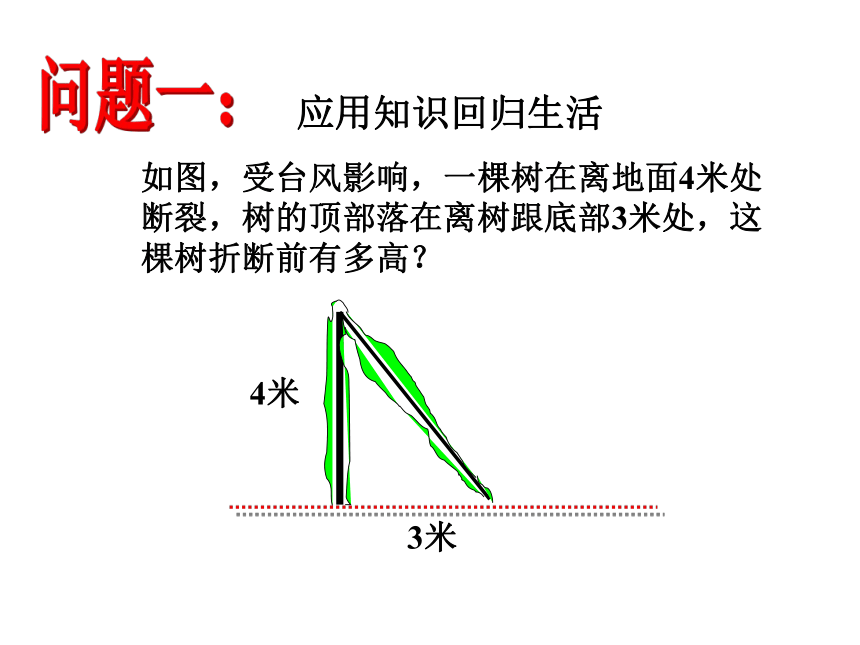
如图,受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
应用知识回归生活
4米
3米
问题一:
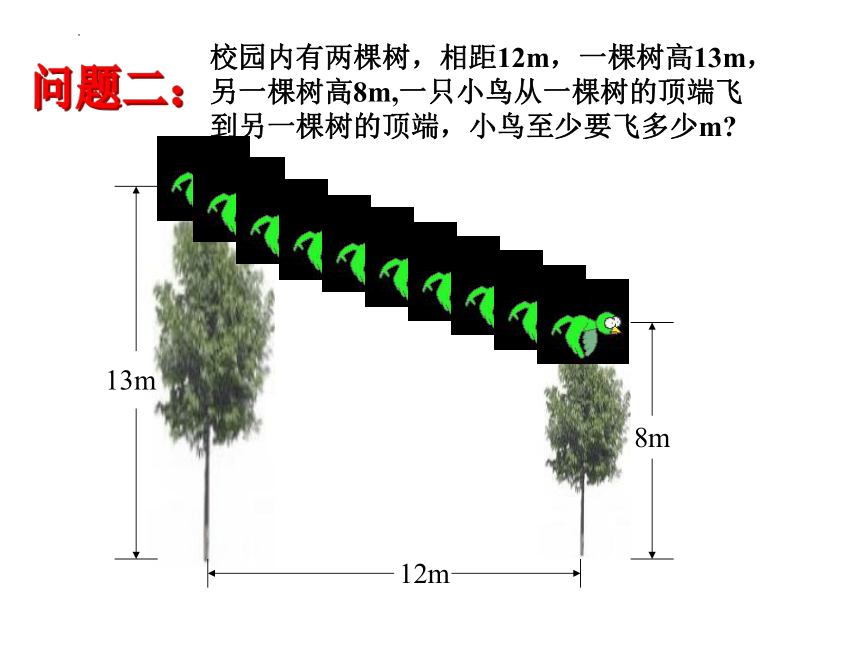
13m
12m
8m
校园内有两棵树,相距12m,一棵树高13m,另一棵树高8m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少m
问题二:
13m
12m
8m
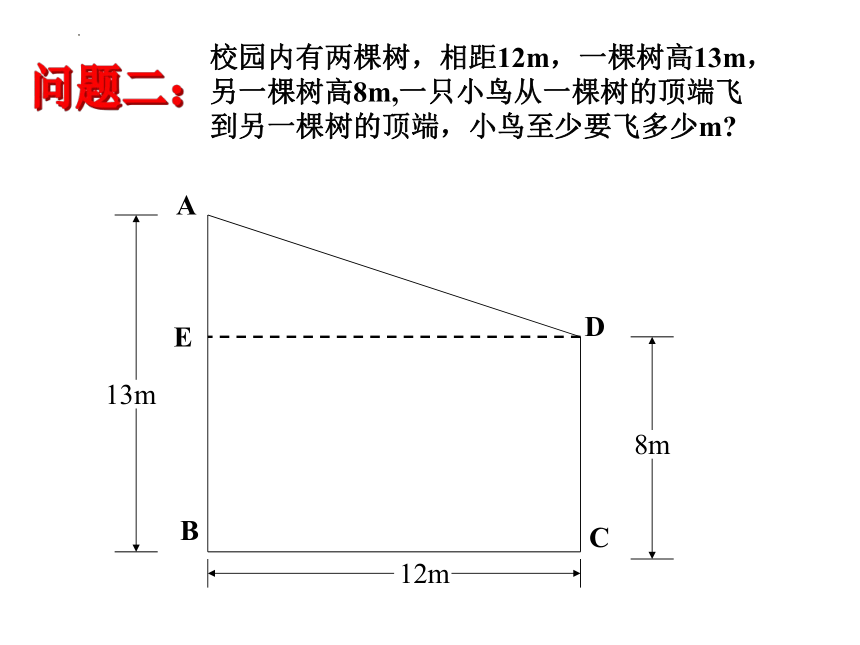
A
B
C
D
校园内有两棵树,相距12m,一棵树高13m,另一棵树高8m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少m
问题二:
E
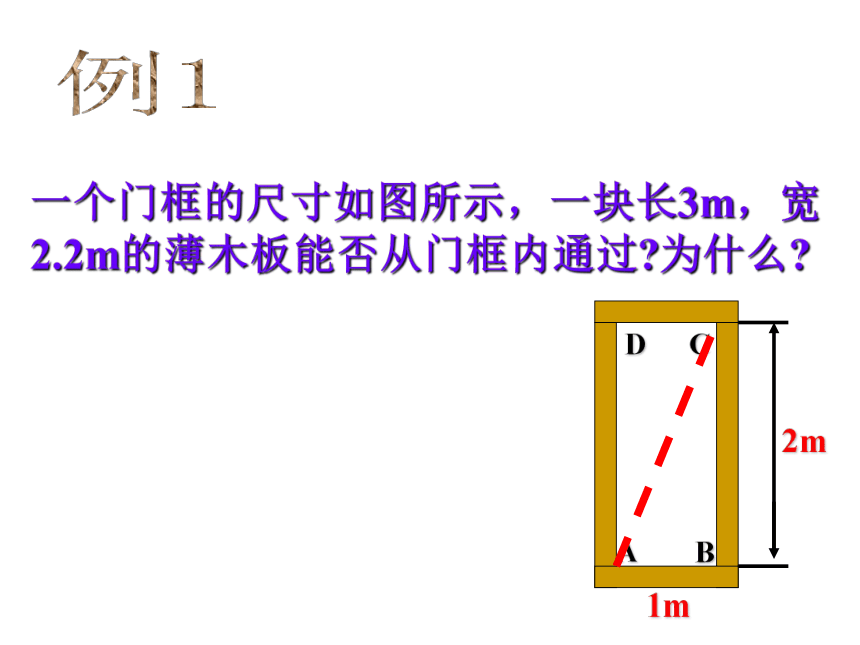
例1
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
1m
跟踪练习:教科书第26页练习1.2.
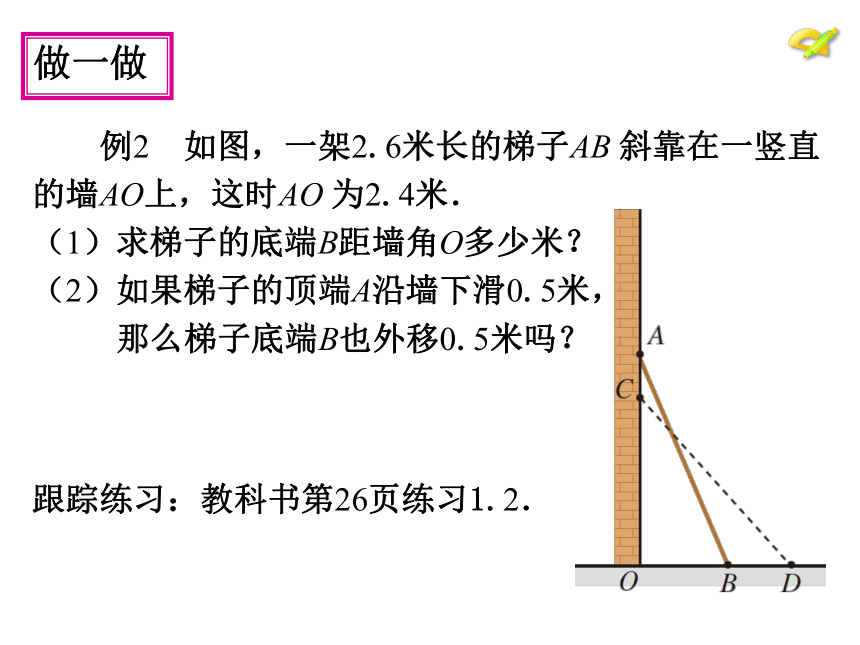
做一做
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?
试一试
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
x2 + 52 = (x+1)2
x = 12
水池
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
x2+42=(8-x)2
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
探究3
数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?
0
1
2
3
4
解:
L
A
B
试
一
试
1请你在作业纸上画图,在数轴上表示 的点
2请同学们归纳出如何在数轴上画出表示 的点的方法?
3你能在数轴上表示 的点吗?试一试!
扩展
利用勾股定理作出长为
的线段.
1
1
用同样的方法,你能否在数轴上画出表示
,…
0
2
1
3
5
4
1
圆柱(锥)中的最值问题
例3、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
长方体中的最值问题
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
聪明的葛藤
有一个人拿一根杆子进城,横着拿不能
进,竖着拿也不能进,干脆将其折断,
才解决了问题。
古代笑话一则
学生活动
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是4尺、3尺、12尺,那么,你能帮小明估计一下买的竹竿至多是多少尺吗?(结果取整数)
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边
求第三边
抽象
归类
解决
建构活动
17.1勾股定理的应用
人教版八年级(下)第十七章
周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?”
商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形‘矩’得到的一条直角边‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜边‘弦’就必定是5。”
中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:
直角三角形性质归纳
图形 语言叙述 数学符号表示 应 用
锐角间的关系 边角间的关系 边与边的关系
A
C
B
30
0
A
C
B
B
C
A
b
c
a
直角三角形两锐角互余
0
在直角三角形中,如果一个锐角为30 ,那么它所对的直角边等于斜边的一半
在直角三角形中,两直角边的平方和等于斜边的平方
0
A+ B=90
1
2
AC=-AB
已知一个锐角求另一个锐角
已知任意两边求第三边
a2+b2=c2
勾股定理的应用
直接运用勾股定理求边
2、若直角三角形的三边长分别为2、 4、 x,则x=_____ .
1.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____
B
A
C
24
13
4.8
如图,受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
应用知识回归生活
4米
3米
问题一:
13m
12m
8m
校园内有两棵树,相距12m,一棵树高13m,另一棵树高8m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少m
问题二:
13m
12m
8m
A
B
C
D
校园内有两棵树,相距12m,一棵树高13m,另一棵树高8m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少m
问题二:
E
例1
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
1m
跟踪练习:教科书第26页练习1.2.
做一做
例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?
试一试
有一个水池,水面是一个边长为10尺的正方形,在
水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根
芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池
的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
x2 + 52 = (x+1)2
x = 12
水池
如图,折叠长方形(四个角都是直角,对边相等)的一边,使点D落在BC边上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长
(2)求EC的长.
问题与思考
10
4
6
8
10
x
E
F
D
C
B
A
8-x
8-x
x2+42=(8-x)2
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
探究3
数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?
0
1
2
3
4
解:
L
A
B
试
一
试
1请你在作业纸上画图,在数轴上表示 的点
2请同学们归纳出如何在数轴上画出表示 的点的方法?
3你能在数轴上表示 的点吗?试一试!
扩展
利用勾股定理作出长为
的线段.
1
1
用同样的方法,你能否在数轴上画出表示
,…
0
2
1
3
5
4
1
圆柱(锥)中的最值问题
例3、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
B
A
C
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
长方体中的最值问题
聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。
(1)
(2)
数学奇闻
有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)
A
B
C
20尺
3×7=21(尺)
聪明的葛藤
有一个人拿一根杆子进城,横着拿不能
进,竖着拿也不能进,干脆将其折断,
才解决了问题。
古代笑话一则
学生活动
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是4尺、3尺、12尺,那么,你能帮小明估计一下买的竹竿至多是多少尺吗?(结果取整数)
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边
求第三边
抽象
归类
解决
建构活动
