人教版七年级下册数学5.2.2平行线的判断课时练习题(含答案)
文档属性
| 名称 | 人教版七年级下册数学5.2.2平行线的判断课时练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-08 16:37:07 | ||
图片预览

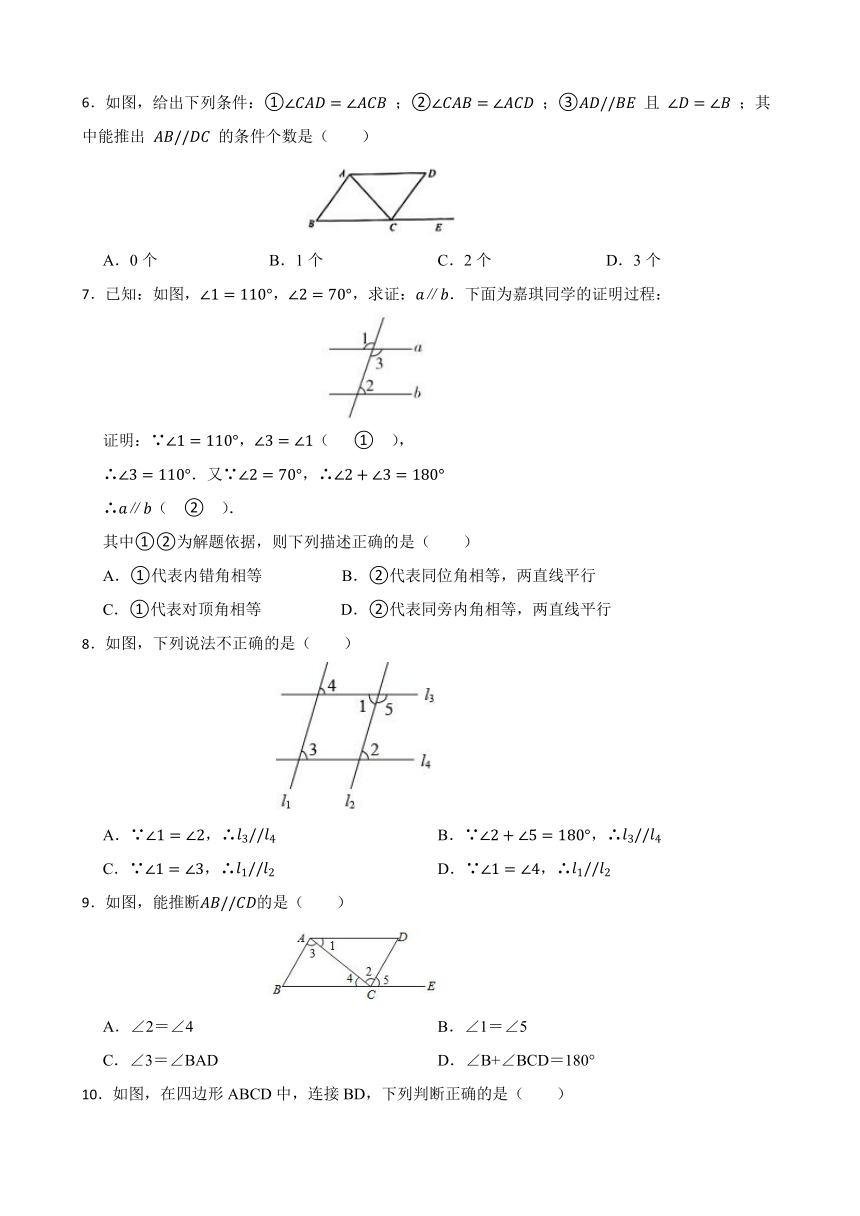
文档简介
初中数学试卷2023年01月02日
一、单选题
1.将一块直角三角板ABC按如图方式放置,其中∠ABC=30°,A、B两点分别落在直线m、n上,∠1=20°,添加下列哪一个条件可使直线m∥n( )
A.∠2=20° B.∠2=30° C.∠2=45° D.∠2=50°
2.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4 B.∠4=∠5
C.∠1=∠3 D.∠1+∠4=180°
3.如图,下列条件能判定 的是( )
A. B.
C. D. 且
4.如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠1=∠A B.∠A=∠3
C.∠1=∠4 D.∠A+∠2=180°
5.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD B.AD∥BC C.AD=BC D.AB=CD
6.如图,给出下列条件:① ;② ;③ 且 ;其中能推出 的条件个数是( )
A.0个 B.1个 C.2个 D.3个
7.已知:如图,,,求证:∥.下面为嘉琪同学的证明过程:
证明:∵,( ① ),
∴.又∵,∴
∴∥( ② ).
其中①②为解题依据,则下列描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
8.如图,下列说法不正确的是( )
A.∵,∴ B.∵,∴
C.∵,∴ D.∵,∴
9.如图,能推断的是( )
A.∠2=∠4 B.∠1=∠5
C.∠3=∠BAD D.∠B+∠BCD=180°
10.如图,在四边形ABCD中,连接BD,下列判断正确的是( )
A.若∠1=∠2,则AB//CD
B.若∠3=∠4,则AD//BC
C.若∠A+∠ABC=180°,则AB//CD
D.若∠A=∠C,∠ABC=∠ADC,则AB//CD
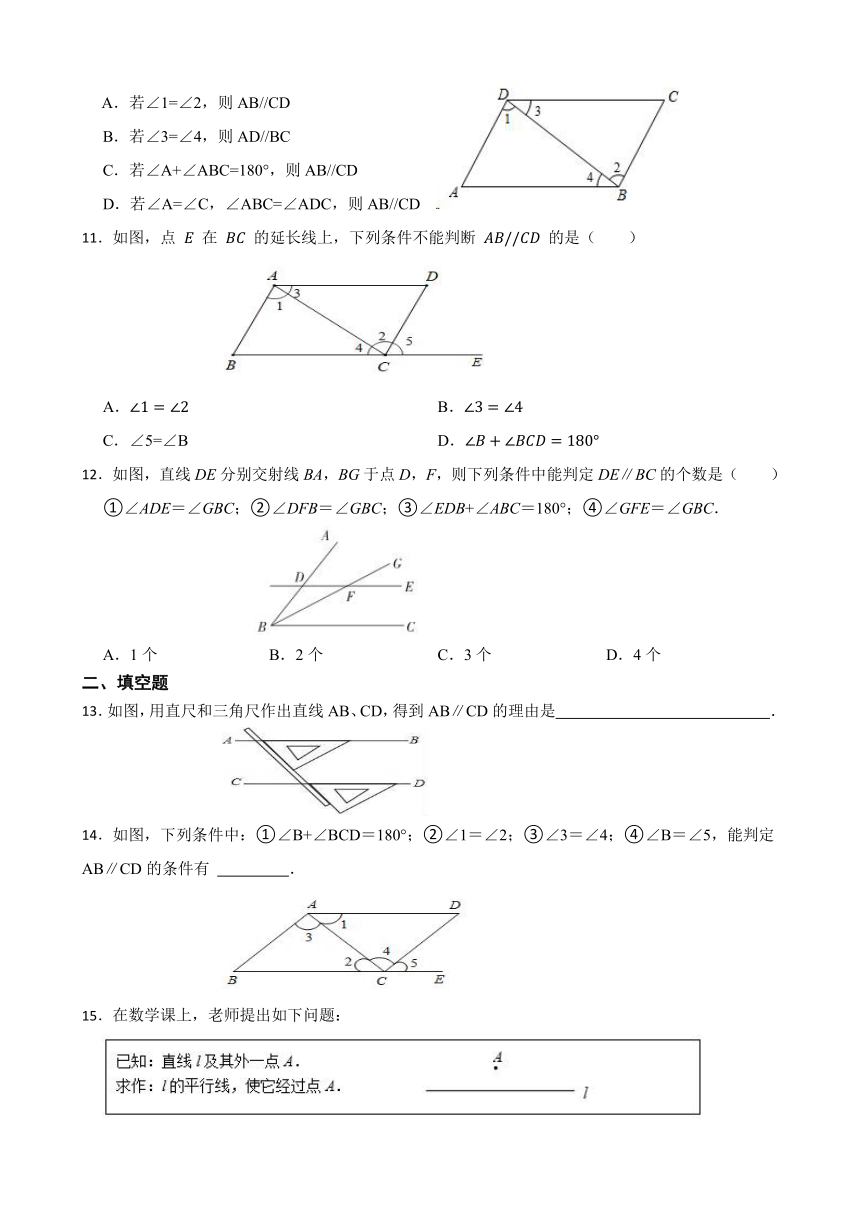
11.如图,点 在 的延长线上,下列条件不能判断 的是( )
A. B.
C.∠5=∠B D.
12.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的个数是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .
14.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 .
15.在数学课上,老师提出如下问题:
小菲用两块形状、大小相同的三角尺完成了该题的作图,作法如下:
老师说:“小菲的作法正确.”
请回答:小菲的作图的依据是 .
16.如图,不添加辅助线,请添加一个能判定 的条件: .
17.用两个相同的三角板如图所示摆放,直线a∥b,画图依据是: .
18.如图,下列条件中:①;②;③;④;⑤.则一定能判定的条件有 (填写所有正确的序号).
19.如图,已知直线c与a,b均相交,若直线a∥b需要添加条件
20.如图,添加一个你认为合适的条件 使 .
21.如图,点E在AC的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有 个.
22.如图,请你添加一个条件,使 AB∥CD,这个条件是 .
三、作图题
23.如图,已知 ,点 是 边上的一点.
(1)在 的右侧作 (用尺规作图法,保留作图痕迹,不写作法);
(2)在(1)的条件下,判断直线 与直线 的位置关系,并说明理由.
四、解答题
24.如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
25.如图所示,已知,.求证.
26.如图直角三角形ABC中, , 平分 , ,求证: .
答案
1.D 2.C 3.D 4.A 5.B 6.C 7.C 8.C 9.D 10.D 11.B 12.C
13.同位角相等,两直线平行 14.①③④ 15.内错角相等,两直线平行
16.∠ADE=∠B 17.内错角相等,两直线平行 18.①③⑤ 19.∠1=∠4(答案不唯一)
20.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
21.3 22.∠CDA=∠DAB
23.(1)解: 如图, 就是所要求作的角
(2)解: 直线 与直线 的位置关系为:
理由如下:
由(1)作图可得: ,
∴ .
24.解:AD∥BE,
理由是:∵AB∥CD,
∴∠1=∠ACD,
∵∠3=∠E+∠CAF,∠4=∠ACD+∠CAF,∠3=∠4,
∴∠1=∠E=∠ACD,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE.
25.证明:∵
∴(两直线平行,同位角相等)
又∵
∴
∴(内错角相等,两直线平行)-
26.证明: 为直角三角形且 ,
,
∵ 平分 ,
,
且 ,
∴∠EAD+∠CAF=180°-∠CAB=90°
∴
,
,
∴CE∥FD.
一、单选题
1.将一块直角三角板ABC按如图方式放置,其中∠ABC=30°,A、B两点分别落在直线m、n上,∠1=20°,添加下列哪一个条件可使直线m∥n( )
A.∠2=20° B.∠2=30° C.∠2=45° D.∠2=50°
2.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( )
A.∠2=∠4 B.∠4=∠5
C.∠1=∠3 D.∠1+∠4=180°
3.如图,下列条件能判定 的是( )
A. B.
C. D. 且
4.如图,在下列给出的条件中,不能判定AB∥DF的是( )
A.∠1=∠A B.∠A=∠3
C.∠1=∠4 D.∠A+∠2=180°
5.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD B.AD∥BC C.AD=BC D.AB=CD
6.如图,给出下列条件:① ;② ;③ 且 ;其中能推出 的条件个数是( )
A.0个 B.1个 C.2个 D.3个
7.已知:如图,,,求证:∥.下面为嘉琪同学的证明过程:
证明:∵,( ① ),
∴.又∵,∴
∴∥( ② ).
其中①②为解题依据,则下列描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
8.如图,下列说法不正确的是( )
A.∵,∴ B.∵,∴
C.∵,∴ D.∵,∴
9.如图,能推断的是( )
A.∠2=∠4 B.∠1=∠5
C.∠3=∠BAD D.∠B+∠BCD=180°
10.如图,在四边形ABCD中,连接BD,下列判断正确的是( )
A.若∠1=∠2,则AB//CD
B.若∠3=∠4,则AD//BC
C.若∠A+∠ABC=180°,则AB//CD
D.若∠A=∠C,∠ABC=∠ADC,则AB//CD
11.如图,点 在 的延长线上,下列条件不能判断 的是( )
A. B.
C.∠5=∠B D.
12.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的个数是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .
14.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 .
15.在数学课上,老师提出如下问题:
小菲用两块形状、大小相同的三角尺完成了该题的作图,作法如下:
老师说:“小菲的作法正确.”
请回答:小菲的作图的依据是 .
16.如图,不添加辅助线,请添加一个能判定 的条件: .
17.用两个相同的三角板如图所示摆放,直线a∥b,画图依据是: .
18.如图,下列条件中:①;②;③;④;⑤.则一定能判定的条件有 (填写所有正确的序号).
19.如图,已知直线c与a,b均相交,若直线a∥b需要添加条件
20.如图,添加一个你认为合适的条件 使 .
21.如图,点E在AC的延长线上,对于给出的四个条件:(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有 个.
22.如图,请你添加一个条件,使 AB∥CD,这个条件是 .
三、作图题
23.如图,已知 ,点 是 边上的一点.
(1)在 的右侧作 (用尺规作图法,保留作图痕迹,不写作法);
(2)在(1)的条件下,判断直线 与直线 的位置关系,并说明理由.
四、解答题
24.如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
25.如图所示,已知,.求证.
26.如图直角三角形ABC中, , 平分 , ,求证: .
答案
1.D 2.C 3.D 4.A 5.B 6.C 7.C 8.C 9.D 10.D 11.B 12.C
13.同位角相等,两直线平行 14.①③④ 15.内错角相等,两直线平行
16.∠ADE=∠B 17.内错角相等,两直线平行 18.①③⑤ 19.∠1=∠4(答案不唯一)
20.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
21.3 22.∠CDA=∠DAB
23.(1)解: 如图, 就是所要求作的角
(2)解: 直线 与直线 的位置关系为:
理由如下:
由(1)作图可得: ,
∴ .
24.解:AD∥BE,
理由是:∵AB∥CD,
∴∠1=∠ACD,
∵∠3=∠E+∠CAF,∠4=∠ACD+∠CAF,∠3=∠4,
∴∠1=∠E=∠ACD,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE.
25.证明:∵
∴(两直线平行,同位角相等)
又∵
∴
∴(内错角相等,两直线平行)-
26.证明: 为直角三角形且 ,
,
∵ 平分 ,
,
且 ,
∴∠EAD+∠CAF=180°-∠CAB=90°
∴
,
,
∴CE∥FD.
