江苏 简单的线性规划问题[下学期]

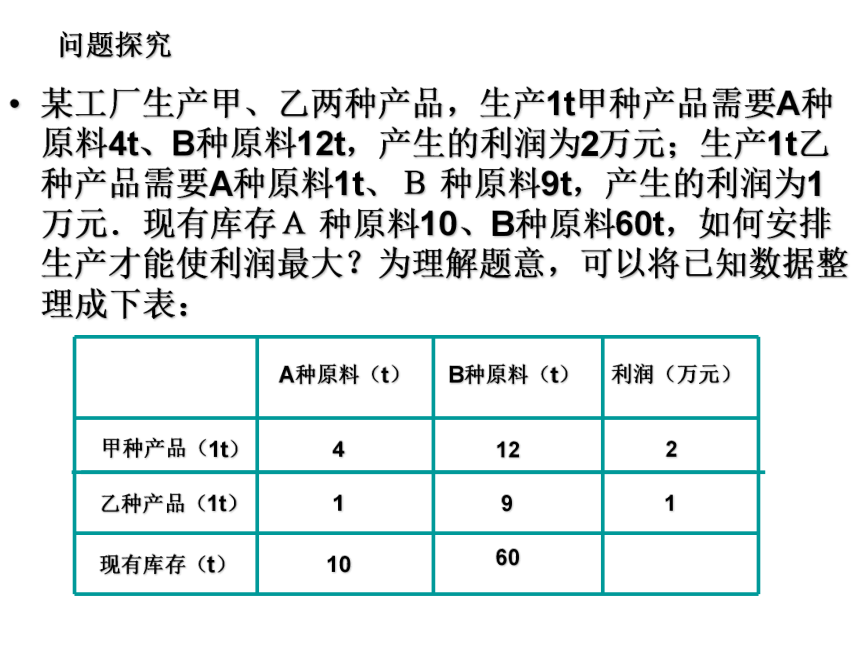
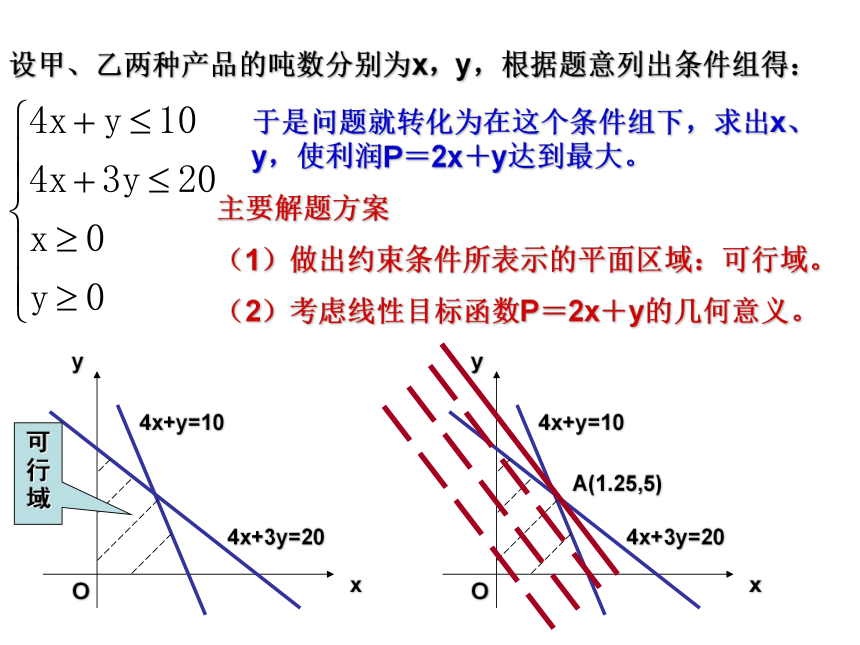
课件9张PPT。简单的线性规划问题问题探讨在实际应用中，经常会遇到：“如何安排生产，才能使利润最大”或“怎样设计，才能使安排最合理？”等等的问题。条件式是等式，我们只需要消去y或x，就可以转化为一元函数的最值问题。但如果条件是不等式(组)，则无法通过消元的方法达成消元的目的，这时就需要另想办法来解决这个问题，这就是我们本节课要学习的方法：线性规划问题探究某工厂生产甲、乙两种产品，生产1t甲种产品需要A种原料4t、B种原料12t，产生的利润为2万元；生产1t乙种产品需要A种原料1t、Ｂ 种原料9t，产生的利润为1万元．现有库存Ａ 种原料10、B种原料60t，如何安排生产才能使利润最大？为理解题意，可以将已知数据整理成下表：设甲、乙两种产品的吨数分别为x，y，根据题意列出条件组得：于是问题就转化为在这个条件组下，求出x、y，使利润P＝2x＋y达到最大。主要解题方案
（1）做出约束条件所表示的平面区域：可行域。
（2）考虑线性目标函数P＝2x＋y的几何意义。4x+y=104x+3y=20xyO可行域4x+y=104x+3y=20xyOA(1.25,5)几个重要的概念1、约束条件；
2、线性目标函数；
3、可行域；
4、最优解。通过上述例题的过程，需要掌握：
1、怎样根据已知列出约束条件：将已知条件列表。
2、写出线性目标函数。
3、P的几何意义的理解：直线在y轴上的截距和P的最值关系。
4、判断并求出最优解：通常是边界直线交点的坐标；难点是线性目标函数所在的直线和边界直线之间的关系。
5、写出最值。总结与提升这类求线性目标函数在线性约束条件下的最大值或最小值的问题，通常称为线性规划问题．
上述只含有两个变量的简单线性规划问题可用图解法来解决．
线性规划是一种重要的优化模型，生产实际中有许多问题都可以归结为线性规划问题．例1.投资生产A产品时，每生产一百吨需要资金200万元，需场地200ｍ2，可获利润300万元；投资生产B产品时，每生产一百米需要资金300万元，需场地100ｍ2，可获利润200万元．现某单位可使用资金1400万元，场地900ｍ2，问：应作怎样的组合投资，可使获利最大？例2.某运输公司向某地区运送物资，每天至少运送180t．该公司有8辆载重为6t的A型卡车与4辆载重为10t的B型卡车，有10名驾驶员．每辆卡车每天往返次数为A型车４次，B型车3次．每辆卡车每天往返的成本费A型车为320元，B型车为504元．试为该公司设计调配车辆方案，使公司花费的成本最低．请同学们整理条件，列出表格，写出约束条件和线性目标函数思考：怎样寻找可行域中的整数点，并找出其最优解巩固与练习 一家饮料厂商专营甲、乙两种果汁饮料，甲种饮料的主要配方是每3份李子汁加１份苹果汁，乙种饮料的配方是李子汁和苹果汁各一半．该厂每天能获得的原料是2000L李子汁和1000L苹果汁，又厂方的利润是1L甲种饮料得3元,1L乙种饮料得4元．那么厂方每天生产甲、乙两种饮料各多少，才能获利最大？